Oran
En az biri sıfırdan farklı ve birimleri aynı olan iki çokluğun birbirine bölümüne (karşılaştırılmasına) oran denir. a nın b ye oranı veya a:b şeklinde gösterilir.
Orantı
İki veya daha fazla oranın eşitliğine orantı denir.
eşitliği bir orantı belirtir ve “a değerinin b değerine oranı, c değerinin d değerine oranına eşittir.” şeklinde okunur.
Sabit bir k değeri için eşitliğindeki k değerine oran sabiti denir.
orantısı, a : b = c : d şeklinde de yazılabilir. Bu orantıda b ve c ye içler, a ve d ye dışlar denir.
Orantının Özellikleri
- İçler çarpımı dışlar çarpımına eşittir.
- Bir orantıda içler veya dışlar kendi arasında yer değiştirebilir. Bu durumda oranlar değişse bile orantının eşitliği değişmez. veya olabilir.
- Paylar ve paydalar kendi arasında toplanır ya da çıkarılır ise orantı sabiti değişmez. olur.
- m ve n sıfırdan farklı birer reel sayı olmak üzere
- ve olur.
- ise olur.
- ise, a=b.k, c=b.k, e=f.k dir.
Orantı Çeşitleri
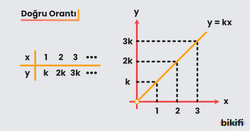
Doğru Orantı
İki çokluktan biri artarken diğeri de aynı oranda artıyorsa veya biri azalırken diğeri de aynı oranda azalıyor ise bu iki çokluk doğru orantılıdır veya kısaca orantılıdır denir. Doğru orantılı iki çokluğun oranı sabittir.
y ile x doğru orantılı ise, veya y=k.x olur.
y=k.x in grafiği aşağıdaki gibidir.
x, y ve z sayıları sırasıyla a, b ve c sayıları ile doğru orantılı ise olur.
Not: a ve b sıfırdan farklı reel sayılar olmak üzere, y= ax + b eşitliğini sağlayan x ve y değerleri doğru orantılı değildir. Ancak, x in değişme miktarı ile y nin değişme miktarı doğru orantılıdır.
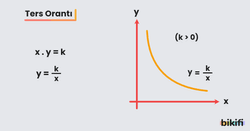
Ters Orantı
İki çokluktan biri artarken diğeri de aynı oranda azalıyorsa bu iki çokluk ters orantılıdır denir. Ters orantılı iki çokluğun çarpımı sabittir.
y ile x ters orantılı ise, y.x=k veya olur.
in grafiği aşağıdaki gibidir.
x, y ve z sayıları sırasıyla a, b ve c sayıları ile ters orantılı ise olur.
Not: x, y, z sayıları sırasıyla a, b, c sayılarıyla ters orantılı ise, sayılarıyla doğru orantılıdır. dir.
Bileşik Orantı
İki veya daha fazla oran bulunduran orantılara bileşik orantı denir. y sayısı; x ile doğru, z ile ters orantılı ise, olur.
Oran Orantı Problemleri
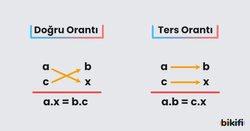
Problemlerde orantı kurulurken, aynı cinsten çokluklar alt alta gelecek şekilde yazılır. Doğru orantı için çapraz, ters orantı için paralel oklar çizilir. Daha sonra oklar yönünde çarpma işlemi yapılıp elde edilen iki çarpım eşitlenir.
İş problemlerinde ise kapasite, zaman, işçi sayısı vb gibi bütün değişkenler yapılan işle doğru orantılı olduğundan, yapılan işin değişkenlerin çarpımına oranı sabittir.
Yani iş problemlerinde doğru ve ters orantı birlikte sorulabilir, burada bileşik orantı verilmiş olur. Bu sorular yukarıda anlatılan şekilde çözülebilir.
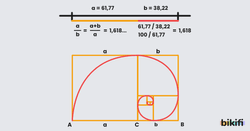
Altın Oran
Uzunluğu olan bir AB doğru parçası alalım ve bunu bir C noktası yardımıyla uzunlukları a ve b kadar olan AC ve BC doğrularına ayıralım. eşitliğini sağlayan oranının pozitif değerine altın oran adı verilir. Bu oran irrasyonel sayısına eşit olup yaklaşık değeri 1,618 dir.