Bir fonksiyonun tanım kümesinden 2 farklı eleman değer kümesinde aynı elemanla eşleşebilir ve aynı zamanda değer kümesinde eşleşmeyen elemanlar kalabilir. Bir fonksiyonun tersini düşündüğümüzde değer kümesinde birden fazla eşleşen eleman artık tanım kümesi olduğu için fonksiyonun kuralları gereği değer kümesinden birden fazla elemanla eşleşemez veya tan�ım kümesinde boşta eleman olamaz. Bunun direkt baştan halledilmesi açısından fonksiyonun tersi alınmadan önce bire bir ve örten fonksiyon olup olmadığını kontrol ederek tersinin alınabileceğini anlarız. Bir fonksiyon bire bir ve örten ise bu fonksiyonun tersi alınabilir. Anlattığımız bu durumu aşağıda görsellerle de açıklayalım.
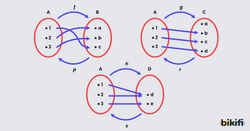
- f fonksiyonunu incelediğimizde bire bir ve örten olduğunu görürüz. f fonksiyonundaki bağıntılara tersten bakarsak B tanım kümesi, A değer kümesi olur. Tanım kümesindeki bütün elemanların karşılığı var ve birden fazla elemanla eşleşmemiş. Sonuç olarak p bağıntısı bir fonksiyondur ve f fonksiyonunun tersi vardır.
- g fonksiyonuna bakarsak bire bir veya örten değildir. g fonksiyonunu tersten incelediğimizde C kümesi tanım kümesi olacaktır fakat a elemanının bir karşılığı olmadığı için r bağıntısı bir fonksiyon değildir. Böylelikle g fonksiyonunun tersi yoktur.
- h fonksiyonu için örten diyebiliriz fakat bire bir değildir. h fonksiyonuna tersten baktığımızda D kümesi tanım kümesi olacaktır. D kümesindeki “d” elemanı değer kümesinde 2 elemanla eşleştiği için s bağıntısı bir fonksiyon değildir. Bu nedenle h fonksiyonunun tersi yoktur.
Bu örneklerden sonra anladığımız üzere bir fonksiyonun tersinin olabilmesi için bire bir veya örten olması şartlarından yalnızca biri değil iki şartın da sağlanması gerekmektedir.
Bir fonksiyonun ve tersinin gösterimi:
Fonksiyonun Tersini Almak
fonksiyonunun tersini almak için öncelikle fonksiyonun x bilinmeyenini yalnız bırakmalıyız. Daha sonra y ve x değerlerinin yerlerini değiştirdiğimizde yeni oluşan x bilinmeyenli bölüm ters fonksiyon olacaktır.
Örnek: fonksiyonunun tersini bulalım.
İlk olarak olduğundan eşitliğini yazarız. Bu denklemde x bilinmeyenini yalnız bırakalım.
Şimdi y ile x bilinmeyeninin yerlerini değiştiririz ve artık x içeren bölüm bizim ters fonksiyonumuzdur.
Fonksiyonun Tersini Almanın Kısayolları
Bir fonksiyonun tersini alırken yukarıdaki adımları takip ederiz fakat bazı kısayollar sayesinde bu işlemleri uzun uzun yapmaya gerek kalmaz. Bu kısayollar sayesinde soruları daha işlemsiz ve hızlı bir şekilde çözebilirsiniz.
İlk olarak gibi fonksiyonların tersini alırken x’in katsayısı(a) olan paydaya geçip yanında tam sayı(b) varsa işaret değiştirir.
Yukarıdakinin tersine gibi fonksiyonlarda bu sefer paydadaki sayı(a) x’in katsayısı olarak yukarı çıkar ve yine x’in yanında tam sayı(b) varsa işareti değiştir.
Şimdi yine kesirli fakat x’in bir katsayısı olacak şekilde yani gibi fonksiyonların tersini alırken x’in katsayısı(a) ile paydadaki tam sayı(c) yer değiştirir ve yine x’in yanındaki tam sayı(b) işaret değiştirir.
Bu aslında hemen yukarıda verdiğimiz kısayolla aynı mantık fakat orada x’in katsayısı 1 olduğu için paydadaki tam sayı yukarı çıkıyor gibi ama aslında 1 ile yer değiştiriyor. Zaten 1 sayısı paydaya geldiğinde görmezden geliyoruz.
Şimdi bir seviye ileri giderek hem pay hem de paydada x’li ifadelerin olduğu gibi fonksiyonların tersini almanın kısayolunu öğreneceğiz. Burada sadece yukarıdaki x’in katsayısıyla(a) aşağıdaki tam sayı(d) yer değişir ve her ikisi de işaret değiştirir.
Aşağıda kendisi ve tersi verilen fonksiyonları inceleyelim.
Ters Fonksiyonun Özellikleri
Özellik 1: Bir fonksiyonun tersi ile bileşkesi birim fonksiyonu verir.
Özellik 2: Bir bileşke fonksiyonunun tersini aldığımızda bileşke fonksiyon içindeki fonksiyonların tersi alınır ve yer değiştirirler.
Özellik 3: Bir fonksiyonun tersinin tersi kendisidir.
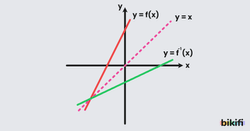
Özellik 4: Bir fonksiyonun grafiğinin y=x doğrusuna göre yansıması bu fonksiyonun tersinin grafiğini verir.
Ters fonksiyonun özellikleriyle ilgili örnekler çözelim.
Örnekler
Örnek1: olmak üzere fonksiyonunun tersi ile bileşkesini bulalım.
İlk olarak fonksiyonun tersini bulalım.
Fonksiyonun tersini bulduğumuza göre artık bileşkelerini bulabiliriz.
Bir fonksiyonu tersiyle bileşkesini aldığımızda birim fonksiyonunu elde ettik.
Örnek 2: İlk örnekte bir fonksiyonunun ilk aşamada tersini almıştık. Şimdi aynı fonksiyonun tersinin tekrar tersini alarak ne bulacağımıza bakalım.
Bir fonksiyonun tersini bulduktan sonra tekrar tersini almak aslında aynı işlemleri geriye sarmak gibidir. Bu nedenle tersinin tersini aldığımızda fonksiyonun yine kendisini buluruz.
Örnek 3: olmak �üzere fonksiyonları için bileşke fonksiyonunun tersini bulalım.
İlk olarak bileşkeyi çözerek tersini bulalım.
Şimdi ise direkt bileşke fonksiyonun tersini alarak bileşke fonksiyonu çözelim.
Görüldüğü üzere iki yoldan da aynı sonuca ulaştık. Yani bir bileşke fonksiyonun tersi istendiğinde istersek bileşke fonksiyonu çözüp en son tersini alabiliriz veya ilk baştan bileşke fonksiyonun içindeki fonksiyonların terslerini alıp yerlerini değiştirerek normal bileşke fonksiyon gibi çözebiliriz.
Örnek 4: olduğuna göre f(x) fonksiyonunu bulalım.
Verilen bileşke fonksiyonun sonuna bir de g(x) fonksiyonunun tersini eklersek bir fonksiyonun tersiyle bileşkesi birim fonksiyonu vereceğinden elimizde sadece f(x) fonksiyonu kalır. O zaman ilk iş olarak g(x) fonksiyonunun tersini alalım. Yukarıda öğrendiğimiz kısayollara göre g(x) fonksiyonunun tersini alırken yukarıdaki x’in katsayısı olan 2 ile aşağıda bulunan 1 tam sayısının yerlerini ve işaretlerini değiştiririz.
g(x) fonksiyonunun tersini bulduğumuza göre bileşke fonksiyonda x gördüğümüz yere g(x)�’in ters fonksiyonunu yazarak ekleyebiliriz.