Koordinat düzleminde bir birim çember açısı yapan bir doğruyla P noktasında keşissin. P noktasının x eksenindeki değeri K, y eksenindeki değeri L olsun.
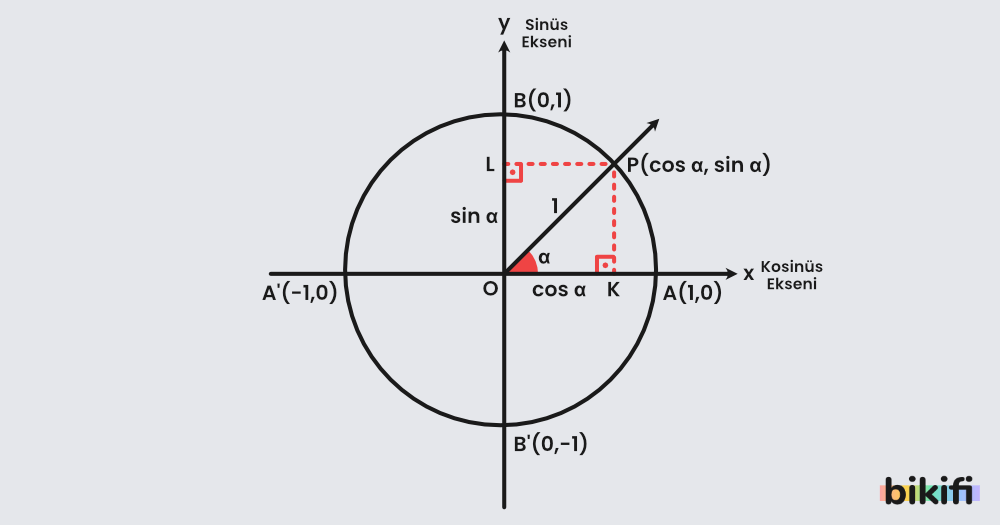
OKP dik üçgeninde açısının sinüs ve kosinüs değerlerini incelemek istersek;
- Sinüs değeri, karşı dik kenarın hipotenüse bölümünden elde edilir. Birim çemberde hipotenüs uzunluğumuz 1 olduğu için sinüs değerimiz karşı dik kenar uzunluğuna yani y eksenindeki değer olan L’ye eşit olur.
- Kosinüs değeri, komşu dik kenarın hipotenüse bölümünden elde edilir. Birim çemberde hipotenüs uzunluğumuz 1 olduğu için kosinüs değerimiz komşu dik kenar uzunluğuna yani x eksenindeki değer olan K’ye eşit olur.
Buradan çıkardığımız sonuç, birim çember üzerindeki bir noktanın x ekseninde gördüğümüz değeri cos, y ekseninde gördüğümüz değeri sin olarak ifade edilir.
Sinüs ve Kosinüs Fonksiyonları
Birim çember üzerinde sinüs ve kosinüsü incelediğimizde çemberin eksenleri kestiği değerlerin en büyük 1, en küçük ise -1 olduğunu görürüz. Sinüs ve kosinüs değerlerimiz de açılara göre x ve y eksenlerinde okunan 1 ile -1 arasındaki bir değere eşit olacaktır.
Bir dik üçgende iki dik kenarın kareleri toplamı hipotenüsün karesine eşit olduğu için, birim çemberde dik kenarlardan birisi sinüs diğer kenar ise kosinüs değeri olduğu ve hipotenüs birim çemberde 1 olduğu için sinüs ve kosinüsün kareleri toplamı 1’e eşit olacaktır.
Birbirini 90º ‘ye tamamlayan açılardan birinin sinüs değeri diğer açının kosinüs değerine eşit olacaktır. Bunun nedeni bir dik üçgen düşündüğümüzde dar açılardan birinin sinüs değerinde karşı dik kenarı hipotenüse bölerken diğer açının kosinüs değerini bulmak için komşu dik kenarı aldığımız zaman aslında aynı kenarı kullanmış oluruz.
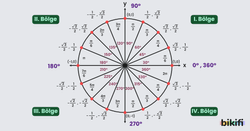
Yukarıdaki görselde belli açılarda kosinüs ve sinüs değerleri verilmiştir. Aşağıdaki başlıklarda ise sinüs ve kosinüs için farklı açılara göre değerleri ve kendi içindeki eşitliklerden yukarıdaki görsele de değinerek bahsedeceğiz.
Sinüs Fonksiyonu
Koordinat düzleminde birim çember 0º ‘den 180º ‘ye kadar olan açılarda y eksenini pozitif, 180º ‘den 360º ‘ye kadar olan açılarda ise negatif noktalarda kesmektedir. Birim çemberde y ekseninde gördüğümüz değer bize sinüsü verdiğine göre 0º-180º arasında sinüsün işareti pozitif(+) ,180º-360º arasında sinüsün işareti negatif(-) olacaktır.
Koordinat düzleminde bir açıyı 180º ‘den çıkartırsak bu açının y eksenine göre simetriğini almış oluruz. Bu durumda y eksenindeki değerinde bir değişiklik olmayacağından aşağıdaki sonuca varabiliriz.
Koordinat düzleminde bir açıyı 360º ‘den çıkartırsak veya açının negatifini alırsak bu açının x eksenine göre simetriğini almış oluruz. Bu durumda y eksenindeki değer zıt işaretli olacağından aşağıdaki sonuca varabiliriz.
Not: Bir açının 360º ‘den çıkarılmış hali bu açının negatifini almakla aynı şeydir. Çünkü negatifi alınmış bir açıya aynı açıyı elde edersiniz ve bu açıyı 360º ‘den çıkarmanızla eş değer olur.
Yukarıdaki birim çember görselinden bu iki durumu inceleyebilirsiniz.
Ayrıca aşağıdaki tablodan sinüsün derece ve radyan cinsinden bazı değerlerine ulaşabilirsiniz.
| 0 | 30 | 45 | 60 | 90 | 120 | 135 | 150 | 180 | 270 | 360 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| rad | 0 | ||||||||||
| 0 | 1/2 | 1 | 1/2 | 0 | -1 | 0 |
Kosinüs Fonksiyonu
Koordinat düzleminde birim çember 0º ‘den 90º ‘ye ve 270º ‘den 360º ‘ye kadar olan açı aralıklarında x ekseni pozitif, 90º ‘den 270º ‘ye kadar olan açılarda negatif noktalarda kesmektedir. Birim çemberde x ekseninde gördüğümüz değer bize kosinüsü verdiğine göre 0º-90º ve 270º-360º aralıklarında kosinüsün işareti pozitif(+), 90º-270º arasında kosinüsün işareti negatif(-) olacaktır.
Koordinat düzleminde bir açıyı 180º ‘den çıkartırsak bu açının y eksenine göre simetriğini almış olacağımızı söylemiştik. Bu durumda x eksenindeki değer zıt işaretli olacağından aşağıdaki sonuca varabiliriz.
Koordinat düzleminde bir açıyı 360º ‘den çıkartırsak veya açının negatifini alırsak bu açının x eksenine göre simetriğini almış olacağımızı söylemiştik. Bu durumda x eksenindeki değerinde bir değişiklik olmayacağından aşağıdaki sonuca varabiliriz.
Kosinüsteki bu durumları da yukarıdaki birim çemberden incelebilirsiniz.
Aşağıdaki grafikten derece ve radyan açı büyüklüklerine göre bazı kosinüs değerlerini görebilirsiniz.
| 0 | 30 | 45 | 60 | 90 | 120 | 135 | 150 | 180 | 270 | 360 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| rad | 0 | ||||||||||
| 0 | 1/2 | 0 | -1/2 | – | – | -1 | 0 | 1 |
Tanjant ve Kotanjant Fonksiyonları
Tanjant ve kotanjant fonksiyonları hakkında ayrı ayrı bilgi verip sonrasında trigonometrik fonksiyonların bölgelere göre işaretlerinden bahsedeğiz.
Tanjant Fonksiyonu
Bir dik üçgende bir dar açının tanjant değerini karşı dik kenarı komşu dik kenara bölerek bulabiliriz. Ayrıca bu açının sinüs değerini kosinüs değerine bölerek yine tanjant değerini bulabiliriz.
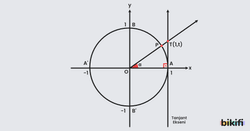
Birim çemberde tanjant değerini bulurken bir tanjant ekseninden faydalanabiliriz.
Tanjant ekseni (x=1 ve x=-1 doğruları) birim çemberi x ekseniyle kesiştiği noktalarda teğet geçer. Yukarıdaki görsele baktığımızda bir açısı yapan doğru tanjant ekseni olan x=1 doğrusunu T noktasında kesiyor. Oluşan OAT üçgeninine baktığımızda T noktası nereye denk gelirse gelsin açısına göre komşu dik kenarımızın uzunluğu her zaman 1 olacağı için karşı dik kenar olan T noktasının yüksekliği(y eksenindeki değeri) tanjant değerini verecektir.
Bir açısını 180º veya 360º ‘den çıkarmak bu açıyı x eksenine veya y eksenine göre simetriğini almak olduğu için bu açının tanjant değerini negatif yapar. Çünkü tanjant değeri sinüs ve kosinüs değerlerine bağlı olduğu için x eksenine göre simetri almak sinüsü, y eksenine göre simetri almak kosinüsü negatif yapacağı için tanjant değeri de negatif olacaktır.
Fakat açısına 180º eklediğimiz veya çıkardığımız zaman hem sinüs hem de kosinüsün işareti değiştiği için tanjantın işareti ve değeri aynı kalacaktır.
Şimdi ise sinüs ve kosinüs değerlerini sıfır yapan özel durumlara bakalım.
Sinüs 0º ve 180º ‘lerde sıfıra eşit olur ve tanjant değerini bulurken sinüsü kosinüse böldüğümüzde sinüs pay kısmını sıfır yaptığı için tanjant bu açılarda sıfıra eşit olur.
Kosinüs 90º ve 270º ‘lerde sıfıra eşit olur ve tanjantı değerini bulurken paydayı sıfır yaptığı için sonuç tanımsız olur. Bir başka bakış açısıyla bu açılarda giden bir doğru tanjant eksenine paralel gider ve hiç kesişmez. Biz tanjant doğrusunda bir değer göremediğimiz için sonuç tanımsızdır.
Kotanjant Fonksiyonu
Bir dik üçgende bir dar açının kotanjant değerini komşu dik kenarını karşı dik kenara bölerek bulabiliriz. Ayrıca bu açının kosinüs değerini sinüs değerine bölerek yine kotanjant değerini bulabiliriz.
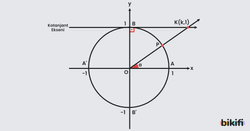
Birim çemberde kotanjant değerini bulurken aynı tanjanttaki gibi bir kotanjant ekseninden faydalanabiliriz.
Kotanjant ekseni (y=1 ve y=-1 doğruları) birim çemberin y ekseniyle kesiştiği noktalarda teğet geçer. Yukarıdaki görsele göre bir açısı yapan doğru kotanjant doğrusunu kestiği noktadaki x değeri bize açısının kotanjant değerini verir çünkü kotanjant ekseninin karşı kenarı her zaman 1’e eşit olacağından komşu kenar bizim kotanjantımıza eşit olacaktır.
Bir açısını 180º veya 360º ‘den çıkarmak aynı tanjant bölümünde anlattığımız gibi sinüs veya kosinüsten birini negatif yapacağından kotanjant değeri de negatif olacaktır.
Bu sefer açısına 180º eklediğimiz veya çıkardığımız zaman hem sinüs hem de kosinüsün işareti değiştiği için kotanjantın işareti ve değeri aynı kalacaktır.
Bu seferde kotanjant için sinüs ve kosinüs değerlerini sıfır yapan durumları inceleyelim.
Sinüs 0º ve 180º ‘lerde sıfıra eşit olur ve kotanjant değerini bulurken kosinüsü sinüse böldüğümüzde sinüs payda kısmını sıfır yaptığı için kotanjant bu açılarda tanımsız olur. Diğer bir deyişle bu açılar hiçbir zaman kotanjant eksenini kesmez.
Kosinüs 90º ve 270º ‘lerde sıfıra eşit olduğu için kotanjantın pay kısmını sıfır yapacaktır. Bu nedenle kotanjant bu açılarda sıfıra eşit olacaktır.
Sekant ve Kosekant Fonksiyonları
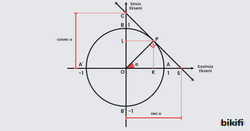
açısı yapan bir doğruyla birim çemberin kesiştiği nokta P olsun. P noktasından birim çembere teğet olan bir doğru x eksenini S, y eksenini C noktasında kesiyor olsun.
P noktasından teğet geçen doğrunun x eksenini kestiği S noktası bize açısının sekant değerini, y eksenini kestiği C noktası bize açısının kosekant değerini verir.
Aşağıda ayrı ayrı bu durumu inceleyelim.
Sekant Fonksiyonu
OPS üçgenine baktığımızda açısının kosinüs değeri olan komşu dik kenar bölü hipotenüsü hesaplarken komşu dik kenar her zaman 1 ve hipotenüs uzunluğumuz S olacağından 1/S gelecektir fakat biz bu değerin çarpmaya göre tersini yani üzeri -1 ‘ini alırsak sekant değerimizi elde ederiz.
Bu durumda cos ‘yı sıfır yapan 90º ve 270º açıları sekant fonksiyonunu tanımsız yapacaktır. Birim çemberde incelediğimizde bu açılara geldiğinde P noktasından geçen teğet doğru x(kosinüs) eksenine paralel olacak ve kesişemeyecektir. Böylelikle bir S değeri oluşmayacak ve tanımsız olacaktır.
Kosekant Fonksiyonu
OPC üçgenine baktığımızda OCP açısı olan açısının sinüs değeri olan karşı dik kenar bölü hipotenüsü hesaplarken karşı dik kenar her zaman 1 ve hipotenüs uzunluğumuz C olacağından 1/C gelecektir fakat çarpmaya göre tersini aldığımız zaman bize kosekant değerini verecektir.
Şimdi de kosekant fonksiyonunu tanımsız yapan açılara bakarsak sinüs fonsiyonunu sıfır yapan 0º ve 180º açıları kosekantı tanımsız yapar. Birim çemberde incelediğimizde bu açılara geldiğinde P noktasından geçen teğet doğru y(sinüs) eksenine paralel olacak ve kesişemeyecektir. Böylelikle bir C değeri oluşmayacak ve tanımsız olacaktır.
Trigonometrik Fonksiyonların Bölgelere göre İşaretleri
Belli bir açı yapan doğruyla birim çemberin kesiştiği noktanın x eksenindeki değeri açının kosinüs değerine, y eksenindeki değeri de sinüs değerine eşit olduğunu söylemiştik. Şimdi buradan yola çıkarak bölgelere göre trigonometrik fonksiyonların işaretlerini inceleyelim.
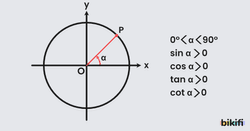
1. Bölge
0º-90º arasında x ve y eksenlerindeki değerler sıfırdan büyük olduğu için sinüs ve kosinüs değerleri pozitiftir. Sinüs ve kosinüs değerlerinin aynı işaretli olması tanjant ve kotanjant değerlerini de pozitif yapacaktır.
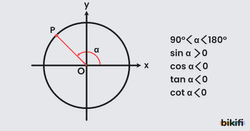
2. Bölge
90º-180º arasında y eksenindeki değer sıfırdan büyük olduğu için sinüs pozitif, x eksenindeki değer sıfırdan küçük olduğu için kosinüs değeri negatif olacaktır. Sinüs ve kosinüs değerlerinin zıt işaretli olması tanjant ve kotanjant değerlerini negatif yapacaktır.
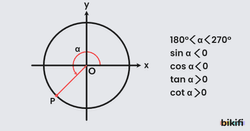
3. Bölge
180º-270º arasında x ve y eksenlerindeki değerler sıfırdan küçük olduğu için sinüs ve kosinüs değerleri negatiftir. Sinüs ve kosinüs değerlerinin aynı işaretli olması tanjant ve kotanjant değerlerini de pozitif yapacaktır.
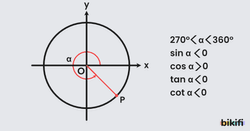
4. Bölge
270º-360º arasında x eksenindeki değer sıfırdan büyük olduğu için kosinüs pozitif, y eksenindeki değer sıfırdan küçük olduğu için sinüs değeri negatif olacaktır. Sinüs ve kosinüs değerlerinin zıt işaretli olması tanjant ve kotanjant değerlerini negatif yapacaktır.