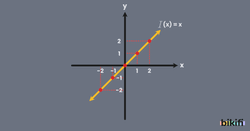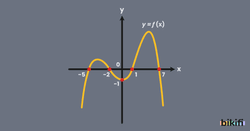Grafik Çizimi
Koordinat düzleminde yatay eksen tanım kümesini, düşey eksen ise değer kümesini temsil eder. Örnek olarak tanım kümesinden seçtiğimiz bir x sayısını yatay eksende buluruz, fonksiyonun değer kümesinde bu x sayısına karşılık gelen değeri düşey eksende bularak bu iki eksendeki sayıların kesişim noktasını alırız. Bu işlem fonksiyonun tanım kümesindeki tüm sayılar için yapıldığında karşımıza fonksiyonun grafiği çıkar.
Basit bir örnekle başlarsak olmak üzere fonksiyonunun grafiğini çizelim.
Bu fonksiyonda x yerine koyacağımız değerler bize direkt y değerini verecektir yani eşit olacaklar.
Yukarıda bulduğumuz (-2,-2), (-1,-1), (0,0), (1,1), (2,2) noktalarını koordinat düzleminde yerine koyup birleştirdiğimizde fonksiyonunun doğrusal grafiğini elde edeceğiz.
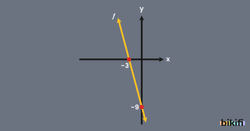
Başka bir örnek ise olmak üzere fonksiyonun grafiğini çizelim.
Bu fonksiyonlar için yöntemimiz iki ekseni de sıfır yapan durumlar bulunarak eksenlerin kaçta kesildiğini buluruz. Fonksiyonda x bilinmeyeninin üssü 1 olduğu için doğrusal bir grafik olacaktır. Bu nedenle bulduğumuz bu noktaları birleştirdiğimizde fonksiyonunun grafiğini elde etmiş oluruz.
Bulduğumuz (0,-9) ve (-3,0) noktalarını işaretleyip birleştirdiğimizde aşağıdaki gibi bir grafik elde ederiz.
Bu sefer biraz daha karışık bir örnek çözelim.
olmak üzere
fonksiyonunun grafiğini çizelim.
Öncelikle üç parçadan oluşan fonksiyonumuzun her bölümünü ayrı inceleyeceğiz.
İlk olarak x değerinin sıfırdan küçük olduğu durumu incelediğimizde x yerine yazılan sayıların çarpmaya göre tersi bize y değerini verecektir. Bu durumlarda negatif işareti bir kenara koyduğumuzda x sayı değeri olarak büyüdükçe y küçülecek, x küçüldükçe y büyüyecektir. Aşağıda bu durumu açıklayacak birkaç örnek değer bulacağız ve en son grafikte göstereceğiz. Burada fonksiyona ait bütün noktaları bulamasak bile grafiğin nasıl ilerleyeceğini tahmin ederek devamı çizilir.
ise
aralığındaki noktaların bazıları: ,,,,,
Bir sonraki bölüme geçince x değerinin karesi alındığı için küçük değerlerde x ve y değerleri birbirine yakın olacaktır fakat x değeri büyüdükçe y çok daha fazla büyümeye başlayacaktır.
ise
[0, 2) aralığındaki noktaların bazıları: ,,,,,
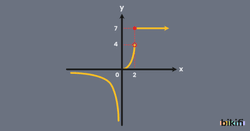
Son bölüme geldiğimizde x değerinin 2 ve daha büyük olduğu her sayı için yani [ aralığında sonuç her zaman 7 olacaktır. Fonksiyonun her parçası için bulduğumuz bu noktaları koordinat düzleminde birleştirdiğimizde ortaya aşağıdaki gibi bir grafik çıkacaktır.
Fonksiyon Grafiklerini Yorumlama
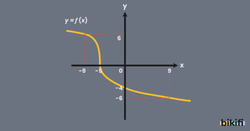
Fonksiyonların grafiğini incelediğimizde ilk olarak fonksiyonun x ve y eksenlerindeki aralıklarına bakarak tanım ve değer kümesi hakkında yorum yapabiliriz. Bir fonksiyonun grafiğinin x eksenindeki en büyük ve en küçük değeri tanım kümesinin aralığını bize verir. Benzer şekilde grafiğin y eksenindeki aralığı bize değer kümesinin aralığını verecektir.
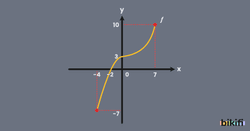
Örnek olarak aşağıdaki grafiğe baktığımızda x eksenini en küçük -4 değerinden başlarken en büyük 7 değerinde bitiyor. Buna göre tanım kümemiz [-4,7] aralığı olacaktır. Diğer yandan y eksenindeki aralığını bulmak istediğimizde y ekseninde aldığı en küçük değer -7, en büyük değer 10 olur. Buradan değer kümesinin [-7,10] aralığında olduğunu bulmuş olduk.
Fonksiyonlar her zaman yukarıdaki gibi bir noktada bitmeyebilir. Grafikte sonunu görmediğimiz sürekli ilerleyen fonksiyonların tanım kümeleri reel sayılar olur. Fonksiyonun grafiğini inceleyip y ekseninde belli bir aralıkta mı yoksa sonunu görmediğimiz şekilde mi ilerliyor gözlemleyebilir ve ona göre değer kümesini yazabiliriz.
Fonksiyonun Ters Görüntüsü
Bir fonksiyonda x değerinin görüntüsü y’dir. Fonksiyonun ters görüntüsü alındığında ise tanım ve görüntü kümeleri yer değiştirerek artık y değerinin görüntüsü x şeklinde olur.
Örnek olarak tanım kümesi [-2,6] ve görüntü kümesi [-7,8] aralığı olan bir fonksiyonun ters görüntüsünü almak istediğimizde artık tanım kümesi [-7,8] ve görüntü kümesi [-2,6] aralığı olur. Ters görüntüyü direkt grafiğini gördüğümüz bir fonksiyonda uygulayalım.
Örnek: Aşağıdaki grafiğe sahip fonksiyonun [-6,6] aralığındaki ters görüntüsünü bulalım.
Öncelikle [-6,6] aralığının ters görüntüsü isteniyorsa ilk durumda bu aralık görüntü kümesine ait olacaktır. Bu durumda y eksenindeki bu aralığın x eksenindeki karşılığını bulursak tanım kümesinin aralığını buluruz. Bulduğumuz bu aralık fonksiyonun istediğimiz aralıktaki ters görüntüsü olacaktır.
Fonksiyonun [-6,6] aralığındaki ters görüntüsü [-9,9] aralığı olacaktır.
Ters görüntüyle ilgili son bir örnek daha çözelim.
fonksiyonunun [-25,66] aralığındaki ters görüntüsünü bulalım.
Bir önceki örnekte de olduğu gibi ters görüntü için verilen aralık aslında normal fonksiyonda y değerleridir, ters görüntüsü de aslında fonksiyonun tanım kümesi yani x değerleridir. Ters görüntüsünü almamız istenilen fonksiyonun aralığı fonksiyonda y değeri yerine yazarak x aralığını buluruz. Bu da bize ters görüntüyü verir.
Fonksiyonun [-25,66] aralığındaki ters görüntüsü [-3,4] olacaktır.
Düşey Doğru Testi
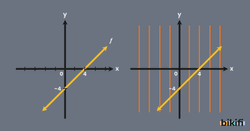
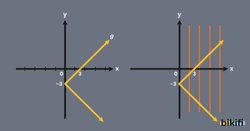
Fonksiyonun tanımını yaparken tanım kümesindeki her eleman değer kümesinden sadece bir karşılığı olabileceğini söylemiştik. Fonksiyonun bu kurala uygun olup olmadığını grafikte tanım kümesi boyunca düşey çizgiler çekerek öğrenebiliriz. Çizilen bu çizgiler grafiği birden fazla noktada kesiyorsa tanım kümesindeki elemanın birden fazla değere karşılık geldiği görülür. Bu durumda bu bağıntı fonksiyon olmayacaktır. Grafiği verilen bağıntının fonksiyon olup olmadığını öğrenebildiğimiz bu yönteme düşey(dikey) doğru testi denir.
Yukarıda verilen görsellerde iki farklı bağıntıya düşey doğru testi uygulanmıştır. İlk görselde düşey çizgiler grafiği hep bir noktada kesmiştir, bu yüzden bu bağıntı fonksiyondur. Fakat alttaki grafiğe geldiğimizde düşey çizgiler sürekli grafiği iki noktada kesmektedir. Düşey çizgilerin sadece birinin dahi grafiği iki noktada kesmesi bu bağıntının fonksiyon olmadığını belirtir.
Denklemin Köklerini Bulma
Grafiği verilen bir fonksiyonun x eksenini kestiği noktalar bize denklemin köklerini verir.
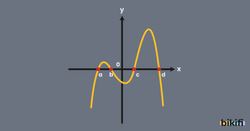
Yukarıdaki grafikte
denkleminin kökleri grafiğin x eksenini kestiği değerler olan a, b, c ve d değerleridir.
eşitsizliğinin çözüm kümesi x ekseninin üstünde kalan aralıklar olacaktır.
eşitsizliğinin çözüm kümesi bu sefer x ekseninin altında kalan tüm aralıkların birleşimidir.
Örnek: Grafiği verilen fonksiyonunda eşitsizliğini sağlayan x tam sayı değerlerinin toplamını bulalım.
Grafikte x ekseni üstünde kalan bölüm eşitsizliğini sağlar. Bu aralığın tamamı birleşimidir. Burada bulunan tam sayıların toplamı
-5-4-3-2+1+2+3+4+5+6+7=14 olur.