Fonksiyonların Bire Birliğinin ve Örtenliğinin İncelenmesi
Fonksiyonun Bire Bir ve Örten Olması
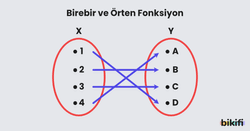
Boş küme olmayan A ile B kümeleri için f fonksiyonu, birebir fonksiyon ise her bir elemanın diğer kümenin bir elemanıyla eşleştiği fonksiyondur.
Örten fonksiyon ise görüntü kümesinde boşta eleman kalmayacak şekilde eşleşmenin gerçekleştiği fonksiyonlara denir.
Yatay Doğru Testi
Grafiği verilen bir fonksiyonun bire bir veya örten olup olmadığını x eksenine paralel yatay doğrular çizerek test edebiliriz. Bu yatay çizgilerin grafiği kesip kesmediği veya kaç noktada kestiği çok önemlidir. Çizilen bu yatay doğrular değer kümesindeki elemanlara tanım kümesinde bir karşılık olup olmadığını gösterir.
Eğer değer kümesindeki her eleman için çizilen yatay doğru grafiği en az bir noktada kesiyorsa bu fonksiyon örtendir, yalnızca bir noktada kesiyorsa bu fonksiyon bire birdir. Bir fonksiyon grafiğinde x eksenine paralel doğrular çizilerek yapılan bu teste ise yatay doğru testi denir.
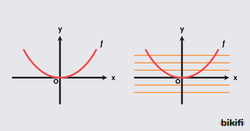
Bu görseli incelediğimizde f fonksiyonunun grafiğinde x ekseninin altında kalan yatay doğrulara baktığımızda grafiği herhangi bir noktada kesmediğini görürüz. Bu nedenle f fonksiyonu örten değildir. Ayrıca x ekseninin yukarısında kalan yatay doğrulara bakarsak grafiği ikişer noktada kestiklerini görürüz. Buradan f fonksiyonunun bire bir olmadığını da söyleyebiliriz.
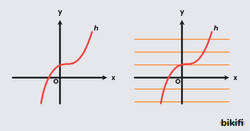
Bu görselde ise h fonksiyonunun grafiğinde ise yatay doğrular çizildiğinde her doğrunun grafiği bir noktada kestiğini görürüz. Buradan h fonksiyonunun bire bir ve örten fonksiyon olduğunu söyleyebiliriz.
Bileşke Fonksiyon
Örten bir fonksiyonun görüntü kümesinin başka bir fonksiyonun tanım kümesi olacak şekilde iki fonksiyonun tek bir fonksiyon haline gelerek oluşturduğu yeni fonksiyona bileşke fonksiyon denir.
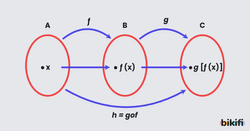
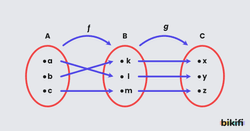
Bir örnekle açıklarsak A kümesinden B kümesine tanımlı f fonksiyonu ve B kümesinden C kümesine tanımlı g fonksiyonu olsun. Biz direkt A kümesinden C kümesine tanımlı fonksiyon oluşturmak istediğimizde f ve g fonksiyonun bileşkesinden faydalanırız.
Bileşke fonksiyon şeklinde yazılır ve “g bileşke f” diye okunur.
Bileşke fonksiyonlarda işlemler sağdan sola doğru yapılır. Bileşke fonksiyon iki veya daha fazla fonksiyondan oluşabilir. Her fonksiyon bir solundakinin içine yazılarak işlemler yapılabilir.
Aşağıda f ve g fonksiyonlarından oluşan bileşke fonksiyonu görsel olarak görebileceğimiz örneği inceleyelim.
Bileşke Fonksiyonun Özellikleri
Özellik 1: Fonksiyonlarda bileşke işleminin değişme özelliği yoktur. Yani fonksiyonların yerlerini değiştiremeyiz. Sağdaki fonksiyonu soldakinin içine yazdığımız için bir yer değiştirme durumunda tam tersi şekilde birini diğerinin içine yazmak tamamen farklı bir sonuç getirecektir karşımıza.
Özellik 2: Bir fonksiyonun birim fonksiyon () ile bileşkesi kendisine eşittir. Birim fonksiyona ne verirsek aynısını aldığımız için sağ veya sol tarafta olması önemsizdir.
Özellik 3: Fonksiyonlarda bileşke işleminin birleşme özelliği vardır. Yani bileşke işlemlerini aralarındaki sıra bozulmadığı sürece istenilen yerden başlayarak yapabiliriz.
Bileşke fonksiyonun bu 3 özelliğiyle ilgili birer örnek çözerek pekiştirelim.
Örnekler
Örnek 1: olmak üzere fonksiyonları için bileşke fonksiyonlarını bulalım.
Bulduğumuz bu sonuçlara göre bileşke işlemlerinde değişme özelliğinin olmadığını görürüz.
Örnek 2: olmak üzere fonksiyonları için bileşke fonksiyonlarını bulalım.
İşlemlerin sonucunda bileşke fonksiyonda birim fonksiyonun yeri değiştiğinde sonucun değişmediğini ve diğer fonksiyona eşit olduğunu görüyoruz.
Örnek 3: olmak üzere fonksiyonları için bileşke fonksiyonlarını bulalım.
Bileşke fonksiyonu iki farklı şekilde de çözdüğümüzde sonucun değişmediğini görüyoruz.