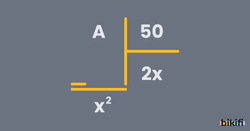Bölme işlemi çarpma işleminin tersi olan aritmetik işlemdir. Bir bütünün istenilen sayı kadar eş parçaya ayrılması temeline dayanır.
Tam Sayılarda Bölme Algoritması
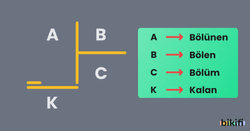
A, B, C, K tam sayılar ve olsun.
A: Bölünen
B: Bölen
C: Bölüm
K: Kalan
Yukarıdaki bölme işlemine göre,
- A=B.C + K
- K<B
- K=0 ise A sayısı B sayısına tam bölünür. Bu durum B|A şeklinde gösterilir.
Örnek: A sayısının B doğal sayısına bölümünden elde edilen bölüm 3 kalan 2 dir. Buna göre A sayısının alabileceği en küçük pozitif tam sayı değerini hesaplayalım.
Çözüm: A = 3B+2 dir. Kalan< bölen olduğundan 3<B olup B en az 4 olur. Buradan A’nın en küçük değeri, A=3B+2 3.4+2=14 olur.
Örnek: A ve x birer doğal sayı ve
olduğuna göre, A nın alabileceği en büyük değeri bulalım.
Çözüm: A=50.2.x + x2 şeklinde yazılabilir. A’nın en büyük olabilmesi için x in en büyük olması gerekir. x2 < 50 olduğuna göre, x en büyük 7 değerini alabilir. 7 değeri yerine yazılır ise A=50 .2 .7 + 72 = 749 olur.
A, B, x, m, n, c pozitif tamsayılar olmak üzere, A’nın x’e bölümünden kalan m, B’nin x’e bölümünden kalan n olsun.
- A.B nin x’e bölümünden kalan m.n dir.
- A B nin x’e bölümünden kalan m n dir.
- c.A’nın x’e bölümünden kalan c.m dir.
- Ac nin x’e bölümünden kalan mc dir.
Burada; m.n, mn, c.m ve mc sayıları x’ten küçük değilse bu değerler x’e tekrar bölünerek kalan belirlenir.
Asal Sayılar
Sadece kendisine ve 1 sayısına kalansız bölünebilen 1’den büyük tam sayılara asal sayı denir.
Aralarında Asal Sayılar
İki sayının 1 sayısından başka pozitif ortak böleni yoksa bu sayılara aralarında asal denir. Örneğin; 2 ile 3, 3 ile 4, 8 ile 15 sayıları aralarında asaldır.
Tam Sayılarda Bölünebilme Kuralları
Bu başlığın altında 2, 3, 4, 5, 6, 8, 9, 10 ve 11 ile bölünebilme kuralları incelenmiştir.
2 ile Bölünebilme
Çift sayılar 2 ile tam bölünür. Çift sayıların 2 ile bölümünden kalan sıfır, tek sayıların 2 ile bölümünden kalan ise 1’dir. Birler basamağında çift rakam {0, 2, 4, 6, 8} olan doğal sayılar 2 ile tam bölünür.
Bu kuralın nedenini inceleyelim. abc çok basamaklı bir doğal sayı ise 100a+10b+c şeklinde yazılabilir. 10 ve 10’un kuvvetleri 2’nin katı olduğundan 10b ve solunda bulunan terimler 2’ye tam bölünür. Bu yüzden sadece c’ye bakmak yeterli olur.
3 ile Bölünebilme
Bir doğal sayının rakamları toplamının 3 ile bölümünden kalan bu sayının 3 ile bölümünden kalana eşittir. 5672 sayısının 3 ile bölümünden kalan 5+6+7+2=20 elde edilir ve 20/3 işleminden kalan 2 olur. 5672 sayısının 3’e bölümünden kalan 2 olur.
Bu kuralın nedenini inceleyelim. abc çok basamaklı bir doğal sayı ise 100a+10b+c şeklinde yazılabilir. 10 ve 10’un kuvvetlerinin 3 ile bölümünden kalan 1 olduğu için sayıların yerine 1 yazılabilir. Bu durumda 100a+10b+c sayısında 10 ve kuvvetlerinin yerine 3 ile bölümünden kalanlar yazılır. 1a+1b+c şeklini alır ve rakamlar toplamı elde edilir.
4 ile Bölünebilme
Son iki (birler ve onlar) basamağı (iki basamaklı sayı gibi düşünülerek) 4’ün katı olan sayılar 4 ile tam bölünür, kalan için ise bu sayı 4 ile bölünerek bulunur.
1234 sayısının 4’e bölümünden kalanı hesaplayalım. 1234 sayısının son iki basamağı 34 olur ve 34 sayısının 4’e bölümünden kalan 1234 sayısının 4’e bölümünden kalana eşittir. 34=4.8+2 olduğundan 34 sayısının 4’e bölümünden kalan 2’dir.
5 ile Bölünebilme
Birler basamağı 0 veya 5 olan sayılar 5’e tam bölünür. Bir sayının 5’e bölümünden kalan, bu sayının birler basamağındaki rakamın 5’e bölümünden kalandır.
Bu kuralın nedenini inceleyelim. abc çok basamaklı bir doğal sayı ise 100a+10b+c şeklinde yazılabilir. 10 ve 10’un kuvvetleri 5’nin katı olduğundan 10b ve solunda bulunan terimler 5 ile tam bölünür. Bu yüzden sadece c’ye bakmak yeterli olur.
6 ile Bölünebilme
Hem 2 ile hem de 3 ile tam bölünebilen sayılar (3 ile tam bölünebilen çift sayılar) 6 ile tam bölünür.
8 ile Bölünebilme
Bir doğal sayının son üç basamağındaki rakamların oluşturduğu sayı, 8 in katı ise sayı 8 ile tam bölünür. Sayının 8 ile bölümünden kalan da aynı şekilde son üç basamağındaki sayının 8 ile bölümünden kalana eşittir.
6794120 sayısının 8 ile bölümünden kalan 0 dır. Sayı 8 e tam bölünür.
9 ile bölünebilme
Rakamlarının sayı değerlerinin toplamı 9 un katı olan sayılar 9 ile tam bölünür veya 9 ile bölümünden kalan da aynı şekilde rakamları toplamının 9 ile bölümünden kalana eşittir.
x ve y farklı iki sayı olmak üzere x5y4 dört basamaklı sayısı 9 ile tam bölündüğüne göre x + y değerini hesaplayalım.
x+5+y+4 değeri 9 a tam bölünüyor ise x + y 9 veya 18 olabilir fakat x ve y farklı olduğu için x+y=9 olur.
10 ile bölünebilme
Birler basamağı sıfır (0) olan sayılar 10 ile tam bölünür. Bir sayının birler basamağındaki sayı o sayının 10 ile bölümünden kalandır.
11 ile Bölünebilme
abcdef altı basamaklı bir sayı olsun. Sayının birler basamağından başlayarak sırasıyla rakamların önüne + ve – işaret yazılır ve rakamlar toplanır( -a +b -c +d -e +f). Oluşan bu toplam 11’in katı ise sayı 11’e tam bölünür. Bu toplam 11’e tam bölünmüyor ise kalan değer, sayının 11 ile bölümünden kalana eşittir.
Diğer Sayılara Bölünebilme
Aralarında asal iki sayıdan her birine bölünebilen bir sayı, bu sayıların çarpımına da bölünür.
Bir sayı aralarında asal olan a ve b sayısı gibi iki sayıya tam bölünüyor ise o sayı a.b değerine de tam bölünür.
2 ve 3’e tam bölünen bir sayı 6 ile tam bölünür. Bu yöntem ile birçok sayıya bölünebilme kuralı elde edilebilir.
- 12 ile bölünebilme kuralı; 3 ve 4’e tam bölünmeli
- 15 ile bölünebilme kuralı; 3 ve 5’e tam bölünmeli
- 18 ile bölünebilme kuralı; 2 ve 9’a tam bölünmeli
- 24 ile bölünebilme kuralı; 3 ve 8’e tam bölünmeli
- 30 ile bölünebilme kuralı; 3 ve 10’a tam bölünmeli
- 36 ile bölünebilme kuralı; 4 ve 9’a tam bölünmeli
şeklinde bulunur ve liste daha da uzatılabilir.
Tam Sayının Asal Çarpanları ve Tam Sayı Bölenleri
1’den büyük bütün sayılar asal çarpanlarının çarpımı şeklinde ayrılabilir. Bu, cebrin temel teoremlerinden biridir ve asal çarpanlara ayırma olarak adlandırılır.
120 sayısını asal çarpanlarına ayıralım.
| 120 | 2 |
| 60 | 2 |
| 30 | 2 |
| 15 | 3 |
| 5 | 5 |
| 1 |
2, 3, 5 sayıları 120’nin asal çarpanlarıdır.
Örnek: 800 sayısının asal sayı çarpanların�ın toplamını bulalım.
Çözüm: 800 = 25 . 52 şeklinde yazılabilir. 800’ün 2 tane asal sayı böleni vardır. Bunlar 2 ve 5’dir. Asal sayı çarpanlarının toplamı 2+5=7 şeklinde hesaplanır.
Tam Bölen Kavramları
A sayısının asal çarpanlarına ayrılmış şekli, A = xa . yb . zc olsun. (x, y ve z asal sayılar. a, b ve c doğal sayılar.)
- A’nın (a+1).(b+1).(c+1) tane pozitif tam böleni vardır.
- A’nın pozitif bölenlerinin sayısı kadar negatif bölenleri olduğundan, 2.(a+1).(b+1).(c+1) tane tam böleni vardır.
- A’nın asal sayı bölenleri a, b, c olmak üzere 3 tanedir.
- A’nın tamsayı bölenleri toplamı 0’dır.
- A’nın asal sayı bölenleri hariç tamsayı bölenlerinin toplamı -(x+y+z) dir.
Örnek
600 sayısının pozitif bölenlerinin kaç tanesi,
- tektir?
- çiftir?
- 3’ün katıdır?
- 12’nin katıdır?
Çözüm
Öncelikle 600’ü asal çarpanlarına ayıralım.
| 600 | 2 |
| 300 | 2 |
| 150 | 2 |
| 75 | 3 |
| 25 | 5 |
| 5 | 5 |
| 1 |
- Tek olanı bulmak için, öncelikle çift olan asal çarpanları yok saymamız gerekiyor.
- Yani, . 31 . 52 asal çarpanları kalıyor.
- Tam bölen başlığındaki 1. kuraldan dolayı
- (1+1)*(2+1) = 2 * 3 = 6 tane pozitif böleni tek sayıdır.
- Çift olanı bulmak için,
- Çiftliğin sağlanması için bir tane 2 böleni kullanılmalıdır.
- Yani, 2 ( 22 . 31 . 52 ) olarak değerlendirilir.
- Parantez içine yine yukarıdaki kuralı uygularsak,
- (2+1)*(1+1)*(2+1) = 3 * 2 * 3 = 18 tane pozitif çift sayı böleni vardır.
- 3’ün katı olan bölenleri bulmak için,
- 3’e bölünebilmesi için bir tane 3 bölenini dışarıda tutmalıyız.
- Yani, 3 (23 . 52) olarak değerlendirilir.
- Parantez içine yukarıdaki kuralı uygularsak,
- (3+1) * (2+1) = 4 * 3 = 12
- 12’nin katı olan bölenleri bulmak için,
- 12’ye bölünebilmesi için 12’nin asal çarpanlarını (2 tane 2, 1 tane 3) dışarıda tutmalıyız.
- Yani, 12 ( 21 . 52) olarak değerlendirilir.
- Parantez içine yukarıdaki kuralı uygularsak,
- (1+1) * (2+1) = 2*3 = 6
Tam Sayı Bölenlerinin Toplamını Bulmak
A = xa . yb . zc olsun. A sayısının pozitif bölenleri toplamı şu şekilde hesaplanır:
Örnek: 150 sayısının 3’ün katı olan pozitif tam bölenleri toplamı kaçtır?
Çözüm:
- 150 sayısı 2 * 3 * 52 şeklinde yazılır.
- 3’ün katı olan pozitif tam bölenlerin toplamı istendiği için 3 (2 * 52) şeklinde ifade edilir.
- Toplam yukarıdaki formülden:
- (21+ 20) * (52+51+50) = 3 * 31 = 93
- Hesaplamanın dışında kalan 3 bütün toplama etki edeceği için elde edilen 93 sayısını dışarıda tutulan 3 sayısıyla çarpmalıyız.
- 93 * 3 = 279 bize 150 sayısının 3’ün katı olan pozitif tam bölenleri toplamını verecektir.