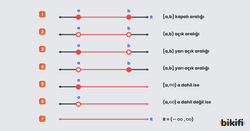
Kapalı Aralık
a ve b birer gerçek sayı olmak üzere, a<b olsun. a ve b sayıları ile bu sayılar arasında kalan tüm gerçek sayılar a, b kapalı aralığını oluştururlar ve bu aralık [a, b] şeklinde gösterilir.
- [a, b]={x | a ≤ x ≤ b, x R} (Yukarıdaki resimde 1 numaralı grafik)
Açık Aralık
a, b kapalı aralığından a ve b sayıları çıkarılırsa a, b açık aralığı elde edilir ve a, b açık aralığı (a, b) şeklinde gösterilir.
- (a, b)= {x | a < x < b, x R} (Yukarıdaki resimde 2 numaralı grafik)
Yarı Açık (Yarı Kapalı) Aralık
a, b kapalı aralığından a ve b sayılarından sadece birisi çıkarılırsa yarı açık aralıklar elde edilir. Buna göre, a, b kapalı aralığından a sayısı çıkartılırsa (a,b], b sayısı çıkartılırsa [a,b) yarı açık aralığı oluşur.
- [a, b) = {x | a ≤ x < b, x R} (Yukarıdaki resimde 3 numaralı grafik)
- (a, b] = {x | a < x ≤ b, x R} (Yukarıdaki resimde 4 numaralı grafik)
Üstten Sınırsız Aralıklar
a R olmak üzere a dan büyük tüm gerçek sayıların kümesidir
- [a, ) = {x | a ≤ x, x R} (Yukarıdaki resimde 5 numaralı grafik)
- (a, ) = {x | a < x, x R} (Yukarıdaki resimde 6 numaralı grafik)
Alttan Sınırsız Aralıklar
a R olamk üzere a dan küçük tüm gerçek sayıların kümesidir.
- (, a] = {x | x ≤ a, x R}
- (, a) = {x | x < a, x R}
R aralığı
R nin kendisi de aralıktır. R=() = {x | R }
- R = (, ) = {x | < x < , x R} (Yukarıdaki resimde 7 numaralı grafik)