Birinci dereceden iki bilinmeyenli denklem ve eşitsizlikleri önceki yazılarda tanımlamıştık. Bu yazıda ise denklem sistemlerini, çözüm yöntemlerini ve grafik çizimini ele alacağız.
Birinci Dereceden İki Bilinmeyenli Denklem Sistemleri
x ve y bilinmeyen, a ve b reel sayı, a1, a2, b1 ve b2 sıfırdan farklı olmak üzere
denklemlerinden oluşan sisteme birinci dereceden iki bilinmeyenli denklem sistemi denir. Bu denklemleri sağlayan x ve y gerçek sayılar ise (x, y) sıralı ikilisi olarak yazılır ve bu sıralı ikiliye denklemin çözüm kümesi denir. ax+by+c=0 birinci dereceden iki bilinmeyenli denklemlerinin grafikleri analitik düzlemde doğru belirtir. Bu denklemleri çözmek için yok etme, yerine koyma ve grafik çizimi gibi yöntemler kullanılır
Yok Etme Yöntemi
Denklem sisteminde aynı bilinmeyenlere sahip terimlerin katsayıları eşit ve ters işaretli olacak şekilde düzenlenir. Daha sonra taraf tarafa toplama yapılarak sadeleşmesi sağlanır.
Örnek olarak aşağıdaki denklem sisteminin çözüm kümesini bulalım.
denklemlerinde x bilinmeyenini yok etmek için ilk denklem 4 ikinci denklem -3 ile çarpılır.
Denklemler taraf tarafa toplanır ise 7y=-7 ⟹ y=-1 olur. y değeri herhangi bir denklemde yerine yazılır ise x değeri de bulunmuş olur. y=-1 ⟹ 3.x+4.(-1)=11 denkleminden x=5 bulunur.
Yerine Koyma Yöntemi
Denklem sistemindeki bilinmeyenlerden herhangi biri yalnız bırakılır ve diğer denklemde yerine yazılır. Bu yöntem ile çözüm kümesi elde edilebilir.
Örnek olarak
denklem sisteminin çözüm kümesini yerine koyma yöntemiyle bulalım.
x+5y=-5 denkleminde x yalnız bırakılır ise x=-5y-5 olur. İkinci denklemde x yerine -5y-5 yazılır ise 3(-5y-5)-2y=19 olur. y=-2 bulunur ve x değerini bulmak için herhangi bir denklemde y yerine -2 yazılır ise x=5 bulunur.
Grafik Yorumu
Birinci dereceden iki bilinmeyenli bir denklemin çözüm kümesinin oluşturduğu sıralı ikililer analitik düzlemde bir doğru belirtir. Denklem sisteminin oluşturduğu doğruların kesişim noktası veya noktaları bu denklem sisteminin çözüm kümesini oluşturur.
Örnek olarak
denklem sisteminin çözüm kümesini bulup grafiksel olarak yorumlayalım.
Dikkat edilir ise denklemler birbirinin katıdır. Bu durumda aslında iki denklem de aynı doğruyu oluşturur. Bu durumda doğrular çakışıktır ve çözüm kümesi sonsuz elemanlı olur.
Başka bir örnek olarak
denklem sisteminin çözüm kümesini bulup grafikte yorumlayalım.
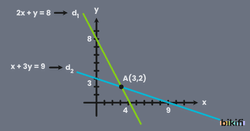
İlk denklemde y bilinmeyenini yalnız bırakırsak y=8-2x olur ve ikinci denklemde y yerine bu değer yazılır ise x+3(8-2x)=9 elde edilir. 5x=15 ve x=3 olur. ÇK={(3, 2)} olur.
Denklemlerin eksenleri kestiği noktaları bulmak için sırasıyla x ve y yerine 0 yazılır.
İlk denklem de x=0 dersek y=8, y=0 dersek x=4 olur. Bu durumda ilk denklemin belirttiği d1 doğrusu (0, 8) ve (4, 0) noktalarından geçer (yeşil doğru).
İkinci denklem için de aynı yöntem uygulanır ise d2 doğrusu (9,0) ve (0, 3) noktalarında eksenleri keser (mavi doğru).
Şekilde de görüldüğü gibi kesişim noktası aynı zamanda çözüm kümesi olan A(3, 2) noktasıdır.
ax+by+m=0 ve cx+dy+n=0 denklem sisteminin belirttiği doğrular ile ilgili aşağıdaki yorumlar yapılabilir.
- ise doğrular çakışıktır ve çözüm kümesinde sonsuz eleman vardır.
- ise doğrular paraleldir ve çözüm kümesi boş kümedir.
- ise doğrular tek noktada kesişir ve çözüm kümesi bir elemanlıdır.
Birinci Dereceden İki Bilinmeyenli Eşitsizlik Sistemleri
a, b, c birer gerçek sayı, a, b sıfırdan farklı olmak üzere
şeklindeki ifadelere birinci dereceden iki bilinmeyenli eşitsizlik denir. Birinci dereceden iki bilinmeyenli denklemlerde olduğu gibi bu eşitsizliğin çözüm kümesi de(x, y) şeklinde sıralı ikiliden oluşur. Eşitsizliği doğru yapan sonsuz sayıda sıralı ikili bulanacağı için çözüm kümesi analitik düzlemde boyalı bölgeler çizilerek gösterilir.
bulunan eşitsizliklerde doğru kesiksiz (düz) çizgi olarak çizilir. < veya > olması durumunda kesikli çizgi olarak çizilir. Eşitsizlik analitik düzlemde çizildiğinde düzlem iki bölgeye ayrılır. Ayrılan bu bölgelerden hangisinin çözüm kümesi olduğunu bulmak için bölgelerden herhangi bir nokta seçilir ve eşitsizlikte yazılır. Eşitsizliği sağlayan noktanın olduğu bölge taranır.
Aşağıdaki örnekte bir çözüm anlatılmıştır.
2x-5y<20 ve eşitsizlik sisteminin çözümünü analitik düzlemde gösteriniz.
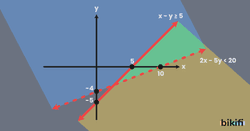
2x-5y<20 için x ve y değerlerine sırasıyla 0 verilerek eksenleri kestiği noktalar bulunur. x=0 için y=-4 ve y=0 için x=10 olur. Sonuç olarak ilk eşitsizlik eksenleri (0,-4) ve (10,0) noktalarında keser. 2x-5y<20 ifadesinde (0,0) noktası yazılırsa 0<20 olur ve eşitsizliği sağladığı görülür. Bu durumda çözüm kümesi olarak doğrunun üst bölgesi alınır fakat eşitlik olmadığı için doğru çözüm kümesine dahil olmaz ve kesikli çizgi ile gösterilir.
için yine aynı yöntem uygulanır ise eşitsizlik (0,-5) ve (5,0) noktalarında eksenleri keser. ifadesinde (0,0) noktası yazılır ise olur ve nokta eşitsizliğin çözüm kümesine dahil değildir. Bu durumda doğrunun alt bölgesi çözüm kümesi olarak alınır ve doğru da çözüm kümesine dahil olduğu için düz çizgi olarak çizilir..
İki eşitsizliğin çözüm kümelerini temsil eden mavi ve kahverengi bölgelerin kesişimi yeşil bölgedir ve eşitsizlik sisteminin çözüm kümesidir.