Bağıntı
Boş küme olmamak şartıyla A ve B herhangi iki küme olmak üzere
kartezyen çarpım kümesinin her bir alt kümesine A’dan B’ye bir bağıntı denir. Bağıntılar genellikle sembolleriyle gösterilir.
Örnek olarak K kümesinden L kümesine tanımlanan bağıntılar aşağıda verilmiştir.
Bir A kümesinden bir B kümesine tanımlanan bağıntısı için
- A kümesinde eşleşmemiş eleman kalmayacak. Bunun nedeni A kümesindeki her girdinin bir karşılığı olmalıdır.
- A kümesindeki her eleman B kümesinde yalnızca bir eleman ile eşleşmelidir çünkü bir girdinin birden fazla karşılığı olmamalıdır.
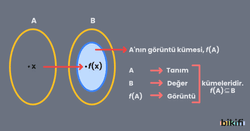
Fonksiyonlarda Değer, Tanım ve Görüntü Kümesi
Yukarıdaki şartları sağlayan bağıntısına A’dan B’ye bir fonksiyon denir. A’dan B’ye tanımlanan fonksiyonu şeklinde gösterilir. Bu gösterimde A kümesine fonksiyonun tanım kümesi, B kümesine fonksiyonun değer kümesi denir.
Bu gösterimde ise x bağımsız değişken, y bağımlı değişken olarak adlandırılır.
A’dan B’ye bir fonksiyonunda A kümesinden B kümesiyle eşleşen elemanlardan oluşan kümeye fonksiyonun görüntü kümesi denir ve ile gösterilir. Görüntü kümesi B kümesinin elemanlarının bazılarından veya tamamından oluştuğu için B kümesi görüntü kümesini kapsar.
Gerekli tanımlamalar yapıldıktan sonra örnek çözerek öğrendiklerimizi pekiştirelim.
Örnekler
Örnek 1: kümesinden kümesine tanımlanan aşağıdaki bağıntılarının fonksiyon olup olmadığını belirleyelim.
Çözüm
- β1 bağıntısında A kümesindeki her elemanın B kümesinde bir karşılığı olduğu için bu bağıntı bir fonksiyondur.
- β2 bağıntısında A kümesinde bulunan “2” elemanının B kümesinde bir karşılığı olmadığı için bu bağıntı bir fonksiyon değildir. Bağıntının fonksiyon olması için tanım kümesindeki(A) her elemanın değer kümesinde(B) bir karşılığı olmak zorundadır.
- β3 bağıntısında A kümesindeki her elemanın B kümesinde aynı elemanla eşleşse bile bir karşılığı bulunduğu için bu bağıntı bir fonksiyondur.
- β4 bağıntısında A kümesindeki her elemanın B kümesinde bir karşılığı vardır fakat “3” elemanının birden fazla karşılığı bulunduğu için bu bir fonksiyon değildir. Bağıntının fonksiyon olabilmesi için tanım kümesindeki(A) her elemanın değer kümesinde(B) yalnızca bir karşılığı olmalıdır.
Örnek 2: fonksiyonu tanımlı olduğu değerlerde olduğuna göre ifadelerini bulalım.
Çözüm
fonksiyonunda x yerine yazacağımız her girdiyi fonksiyonda x gördüğümüz her yere yazılarak yazdığımız girdinin y çıktısını elde ederiz.
Örnek 3: Aşağıdaki fonksiyonların en geniş tanım kümelerini bulalım.
Çözüm
- fonksiyonunda her x için ifadesi bir gerçek sayı olacaktır. Bu durumda x yerine her gerçek sayıyı yazabiliriz. Sonuç olarak fonksiyonunun en geniş tanım kümesini olarak buluruz.
- fonksiyonunda paydanın sıfır olması görüntü kümesinde tanımsız bir ifadeye yol açacağından bu duruma yol açan değer hariç x her gerçek sayıyı alabilir. fonksiyonun paydasındaki ifadesi sıfır olmaması için x değişkeni 4 sayısını alamaz. Sonuç olarak fonksiyonunun en geniş tanım kümesi olarak buluruz.
- fonksiyonunda karekökün içi 0 veya pozitif gerçek sayı olmalıdır. Bu nedenle ifadesi sıfıra eşit veya büyük olmalıdır.
- Buradan fonksiyonunun tanım kümesini olarak buluruz.
Örnek 4: olduğuna göre ifadesini bulalım.
Bu tarz sorularda ilk olarak amacımız fonksiyonunu bulmak olacaktır. Bunun için iki farklı yol izleyebiliriz.
Çözüm 1
İlk çözüm yolu olarak fonksiyonun içindeki ifadeyi başka bir bilinmeyene eşitleyerek x değişkeni yerine koyulması gereken ifadeyi buluruz ve fonksiyonda her x gördüğümüz yere bu ifadeyi yerleştiririz. Bu işlemler bize fonksiyonunu verecektir. Sorunun çözümünde geriye bir tek x yerine istenilen fonksiyonun içindeki ifade yazılarak bu fonksiyonu bulabiliriz.
Çözüm 2
Fonksiyonun giriş değişkenini fonksiyonun içinde oluşturarak fonksiyonunun giriş değişkenine farklı bir ifade yazdığımızda fonksiyonun içinde de aynı ifadeyi yazarak değiştirebiliriz.