Pisagor Teoremi
Bir açısı 90 derece olan üçgene dik üçgen denir. Dik üçgende 90 derecenin karşısındaki kenara hipotenüs, diğer kenarlara dik kenar adı verilir.

Pisagor teoremine göre bir dik üçgende, dik kenarların kareleri toplamı hipotenüsün karesine eşittir.
Aşağıdaki tabloda bazı özel dik üçgenler renk renk ayrılarak verilmiştir. Bu tablo birazda pratiklik kazanmak içindir. Bir dik üçgenin iki kenarı verildiği zaman pisagor teoremi sayesinde üçüncü kenarı bulabiliriz fakat bu tabloyu bildiğimizde dik kenarları 8 ve 15 verilen üçgenin hipotenüsünün direkt 17 olduğunu yazabiliriz. Bu tabloyu soru çözerken yanınızda bulundurup yardım alırsanız bir süre sonra otomatik ezberlemiş olacaksınız.
| 3k | 4k | 5k | 5k | 12k | 13k | 8k | 15k | 17k | 7k | 24k | 25k |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 | 4 | 5 | 5 | 12 | 13 | 8 | 15 | 17 | 7 | 24 | 25 |
| 6 | 8 | 10 | 10 | 24 | 26 | 16 | 30 | 34 | 14 | 48 | 50 |
| … | … | … | … | … | … | … | … | … | … | … | … |
Öklid Teoremi
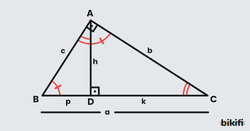
Öncelikle aşağıda verilen görsel üzerinden öklid teoreminin formüllerini verelim, sonra bunların nereden bulunduğunu açıklayalım. Öklid Teoremindeki formüller tamamen üçgenlerde benzerlikten bulunmaktadır.
ABC üçgeninde hipotenüse ait yükseklik çizildiğinde oluşan ABD ve CAD üçgenlerinin açıları eş olduğundan Açı Açı benzerlik kuralına göre olur. Benzer üçgenlerde eş açılar karşısındaki kenarlar orantılı olduğundan
Bir dik üçgende hipotenüse ait yüksekliğin uzunluğunun karesi, bu yüksekliğin hipotenüs üzerinde ayırdığı parçaların uzunluklarının çarpımına eşittir.
- olduğundan
- olduğundan
Bir dik üçgende, bir dik kenarın uzunluğunun karesi, hipotenüse ait yüksekliğin hipotenüste ayırdığı parçalardan kenara yakın olanın uzunluğu ile hipotenüsün uzunluğunun çarpımına eşittir.
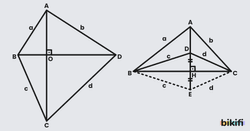
Aşağıdaki şekillerin kenarları arasındaki bağıntıyı öklid ve pisagor teoremleriyle bulabiliriz.
Dik Üçgende Dar Açıların Trigonometrik Oranları
Trigonometri, aynı açılara sahip benzer dik üçgenlerin kenar uzunlukları arasındaki oranların değişmediğini gösterir. Bu oranlara trigonometrik oranlar denir.
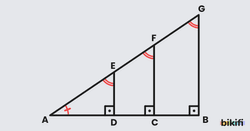
Bunu daha iyi anlamamız için aşağıdaki görselde iç içe geçirilmiş dik üçgenler bulunmaktadır ve hemen aşağısında kenar uzunlukları arasındaki oranların değişmediğini gösteren eşitlikler bulunmaktadır.
Bu yazdığımız oranların sabitliği trigonometride sinüs, kosinüs, tanjant, kotanjant olarak isimlendirilir. Aşağıda ilk olarak bu ifadelerin açıklamaları hemen ardından görselle birlikte kısa gösterimleri verilmiştir.
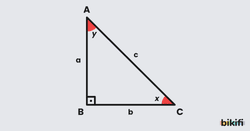
- Bir açının sinüs değeri, dik üçgende açının karşısında bulunan dik kenar uzunluğunun hipotenüs uzunluğuna oranıdır. Kısaca sin ile gösterilir.
- Bir açının kosinüs değeri, dik üçgende açıya komşu olan dik kenar uzunluğunun hipotenüs uzunluğuna oranıdır. Kısaca cos ile gösterilir.
- Bir açının tanjant değeri, dik üçgende açının karşısında bulunan dik kenar uzunluğunun açıya komşu olan dik kenar uzunluğuna oranıdır. Kısaca tan ile gösterilir.
- Bir açının kotanjant değeri, dik üçgende açıya komşu olan dik kenar uzunluğunun açının karşısında bulunan dik kenar uzunluğuna oranıdır. Kısaca cot ile gösterilir.

Tümler Açıların Trigonometrik Oranları
Tümler açılar, toplamları 90 derece olan açılardır. Dik üçgende iki dar açının toplamı da 90 derece olduğundan bu açılar birbirinin tümleridir.
Tümler açılarda birine göre komşu olan kenar diğerine göre karşı kenar olacağından birbirini 90 dereceye tamamlayan açılardan birinin sinüsü diğerinin kosinüsüne, yine birinin tanjantı diğerinin kotanjantına eşittir.
Bu anlattıklarımızı yine görsel üzerinde görelim.
Örnekler
45°-45°-90° Dik Üçgeninde Trigonometrik Oranlar
Aşağıdaki ABC ikizkenar dik üçgeninde
- Pisagor teoreminden olarak bulunur.

Buna göre ABC üçgenindeki A açısının trigonometrik oranları aşağıdaki gibidir.
30°-60°-90° Dik Üçgeninde Trigonometrik Oranlar
Aşağıdaki ABC eşkenar üçgeninin bir köşesinden karşı kenara dik inildiğinde bu yükseklik aynı zamanda açıortay ve kenarortaydır. Buradan 30° – 60° – 90° üçgeni elde edilmiş olur.
- 30° lik açının karşısındaki dik kenarın uzunluğu, hipotenüs uzunluğunun yarısına eşittir.
- Pisagor teoreminden 60° lik açının karşısındaki dik kenarın uzunluğu, 30° lik açının karşısındaki dik kenarın uzunluğunun katına eşittir.

Buna göre 30° ve 60° lik açıların trigonometrik oranları aşağıdaki gibidir.
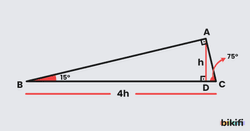
15°-75°-90° Dik Üçgeninde Trigonometrik Oranlar
15°-75°-90° dik üçgeninde hipotenüsün uzunluğu, hipotenüse ait yüksekliğin uzunluğunun 4 katıdır.
|BC| = 4.|AD|
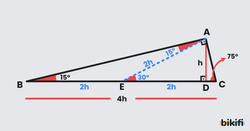
İspat
- ABC dik üçgeninde A açısından 15 derecelik kısım ayrıldığında ikizkenar üçgen elde edilmiş olur.
- Oluşan AED üçgeni bir 30° – 60° – 90° dik üçgenidir.
- AED üçgenine baktığımızda AD yüksekliğine dediğimiz zaman, üçgeninin hipotenüsü olan AE uzunluğu olur.
- ABC üçgeninde A açısını solda 15°, sağda 75° ayırdığımız için AEB ve AEC olmak üzere iki tane ikizkenar üçgen elde etmiş olacağız. Böylelikle olacağından |BC| = 4.|AD| buluruz.
Not: 3. adımda AE uzunluğunu bulduktan sonra dik köşeden indirilen kenarortayın uzunluğu hipotenüsün yarısına eşit olduğundan direkt yorumunu yapabiliriz.
Trigonometrik Oranlardan Biri Belli İken Diğerini Bulma
Trigonometrik oranlardan biri belli iken diğerlerinin bulunması istendiğinde yapılacak iş çok basit. Örnek verirsek bir x° açısının sinüs değeri verilip kotanjant değeri isteniyorsa aşağıdaki adımları izlemeliyiz.
- Bir dik üçgen çizilir ve x° açısı yazılır.
- x° açısının sinüs değerine göre karşı dik kenar ve hipotenüs uzunluğu yazılır.
- Pisagor teoremiyle komşu dik kenar bulunur.
- x° açısının kotanjant değeri için komşu dik kenarı karşı dik kenara böleriz.
Birim Çember ve Trigonometrik Oranlar
Analitik düzlemde merkezi orijin (başlangıç noktası) ve yarıçapı 1 birim olan çembere birim çember denir.

KOP dik üçgeninde Pisagor teoremi uygulandığında denklemi elde edilir.
KOP(üzerinde şapka) açısına göre trigonometrik oranlar yazıldığında elde edilir.
Buna göre birim çember üzerinde bir nokta seçildiği zaman noktanın x değeri kosinüsü, y değeri ise sinüsü verir.