Üçgenin Yardımcı Elemanları: Kenarortay, Orta Dikme ve Yükseklik

Bikifi Instagram'da

Kenarortay

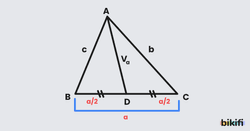
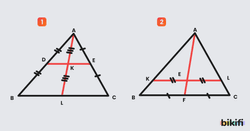
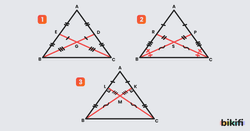
Üçgenin bir köşesinden karşı kenarın ortasına çizilen ve bu kenarı iki eşit uzunluğa bölen doğru parçasına kenarortay denir.

ABC üçgeninde |BD| = |DC| olduğundan [AD] , BC kenarının kenarortayıdır. Bu kenarortayın uzunluğu şeklinde gösterilir.
Benzer şekilde AC kenarının kenarortayı , AB kenarının kenarortayı ile gösterilir.

Ağırlık Merkezi

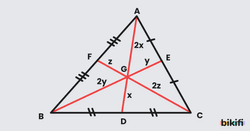
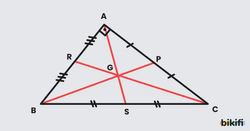
Kenarortaylar üçgenin içinde bir noktada kesişir. Bu noktaya üçgenin ağırlık merkezi denir.

• G noktası üçgenin ağırlık merkezidir.
• Ağırlık merkezi kenarortayları köşeye 2 birim, kenara 1 birim oranında keser.
• |AG|=2.|GD| , |BG|=2.|GE| , |CG|=2.|GF| olur.

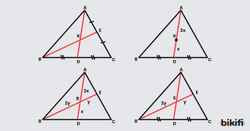
Bir üçgende ağırlık merkezini bulmak için 3 kenarortayın olması gerekmeyebilir. Aşağıdaki durumlarda da ağırlık merkezini bulduğumuzdan emin olabiliriz.

1. 2 kenarortayın kesiştiği nokta
2. Bir kenarortayı 2’ye 1 oranında ayıran nokta
3. Üçgenin içinde kenarortay olduğu bilinmeyen fakat birbirini 2’ye 1 oranlayacak şekilde doğruların kesiştiği nokta
4. Üçgenin içindeki bir doğrunun([BE]), bir kenarortayın([AD]) kendisini 2’ye 1 oranında kestiği nokta

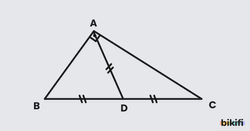
Ayrıca bir dik üçgende hipotenüse ait kenarortayın uzunluğu, hipotenüsün uzunluğunun yarısına eşittir.

ABC dik üçgeninde [AD] , hipotenüse ait kenarortay ise

|BD|=|DC|=|AD| olup |BC|=2.|AD| olur.

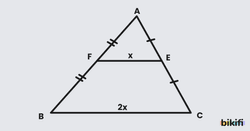
Orta Taban

Bir üçgenin iki kenarının orta noktalarını birleştiren doğru parçasına orta taban denir.

ABC üçgeninde [DE] orta taban ise [DE] // [BC] ve |BC| = 2.|DE| olur.

1. Bir üçgende tepe noktasından tabana indirilen her doğru parçası orta taban tarafından iki eş parçaya ayrılır.
2. Bir üçgende tabana indirilen kenarortay, orta taban da dahil tabana paralel çizilen tüm doğru parçalarını iki eş parçaya ayırır.

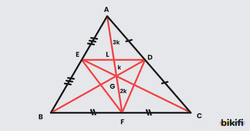
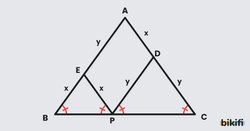
Bir üçgende ağırlık merkezinin kenarortayı köşeden 2 birim, kenardan 1 birim oranında, orta taban ise bir kenarortayı iki eş parçaya ayırdığını öğrendik.

Yukarıdaki üçgende kenarortaylar ve bir orta taban birlikte çizilmiştir.

• [AF] kenarortayının uzunluğunu 6k olarak aldığımızda ağırlık merkezi kenarortayı 2’ye 1 oranda böleceğinden, [AG]= 4k ve [GF]=2k olarak buluruz.
• Orta taban [AF] kenarını iki eş parçaya böleceğinden, [AL]=3k ve [LF]=3k olarak buluruz.
• [LF]= 3k için [GF]=2k ise [LG]=k olur.
• Sonuç olarak bir kenarortay köşeden kenara doğru sırasıyla 3,1,2 oranında bölünür.

Kenarortay Uzunluğu

ABC üçgeninde a, b ve c kenarlarına ait kenarortaylar sırasıyla olmak üzere üçgenin kenarları ile kenarortayları arasında

• bağlantıları vardır.

Bu bağlantılar taraf tarafa toplanıp düzenlenirse

bağlantısı bulunur.

ABC dik üçgeninde

• ve
• olmak üzere
• olur.

Orta Dikme

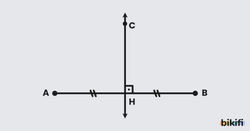
Bir doğru parçasının orta noktasından geçen ve doğru parçasına dik olan doğruya orta dikme doğrusu denir.

Yukarıdaki şekilde CH doğrusu, AB doğru parçasının orta dikmesidir.

Üçgende Kenar Orta Dikme

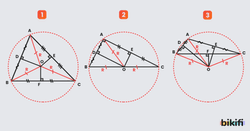
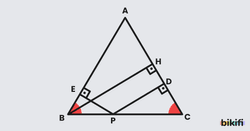
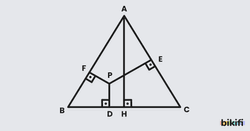
Bir ABC üçgeninde A, B ve C noktalarından geçen çember üçgenin çevrel çemberi olarak isimlendirilir.

Bir üçgenin kenar orta dikmeleri tek noktada kesişir. Bu nokta, üçgenin çevrel çemberinin merkezidir.

Aşağıdaki görsellerde görüldüğü gibi bir üçgenin kenar orta dikmelerinin kesiştiği noktanın üçgenin köşelerine olan uzaklıkları eşittir ve bu uzaklık üçgenin çevrel çemberinin yarıçapıdır.

ABC üçgeninde çevrel çemberin merkezi O, yarıçapı R ise |AO| = |BO| = |CO| = R birimdir.

Üçgenin çeşidine göre çevrel çemberinin merkezi için 3 farklı durum vardır.

1. Dar açılı üçgenin çevrel çemberinin merkezi, üçgenin iç bölgesindedir.
2. Dik üçgenin çevrel çemberinin merkezi, hipotenüsün orta noktasıdır.
3. Geniş açılı üçgenin çevrel çemberinin merkezi, üçgenin dış bölgesindedir.

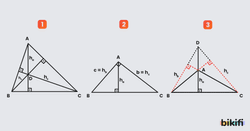
Yükseklik

Üçgenin bir köşesinden karşısındaki kenara çizilen dikmeye üçgenin o kenarına ait yüksekliği denir. Bir ABC üçgeninin a, b, c kenarlarına ait olmak üzere üç yüksekliği vardır. Bir üçgende yükseklikler tek noktada kesişir. Bu noktaya üçgenin diklik merkezi denir.

Üçgenin çeşidine göre diklik merkezi için üç farklı durum vardır.

1. ABC üçgeni dar açılı üçgen ise diklik merkezi üçgenin iç bölgesindedir. Diklik merkezi D noktasıdır.
2. ABC üçgeni dik üçgen ise diklik merkezi üçgenin dik köşesidir. A noktası aynı zamanda diklik merkezidir.
3. ABC üçgeni geniş açılı üçgen ise diklik merkezi üçgenin dış bölgesindedir. Diklik merkezi D noktasıdır.

İkizkenar Üçgenin Yardımcı Elemanları

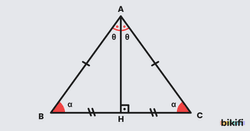
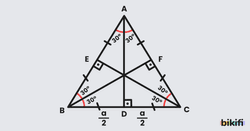
İkizkenar üçgenlerde eşit olmayan kenara indirilen dikme üçgeni iki eş üçgene ayırır.

1. İkizkenar üçgende eşit kenarlara ait kenarortay uzunlukları birbirine eşittir.
2. İkizkenar üçgende eşit açılara ait açıortay uzunlukları birbirine eşittir.
3. İkizkenar üçgende eşit kenarlara ait yükseklik uzunlukları birbirine eşittir.

Her birinde sağ ve sol tarafta simetrik bir yapı oluşur.

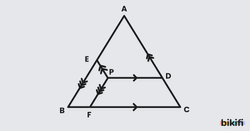
İkizkenar üçgende taban üzerindeki herhangi bir noktadan eşit kenarlara çizilen paralellerin uzunlukları toplamı, eşit kenarlardan birinin uzunluğuna eşittir.

İkizkenar üçgende taban üzerindeki herhangi bir noktadan eşit kenarlara çizilen dikmelerin uzunlukları toplamı, eşit kenarlara ait yüksekliğe eşittir.

Eşkenar Üçgenin Yardımcı Elemanları

Eşkenar üçgende üç kenara ait yükseklik ve kenarortay uzunlukları ile üç açıya ait açıortay uzunlukları eşittir.

Eşkenar üçgenin iç bölgesinde veya kenarlarının üzerinde alınan herhangi bir noktadan kenarlara çizilen paralellerin uzunlukları toplamı, eşkenar üçgenin bir kenar uzunluğuna eşittir.

Eşkenar üçgenin iç bölgesinde veya kenarlarının üzerinde alınan herhangi bir noktadan kenarlara indirilen dikmelerin uzunlukları toplamı, eşkenar üçgenin yüksekliğine eşittir.