Üçgenlerde Temel Alan Bağıntısı
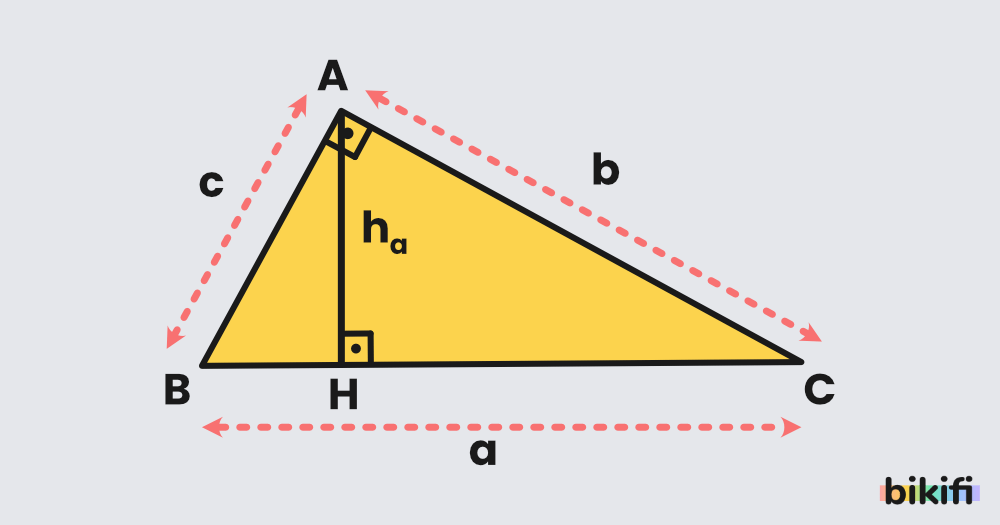
Bir üçgensel bölgenin alanı, bir kenar uzunluğu ile o kenar uzunluğuna ait yüksekliğin uzunluğunun çarpımının yarısına eşittir. A, B, C köşelerinden oluşan üçgensel bölgenin alanı biçiminde gösterilir.
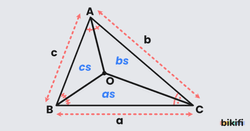
Dar Açılı Üçgende Alan
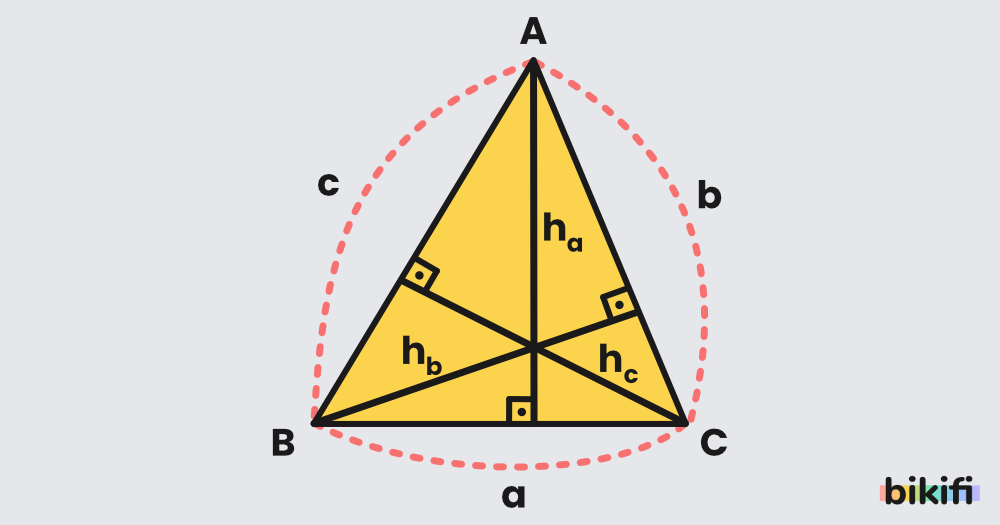
Dik Üçgende Alan
Dik üçgensel bölgenin alanı, dik kenar uzunluklarının çarpımının yarısının alınması ile bulunur. Eğer hipotenüse ait yükseklik biliniyorsa taban ile yükseklik çarpımının yarısı da alınabilir.
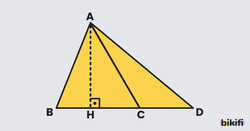
Geniş Açılı Üçgende Alan
Geniş açılı üçgenlerde [AB] ve[BC] kenarlarına ait yükseklikler üçgenin dış bölgesindedir.

Üçgenlerde Alan İlişkileri
Bu bölümde iki veya daha fazla üçgenin taban ve yükseklikleri arasında karşılaştırma yaparak alanları arasında orantı kuracağız.
Aşağıdaki şekilde d1//d2 olmak üzere ABC üçgeninin A noktası hareket ettirildiğinde oluşan A’BC üçgeninin alanı değişmez. Bu üçgenlerin tabanları ve yükseklikleri aynı uzunluktadır.

Yükseklikleri eşit olan üçgenlerin alanları oranı bu yüksekliklere ait taban uzunlukları oranına eşittir. Benzer şekilde tabanları eşit olan üçgenlerin alanları oranı yükseklikleri oranına eşittir.
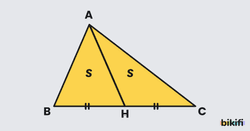
ABC ve ACD üçgenlerinin yükseklikleri eşit olduğu için alanları oranı taban uzunluklarının oranına eşittir.
Yine aynı mantıkla kenarortay, üçgeni alanları eşit olan iki parçaya ayırır.
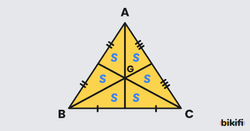
Ağırlık merkezi üçgenin alanını 6 eşit parçaya ayırır.
Heron Alan Formülü
Bir üçgenin bütün kenar uzunluklarını bilmemize rağmen herhangi bir kenara ait yüksekliği bulamıyorsak bu durumda üçgenin alanını Heron Alan Formülü sayesinde bulabiliriz.
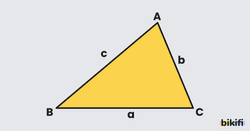
Kenar uzunlukları a, b, c olan üçgenin çevre uzunluğunun yarısı olmak üzere
bağıntısı ile bulunur.
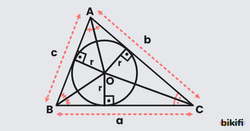
İç Teğet Çember Yardımıyla Alan Bulma
ABC üçgeninin çevresi ve iç teğet çemberinin yarıçapı biliniyorsa üçgenin alanı hesaplanabilir. ABC üçgeninin yarıçapı r olsun.
ABC üçgenini aşağıdaki gibi üç parça olarak düşünürsek her bir üçgenin yüksekliği r, her bir taban uzunluğu ise a, b, c olacaktır. Bu üçgenlerin alanlarını bulalım.
Bu üçgenlerin alanları toplamı ABC üçgeninin alanını verir.
Sonuç olarak bir üçgenin çevresinin yarısını, o üçgenin içteğet çemberinin yarıçapıyla çarparsak üçgenin alanını elde ederiz.
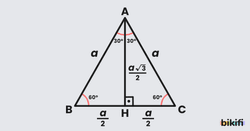
Eşkenar Üçgenin Alanı
Eşkenar üçgende bir köşeden karşısındaki kenara dik inildiğinde 30° – 60° – 90° dik üçgeni oluşacağından
Bir kenara ait yükseklik olarak buluruz.
Benzer Üçgenlerin Alanı
Benzer iki üçgenin alanları oranı benzerlik oranının karesine eşittir.
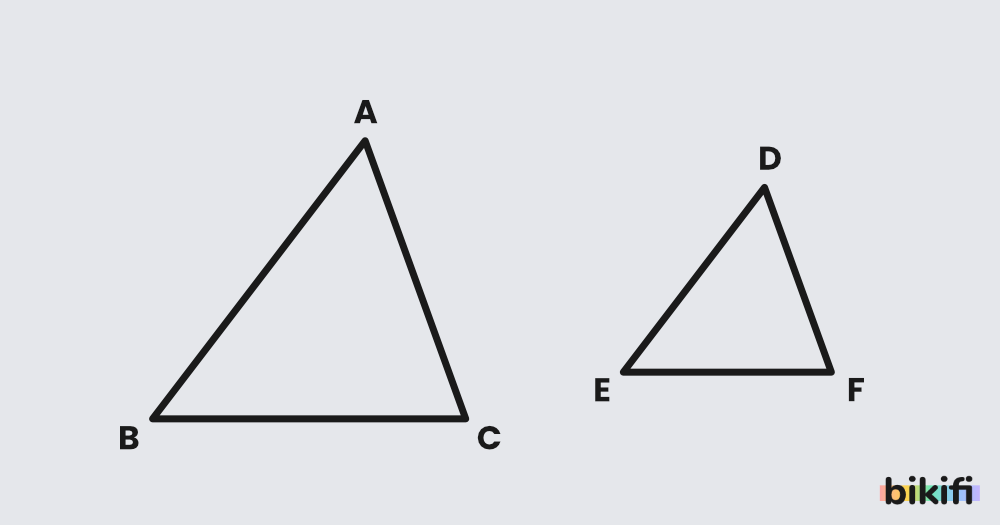
ve benzerlik oranı ise
olur.
Bu ifadenin doğruluğu aşağıdaki gibi gösterilebilir.

ve benzerlik oranı olduğundan