Paralel İki Doğrunun Bir Kesenle Yaptığı Açılar

- Ters Açılar: Kesişen iki doğrunun oluşturduğu açılardan karşılıklı duran açılara (komşu olmayanlara) ters açılar denir. 1 ile 3, 2 ile 4, 5 ile 7, 6 ile 8 ters açılardır ve ölçüleri birbirine eşittir. Bu durumun diğer adı “U kuralı” olarak geçer.
- İç Ters Açılar: Bir doğruyu kesen paralel doğruların iç kısmında kalan ve farklı yönlere bakan açılara iç ters açılar denir. 3 ile 5, 4 ile 6 iç ters açılardır ve ölçüleri birbirine eşittir. Bu durumun diğer adı “Z kuralı” olarak geçer. Z harfini oluşturan şekillerde aradaki açılar birbirine eşit oluyor ve biri için verilen açıyı direkt diğerine de yazabiliyoruz.
- Dış Ters Açılar: Bir doğruyu kesen paralel doğruların dış kısmında kalan ve farklı yönlere bakan açılara dış ters açılar denir. 1 ile 7, 2 ile 8 dış ters açılardır ve ölçüleri birbirine eşittir.
- Yöndeş Açılar: Açıyı oluşturan iki ışının her açı için aynı yöne baktığı açılara yöndeş açılar denir. 1 ile 5, 2 ile 6, 3 ile 7, 4 ile 8 yöndeş açılardır ve ölçüleri birbirine eşittir.
- Karşı Durumlu Açılar: Bir doğruyu kesen paralel doğruların iç kısımlarında kalan ve aynı yöne bakan açılara karşı durumlu açılar denir. 4 ile 5, 3 ile 6 karşı durumlu açılardır ve bu açıların ölçüleri toplamı her zaman 180 derecedir.
Paralel İki Doğru Kuralları
Yukarıda anlatılan U ve Z kuralına ek olarak işlem yapmamızı kolaylaştıran M kuralı da bulunmaktadır. Aynı zamanda paralel iki doğru arasına yerleştirilen açı sayısına bakarak iç açıları toplamını da hesaplayabiliyoruz.
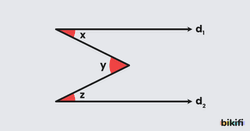
M Kuralı
Yandaki görselde görüldüğü gibi iki paralel doğru arasında çizilen farklı yönlere bakan dar açılar için sağa ve sola bakan açılar olarak ayırırız. Sağa bakan açıların toplamı sola bakan açıya eşit olur. Buradaki mantık ortada bulunan açıdan geçen diğer doğrulara paralel bir doğru daha çizilirse açısı iki parçaya bölünmüş olacak ve iç ters açılar durumundan(Z kuralı) y açısının üst kısmını x, alt kısmını ise z açısı oluşturacaktır. Bu durumda;
olacaktır.
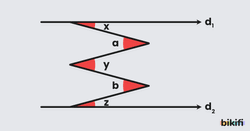
Çoklu M Kuralı
Yukarıdaki şekilde ise paralel doğrular arasında farklı yönlere bakan çok sayıda dar açı var fakat yukarıdaki durumla mantık olarak aynıdır. Yine sağa bakan ve sola bakan açılar olarak ayırıp toplamlarını birbirine eşitleyebiliriz.
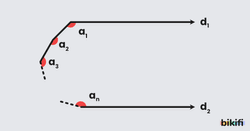
Açı Sayısına Göre İç Açıları Toplamını Bulmak
Yukarıdaki gibi iki paralel doğru arasında çizilen bir geniş açı için içeride oluşan açı sayısının bir eksiği ile 180°’nin çarpımı içerideki açıların toplamını verecektir. Buradaki mantık açısının üzerinden geçecek ve diğer doğrulara paralel yeni bir doğru çizdiğimiz zaman y açısı ikiye bölünür. Karşı durumlu açılar kuralından y açısının üstte kalan kısmıyla x açısının toplamı 180 dereceyi verir, yine aynı mantıktan y açısının altta kalan kısmıyla z açısının toplamı da 180 dereceyi verir. Sonuç olarak bu üç açının toplamı 2 tane 180 dereceyi verdi yani açı sayısının bir eksiği kadar 180 derece.
Yukarıdaki şekilde ise paralel doğrular arasında aynı yöne bakan çok sayıda geniş açı var. Bu durum yukarıdakinden farksızdır. genel formül ise aşağıdaki gibi ifade edilebilir.
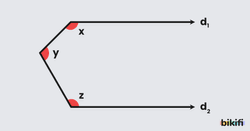
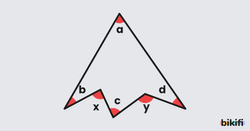
Bir Noktada Kesişen Doğrulardaki Açı Kuralı
İki paralel yerine bir noktada birleşen doğrular olduğunda normalde farklı yöne bakan açıların toplamı eşit olurdu fakat burada doğruların birleştiği noktadaki açı () ters yöne eklenir. Buradaki mantık ise açılarının oldukları noktalardan iki dikey doğru çizildiğinde açısı iç ters açılar kuralından (Z kuralı) bir kısmı açısının üstüne, bir kısmı da açısının üstüne gidecek. Sonuç olarak bu taşımadan sonra iki paralel arasında farklı yönlere bakan dar açılar oluşmuş olacak ve ona göre açıları eşitlerken açısına eklenecektir.
- olduğuna göre;
Açı Kurallarıyla İlgili Soru Çözüm Tavsiyesi
Sorularda paralel doğrular gördüğünüz zaman iç ters, dış ters ve karşı durumlu açılar kurallarını kullanmaya çalışın. Bu kurallar sürekli karşınıza çıkacak ve siz bunları kafanıza oturtursanız büyük rahatlık yaşarsınız. Size verilen açıları bu kuralları uygulayarak verilmeyen yerdeki açılardan yazabildiğinizi yazıp sonra soru üzerinde düşünün. Kolaylıkla bulacağınıza eminim.