Kümelerin Kartezyen Çarpımı ve Bağıntı

Sıralı İkili Kavramı

a ve b birer nesne olmak üzere (a, b) şeklinde gösterilen ifadeye sıralı ikili veya ikili denir. a ve b sayı olmak zorunda değildir. a ya bu sıralı ikilinin birinci bileşeni, b ye ikinci bileşeni denir.

Bu nesnelerin daha çok olduğu durumlarda mevcuttur. (a, b, c) şeklinde sıralı üçlüler tanımlanabilir. Bu durumda genelleme yapacak olursak a₁, a₂, a₃ , …… a_n-1 , a_n elemanlarından oluşan ( a₁, a₂, a₃ , …… a_n-1 , a_n ) ifadesine sıralı n denir.

Sıralı İkililerin Eşitliği

İki sıralı ikilinin eşit olması durumu aynı sıradaki elemanlarının birbirine eşit olması ile sağlanır.

(a, b) = (c, d) (a=c ve b=d) olur.

Kartezyen Çarpım

Boş küme olmayan iki farklı A ve B sıralı ikilisi var olsun. İlk bileşeni A kümesinden ikinci bileşeni B kümesinden alınarak oluşturulan tüm sıralı ikililerin kümesine A ve B kümelerinin kartezyen çarpım kümesi veya A kartezyen B denir.

A x B ortak özellik yöntemiyle A x B = {(x, y) | x A ve y B} şeklinde yazılabilir. A = B durumunda A x A elde elde edilebilir ve bu küme A² şeklinde ifade edilir.

Kartezyen Çarpımın Özellikleri

A={a₁, a₂, a₃}, B = {b₁ , b₂ , b₃} kümeleri verilsin. Bu kümelerin kartezyen çarpımı aşağıdaki gibidir.
A x B = {(a₁, b₁), (a₁, b₂), (a₁, b₃), (a₂, b₁), (a₂, b₂), (a₂, b₃), (a₃, b₁), (a₃, b₂), (a₃, b₃)}
Yukarıdaki tüm ikililer, kartezyen çarpım kümesinin elemanlarıdır. Bu kümenin eleman sayısı s(A x B) = s(A). s(B) = k.n olarak bulunur. s(A x B) = s(B x A) = s(A). s(B) olur.
Kartezyen çarpımının değişme özelliği yoktur.
A x B ={(x, y) | x A ve y B}
A x B ={(y, x) | y B ve x A}
x y için (x, y) (y, x) olduğuna göre A x B kümesinin elemanları ile B x A kümesinin elamanları eşit değildir. Bu durumda A B için A x B B x A olur.
Kartezyen çarpım işleminin birleşim, kesişim ve fark işlemleri üzerine sağdan veya soldan dağılma özelliği vardır.
A x (B C) = (A x B) (A x C)

Kartezyen Çarpımının Grafiği

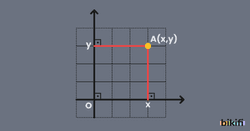
R² = R x R ={(x,y) | x R ve y R} kümesinin belirttiği noktaların oluşturduğu düzleme kartezyen koordinat sistemi (analitik düzlem) denir.

A(x, y) R² ise bu noktaların birinci bileşenine noktaların apsisi, ikinci bileşenine noktaların ordinatı denir. (x, y) ikilisine A’nın koordinatları adı verilir.

A noktasına karşılık gelen sıralı ikili (x y) ise x değerine A nın apsisi, y ye A nın ordinatı denir. A x B = {(x, y) | x A ve y B} kümesinin elemanlarının analitik düzlemde aşağıdaki gibi gösterimiyle oluşan şekle A x B nin grafiği denir.

Bağıntı

İki kavram arasında kurulan ilişki ya da bağ bağıntı olarak tanımlanır.

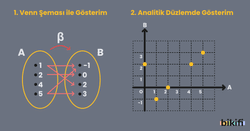
A ve B boş kümeden farklı iki küme olmak üzere, A x B nin her alt kümesine A dan B ye bir bağıntı denir. …. ile gösterilir. A x B olur.

Burada s(A)=m, s(B)=n, s(A x B)= m.n olduğuna göre A dan B ye tanımlanabilecek bütün bağıntıların sayısı 2^m.n olarak hesaplanır.

Bir bağıntının elemanlarının analitik düzlemde işaretlenmesiyle elde edilen şekle bağıntının grafiği denir.

Bir bağıntısının elemanları olan bütün ikililerin bileşenlerinin yerleri değiştirilerek elde edilen bağıntıya bağıntısının tersi denir. ile gösterilir.

(x, y) ve
olur.