Bir Doğrunun Eğim Açısı ve Eğimi
Bir doğrunun x ekseniyle yaptığı pozitif yöndeki açının tanjantına doğrunun eğimi denir. Doğrunun x ekseniyle yaptığı açının kendisi ise eğim açısıdır. Doğrunun eğimi m ile gösterilir. Bir doğru x ekseniyle α açısı yapıyorsa bu doğrunun eğimi için aşağıdaki ifadeyi yazabiliriz.
Doğrunun eğimini bulurken eğim açısının tanjantını almamız karşıdaki yükselmenin yandaki genişlemeye bölmemiz anlamına gelir. Bu da aslında doğrunun belli bir aralığında y eksenindeki değişimi x eksenindeki değişime bölmemiz demektir. Şimdilik bu genel mantığı anladıysak bir sonraki başlıkta daha detaya gireceğiz.
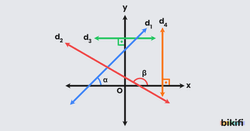
Doğrunun eğim açısını doğru belirlemek çok önemli. Bize bir açı verildiğinde bu açının nereye ait olduğunu bilmemiz gerekir. Doğrunun x ekseniyle kesiştiği noktayı orijin gibi kabul edersek, x ekseninden başlayarak pozitif yöne doğru(saat yönünün tersi) belirlediğimiz doğruya kadar yaptığı açı bize eğim açısını verir. Aşağıdaki görsellerde örnek doğrular ve eğim açıları(α ve β) gösterilmiştir.
Doğrunun eğim açısına göre eğiminin işareti değişmektedir. Aşağıda belli eğim açısı veya açı aralıkları üzerinden eğimin durumlarına göz atacağız.
Not: Eğim açısı 0° ile 180° arasında bir değer alır. Eğim açısı için dar açı diye bahsediliyorsa 0° ile 90° arası, geniş açı diye bahsediliyorsa 90° ile 180° arasında bir değer olduğu anlaşılır. Eğim açısının 180°’ye kadar olmasının sebebi ise 180°’ye vardığımızda doğru tam yatay konuma gelir ve aslında bu 0°’yle aynı durumdur. Yani bir doğruyu çevirmeye başladığımızda her 180°’de bir sıfırlanacaktır.
- d1 doğrusu için:α açısı bir dar açıdır. Dar açılar için tanjant değeri pozitif olacağı için eğim pozitiftir. Yani analitik düzlemde bir doğruya baktığımızda sağa doğru yatık bir şekilde duruyorsa eğimi için direkt pozitif diyebiliriz.
- d2 doğrusu için:β açısı bir geniş açıdır. Geniş açılar için tanjant değeri negatif olacağı için eğim negatiftir. Aynı şekilde bir doğruyu incelediğimizde bu sefer sola yatık bir şekilde duruyorsa bu sefer eğimi negatif yorumunu yapabiliriz.
- d3 doğrusu için: Bu doğru x eksenine paraleldir ve eğim açısı 0° olarak alınır. Tanjantın 0° için değeri sıfıra eşit olacağı için bu durumda eğim sıfırdır.
- d4 doğrusu için: Bu doğru y eksenin paraleldir. Bu nedenle eğim açısı 90° olur. Tanjantın 90° için değeri ise tanımsızdır. Bu durumda y eksenine paralel doğruların eğimi tanımsızdır.
İki Noktası Verilen Doğrunun Eğimi
Analitik düzlemde belli iki nokta üzerinden geçen sadece bir doğru vardır. Bu doğrunun eğimini verilen iki nokta sayesinde bulabiliriz.
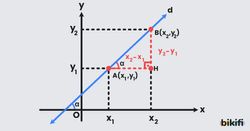
Bir d doğrusu üzerinde A(x1,y1) ve B(x2,y2) noktaları verilmiş olsun. Bu doğrunun x ekseniyle yaptığı açıya α açısı diyelim.
Bu d doğrusunun eğimini bulurken aslında bulmamız gereken şey α açsının tanjantını bulmaktır. Dik üçgendeki bir açının tanjantını karşı bölü komşu yaparak bulduğumuzu öğrenmiştik. Yukarıdaki görselde d doğrusu, A ve B noktaları, α açısı ve noktaların yatay ve dikeydeki uzantıları gösterilmiştir. Böylece ortada bir açısı α olan bir dik üçgen oluşmuştur. Bu α açısının tanjantını bulmak istediğimizde karşı dik kenarı komşu dik kenara böleceğiz. Burada bulunan karşı dik kenar aslında B noktasının y değerinden A noktasının y değerinin çıkarılmasıyla bulunur. Aynı şekilde komşu dik kenar B noktasının x değerinden A noktasının x değerinin çıkarılmasıyla bulunur.
Eğimi bulurken her zaman grafikte böyle görmeyeceğiz fakat bu yöntem doğrunun eğimini bulurken hep aynıdır. Her zaman y değerleri farkını x değerleri farkına bölerek bulabiliriz. Burada dikkat etmemiz gereken nokta y değerleri için hangi noktanın değerinden diğerini çıkartıyorsak x değerleri için de aynı şekilde yapmalıyız. Yani A noktasının değerlerinden B noktasınınkileri çıkartabiliriz veya tam tersini uygulayabiliriz fakat A noktasının y değerinden B noktasının y değerini çıkartıp diğer taraftan B noktasının x değerinden A noktasının x değerini çıkartıp bölme işlemi yapamayız.
Örnek: Analitik düzlemde A(-3,1) ve B(7,-4) noktalarından geçen doğrunun eğimi kaçtır?
Verilen bu noktaların y değerleri farkını x değerleri farkına bölerek eğimi bulalım. A noktasının değerlerinden B noktasınınkileri çıkartarak bulalım. Tam tersi şekilde de bulunabilir.
Böylece A ve B noktalarından geçen doğrunun eğimini -2 buluruz.
Örnek: Analitik düzlemde A(-5,4), B(k,8) ve C(6,2k) noktaları veriliyor. A ve B noktalarından geçen doğrunun eğimi mAB=2 olduğuna göre B ve C noktalarından geçen doğrunun eğimi mBC kaçtır?
Öncelikle A ve B noktalarından geçen doğrunun eğimini hesaplayarak bize verilen eğim değerine eşitleyelim ve k değerini bulalım.
k değerini bulduğumuza göre B ve C noktalarında yerine koyarak B(-3,8) ve C(6,-6) noktalarını elde ederiz. Bu noktalardan geçen doğrunun eğimini hesaplayabiliriz.
Birbirine Paralel ya da Dik Olan Doğruların Eğimleri Arasındaki Bağıntılar
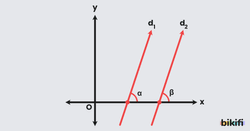
Birbirine paralel olan doğrular x ekseniyle aynı açıyı yaptıkları için eğimleri aynı olur.
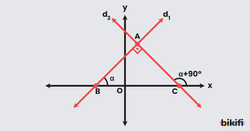
Birbirine dik olan doğrular da bir doğrunun x ekseniyle yaptığı açı diğer diğer doğrunun açısından 90° fazla olur.
İlk olarak d1 doğrusuna baktığımızda eğimi için m1=tanα ifadesini yazabiliriz. d2 doğrusunu incelediğimizde x ekseniyle yaptığı açı α+90° olduğu için eğimini m2=tan(α+90°) olarak buluruz. tan(α+90°) ifadesini trigonometriyi kullanarak yalnızca α açısı kalacak şekilde düzenlersek
sonucuna varırız. Şimdi iki eğimi birlikte inceleyelim.
Birbirine dik olan iki doğrunun eğimlerinin çarpımının -1 olduğunu buluruz.
Örnek: Analitik düzlemdeki ve eğimlere sahip iki doğru birbirine diktir. Bu durumda k sayısını bulalım.
Birbirine dik olan doğruların eğimlerinin çarpımı -1’e eşit olduğu için verilen eğimleri çarparak -1’e eşitlediğimizde çıkan denklemde k sayısına ulaşabiliriz.