Çarpanlara Ayırma

Çarpanlara ayırma, bir polinomun kendisini oluşturan bileşenlerin çarpımı şeklinde yazılmasına denir. Çarpanlara ayırmadaki temel amaç verilen ifadeyi daha küçük yapılara ayırarak yorumlamayı kolaylaştırmaktır. Çarpanlara ayırma işlemi matematikte sıklıkla kullanıldığı için, matematiksel yorum süresini ve işlem yeteneğini artıran önemli bir uygulamadır. Çarpanlara ayırma işlemi için aşağıdaki yöntemler kullanılabilmektedir.

Ortak çarpan parantezine alarak çarpanlarına ayırma
Gruplandırarak çarpanlarına ayırma
Özdeşliklerden yararlanarak çarpanlarına ayırma
Değişken değiştirerek çarpanlarına ayırma
Üç terimli ifadeleri kullanarak çarpanlarına ayırma
Terim ekle/çıkar yöntemiyle çarpanlarına ayırma

Ortak Çarpan Parantezine Alma Yöntemi

Bir ifade çarpanlarına ayrılırken ifadenin her teriminde ortak çarpan varsa bu ifade ortak çarpan parantezine alınarak çarpanlarına ayrılır.

Örnekler

ay+by = y(a+b)
4y²+ 20y = 4y(y+5)
4x²+ 20x + 3xy +15y
- = 4x(x+5) + 3y(x+5)
- = (x+5) * (4x+3y)
bx+ by + b = b(x+y+1)
(3x-5).(p-y)+(10x+4).(y-p)
- = (3x-5).(p-y)+(10x+4).(-1)(p-y)
- = (3x-5).(p-y)+(-10x-4).(p-y)
- = (3x-5-10x-4).(p-y)
- = (-7x-9).(p-y)
2(a-b)²+ (3a-2b).(b-a) + 10(b-a)
- = 2(b-a)²+ (3a-2b).(b-a) + 10(b-a)
- = (b-a)[2(b-a) + (3a-2b)+10]
- = (b-a)[2b-2a + 3a-2b+10]
- = (b-a)(a+10)

📌İpuçları

Ortak çarpan parantezine almayı kolaylaştırmak için aşağıdaki dönüşümleri kullanabilirsiniz.

x-y = -(y-x)
(x-y)² = (y-x)²
(x-y)³ = -(y-x)³

Gruplandırarak Çarpanlara Ayırma Yöntemi

Verilen ifadenin hepsine ortak parça her zaman bulunamayabilir. Böyle bir durumda ortak parçaları kendi içerisinde gruplandırabiliriz.

ax + ay + bx+ by
- = a(x+y) + b(x+y)
- = (a+b)(x+y)
a³+a²-a-1
- = a²(a+1)-1(a+1)
- = (a²-1)(a+1)
- = (a+1)(a-1)(a+1)
- = (a+1)²(a-1)

✍ Örnek Soru Tipi

b-k = 8
b+f = 12
olduğuna göre, işleminin sonucu kaçtır?

🖋 Çözüm

b-k = 8 ve b+f = 12 olduğu bilindiğine göre, b-k=8 denklemi (-1) ile çarpılarak k-b=-8 elde edilir.
k-b=-8 ve b+f=12 taraf tarafa toplanırsa,
k+f=4 elde edilir.
işlemi sadeleştirilirse;
k+f = 4 ve k-b=-8 olduğu bilindiğine göre
4*(-8) = -32 olarak bulunur

Özdeşliklerden Yararlanarak Çarpanlara Ayırma Yöntemi

Çarpanlara ayırma için bilinen özdeşliklerden yararlanılabilir. Bu özdeşlikler; iki kare farkı, tam kare, iki küp farkı, iki küp toplamı ve tam küp ifadelerdir.

Tam Kare İfadeler

Tam kare ifadeler şu şekilde özetlenebilir:

✍ Örnek Soru Tipi – 1

b+k = 8
b²+k² = 24
olduğuna göre, b.k işleminin sonucu kaçtır?

🖋 Çözüm

b+k = 8 ifadesinin karesi alınırsa;
Elde edilen ifadede b²+k² = 24 bilgisi yerine yazılırsa;
elde edilir.

✍ Örnek Soru Tipi – 2

ifadesinin sonucu kaçtır?

🖋 Çözüm

306 = b kabul edilip verilen ifade düzenlenirse;
bulunur.

✍ Örnek Soru Tipi – 3

b-k = 8
b.k = 4
olduğuna göre, b+k işleminin pozitif değeri kaçtır?

🖋 Çözüm

Soruda istenen işlemin sonucu x’e eşit olsun.
- x=b+k
b-k = 8 ifadesinin karesi alınır.
- b²-2bk+k²=64
Elde edilen denkleme b.k=4 bilgisi eklenir.
- b²-2.4+k²=64
- b²-8+k²=64
- b²+k²=72
Soruda istenen x=b+k ifadesinin karesi alınır.
- x²=b²+2bk+k²
2. adımda bulunan ifade ile soruda verilen b.k verisi eklenirse;
- x²=72+2.4
- x²=72+8=80
- x = =

✍ Örnek Soru Tipi – 4

olduğuna göre, işleminin sonucu kaçtır?

🖋 Çözüm

Soruda verilen işlemin karesi alınır.

🚀 İpucu

(x+y)²-(x-y)²=((x+y)+(x-y)).((x+y)-(x-y)) =2x.2y = 4xy

İki Kare Farkı

✍ Örnek Soru Tipi – 1

olduğuna göre, 7b+2k işleminin sonucu kaçtır?

🖋 Çözüm

Öncelikle ilk ifade çarpanlarına ayrılır
3b+k=2 olduğu bilindiğine göre yukarıdaki denklemde yerine konulur
3b-k = 16 olarak bulunur.
3b+k = 2 olduğu bilindiğine göre, taraf tarafa toplama yapılarak
- 6b=18 => b=3 olarak bulunur.
b=3 herhangi bir denklemde yerine yazılırsa
- 3(3)+k=2 => k=-7 olarak bulunr.
Bulunan değerler 7b+2k denklemine yazılarak sonuç bulunur
- 7(3)+2(-7) = 7

✍ Örnek Soru Tipi – 2

olduğuna göre, işleminin sonucu kaçtır?

🖋 Çözüm

Öncelikle soruda istenen ifade çarpanlarına ayrılır;
Soruda verilen ifadeler yerine yazılırsa;
Soruda verilen ve ifadeleri taraf tarafa toplanır
3. adımda bulunan ifade 2. adımda bulduğumuz sonuca eklersek sorunun cevabı;
- olarak hesaplanır.

Tam Küp İfadeler

Tam küp özdeşlikler şu şekilde özetlenebilir:

Tam küp ifadeler aşağıdaki şekilde de ifade edilebilir:

✍ Örnek Soru Tipi – 1

olduğuna göre, işleminin sonucu kaçtır?

🖋 Çözüm

Öncelikle, soruda verilen ifadeyi sadeleştirelim. ifadesini tam küp ifadeye benzetebilmek için sabit sayısını 2 ve 1 şeklinde ayıralım.
Daha sonra b yerine soruda verilen değer yerine konulursa;
- olarak hesaplanır.

İki Küp Farkı

İki Küp Toplamı

xⁿ±yⁿ Şeklindeki İfadelerin Çarpanlara Ayrılması

n pozitif tam sayılarda tanımlı olmak üzere;

n tek sayı olmak üzere;

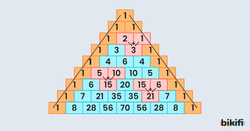
Pascal Üçgeni

x,y sayıları sıfır hariç reel sayılarda tanımlı ve n doğal sayı olmak üzere x + y nin kuvvetleri alınır ise aşağıdaki açılım elde edilir.

(x+y)⁰ = 1
(x+y)¹ = 1.x + 1.y
(x+y)² = 1.x² + 2.xy +1.y²
(x+y)³ = 1.x³ + 3.x²y + 3.xy² +1.y³
.
.
(x+y)ⁿ= .xⁿ y⁰+ . x^n-1 y +…+.x⁰yⁿ

Bu açılımdaki terimleri ortalayarak yazarsak şekilde görülen üçgen oluşur ve bu üçgene Pascal üçgeni denir.

📌 İpucu: Kare ve küp açılımlarının katsayılarını Pascal üçgeninden hesaplayabilirsiniz

Pascal üçgeninde herhangi ardışık iki sayı toplandığında bulunan değer sonraki alt satırdaki iki sayının ortasında yer alan sayıya eşit olur.

Değişken Değiştirme ile Çarpanlarına Ayırma Yöntemi

Karmaşık ifadeleri basitleştirmek için değişken değiştirme yöntemi kullanılır. Değişken değiştirme yöntemi ile çarpanlarına ayırma şu şekilde gerçekleştirilir.

Basitleştirilmek istenen karmaşık ifade seçilir.
Seçilen ifade x gibi basit bir değişkenle değiştirilir.
İfade çarpanlarına ayrılır.
Basit değişken silinerek yerine karmaşık ifade yazılır.
Elde edilen sonuç üzerinde sadeleştirme yapılabiliyorsa sadeleştirme işlemi yapılır.

✍ Örnek Soru Tipi – 1

ifadesinin en sade hali nedir?

🖋 Çözüm

Öncelikle olacak şekilde değişken değiştirelim.
Bulduğumuz sonuçta tersine dönüşümü uygulayalım.

ax²+bx+c Biçimindeki Üç Terimli İfadelerin Çarpanlara Ayrılması

ax²+bx+c şeklindeki ifadeleri çarpanlarına ayırabiliriz. Burada dikkat edilmesi gereken ilk nokta a katsayısının 1 olup olmadığıdır.

a Sayısı 1’e Eşitse

Bu durumda verilen denklemde toplamları b (b=m+n) ve çarpımları c (c=m.n) olan iki sayı (m ve n) bulunuyorsa bu ifadenin çarpanlarına ayrılmış şekli aşağıdaki gibi olur.

x²+bx+c
x²+(m+n)x+m.n
(x+m).(x+n)

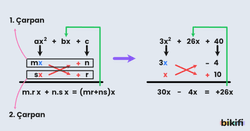
a Sayısı 1’e Eşit Değilse

Bu durumda a=m.s , c=n.r ve b=m.r+n.s olacak şekilde m,n,r ve s gerçek sayılar olmak üzere;

Terim Ekle Çıkar Yöntemi

Daha önce verilen yöntemlerle çarpanlarına ayrılamayan ifadelere, uygun terim ekleyip çıkararak, ifade bilinen özdeşliklere benzetilebilir.

✍ Örnek Soru Tipi – 1

ifadesinin en sade hali nedir?

🖋 Çözüm

Öncelikle olacak şekilde değişken değiştirelim.
Elde ettiğimiz ifadeyi ifadesine benzetebilmek için denkleme x eklenip çıkarılmalıdır.
Ardından, 1. adımda uyguladığımız dönüşümü tersine uygulayalım.
İki kare farkı formülünü uygularsak, soruda verilen ifadenin en sade halini bulmuş oluruz.

Çarpanlara Ayırma

Konu Özeti