Polinomlarda Dört İşlem

Sayılarda yaptığımız dört işlem gibi polinomlarda da dört işlem yapabiliriz. Polinomlarda toplama, çıkarma, çarpma ve bölme işlemleri yapılabilir.

❗❗ Uyarı: Sorularda polinom işlemleri yapılırken sadece polinomun derecesi hakkında yorum yapılması istenebilir. Böyle bir durumda polinomu sadece xⁿ şeklinde düşünerek istenen işlemi gerçekleştirebilirsiniz.

Polinomlarda Toplama ve Çıkarma İşlemi

Sayılardaki toplama işlemi gibi polinomlarda da toplama işlemi yapılır. Polinomların aynı dereceli terimleri kendi arasında toplanıp çıkarılabilir.

Polinomlarda toplama ve çıkarma işlemi sonucunda elde edilen polinomun derecesi, derecesi en büyük olan polinomun derecesine eşit olur.

Örnek

polinomları veriliyor.
P(x)+Q(x) ve 2.P(x)-3Q(x) işlemlerinin sonucunu bulunuz.

✍ Çözüm

Polinomlarda Çarpma İşlemi

Polinomlar çarpılırken birinci polinomun ilk terimi, ikinci polinomun her terimiyle ayrı ayrı çarpılır. Bu işlem birinci polinomun tüm terimleri için tekrar edilir. Terimlerin birbirleriyle çarpılması bittiğinde elde edilen benzer terimliler toplanır ve tek bir polinom cinsinden yazılır.

Örnek

Olduğuna göre, P(x).Q(x) i bulunuz.

✍ Çözüm

Dağılma özelliği kullanılarak çarpılır ise,
Düzenlemeler yapıldığında
bulunur.

Çarpma İşleminin Özellikleri

P(x) polinomunun derecesi b ve Q(x) polinomunun derecesi k olmak üzere,

P(x) * Q(x) işleminin derecesi = der[P(x) * Q(x)] = b+k olur.
P{Q(x)} işleminin derecesi = der[P{Q(x)}] = b*k olur.
işleminin derecesi = der[] = n*b olur.
işleminin derecesi = der[] = n*b olur.

🚀 Çarpma işleminin derece cinsinden hesaplanmasını kolaylaştırmak için derecesi b olan P(x) polinomu olarak düşünülebilir. Aynı şekilde derecesi k olan Q(x) polinomu için olarak düşünülebilir.

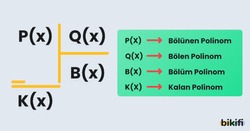
Polinomlarda Bölme İşlemi

P(x), Q(x) birer polinom, ve der[P(x)] der[Q(x)] olmak üzere; polinomları arası bölme işlemi şu şekilde gerçekleştirilir.

Bölme İşleminin Özellikleri

der[K(x)]<der[Q(x)]
K(x) = 0 ise P(x) polinomu Q(x) polinomuna tam bölünür.
P(x) polinomunun derecesi b, Q(x) polinomunun derecesi k olmak üzere;

Polinomlarda Bölme İşleminde Kalan Bulma

Yukarıdaki bölme işleminden yola çıktığımızda, P(x) = Q(x) * B(x) + K(x) olarak ifade edilir.

P(x) polinomunun Q(x) polinomuyla bölünmesinden kalan K(x) olacaktır.

Kalanı bulmak için Q(x) polinomunu ax+b şeklinde ifade edelim.
Böylece ax+b denkleminin kökü (yani bu ifadeyi sıfır yapan değer)
- Örneğimiz için kök değerimiz, olacaktır.
Bu durumda, P(x) = (ax+b) * B(x) + K(x) olacaktır.
Ardından Q(x) polinomunu sıfır yapan değer (2. adımda bulunan) P(x) polinomunda yerine yazılır.
Bölen polinomun kökleri bölünen polinomunda yerine yazıldığında bulunan değer kalanı verir.

Örnek

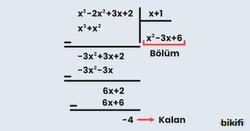
polinomunun x+1 ile bölümünden elde edilen bölümü bulunuz.

✍ Çözüm

Polinomun Q(x)’e Tam Bölünmesi

P(x) polinomu Q(x)’ tam bölünüyorsa bölme işleminin 2. özelliğinden dolayı K(x) polinomunun 0’a eşit olduğu bilinmektedir. Bu koşulu yukarıdaki son denklemde yerine koyduğumuzda

Sonucunu elde ederiz.

🚀 Yani Q(x) polinomuna tam olarak bölünen bir P(x) polinomuna, Q(x) polinomunun kökleri yazılırsa P(x) polinomu 0’a eşit olur.

Örnek

polinomu verilmiştir.

✍ Çözüm

P(x) in x-1 ile bölümünden kalan kaçtır?
- x-1=0 ise x=1 değeri P(x) polinomunda yerine yazılırsa kalan bulunur.
- P(x) in x-1 ile bölümünden kalan P(1)=1 olarak bulunur.
P(x+1) in x+3 ile bölümünden kalan kaçtır?
- x+3=0 ise x=-3 değeri bölünen P(x+1) polinomunda yerine yazılırsa kalan bulunur.
- P(-3+1) = P(-2) olur.
- P(x+1) in x+3 ile bölümünden kalan P(-2)=-29 olarak bulunur.
P(2x-1) in x-2 ile bölümünden kalan kaçtır?
- x-2=0 ise x=2 değeri P(2x-1) polinomunda yerine yazılırsa kalan bulunur.
- P(2.(2)-1) = P(3) olur.
- P(2x-1) in x-2 ile bölümünden kalan P(3)=-29 olarak bulunur.