Üçgenlerin Eşliği
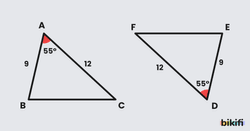
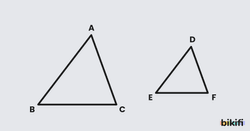
Bütün iç açıları ve kenar uzunlukları birbirine eşit olan üçgenlere eş üçgenler denir. Sorularda iki eş üçgen olduğu bilgisi verildiğinde bir üçgenin açılarına ve kenar uzunluklarına bakarak diğer üçgendeki aynı açının karşısına kenar uzunluğunu veya kenara bakarak karşısındaki açıyı yazabilirsiniz. Bu tür sorularda genelde üçgenler birbirine göre yansımış veya çevrilmiş olacaktır, bu yüzden görsel olarak benzetmekten çok açıları ve kenar uzunluklarını kıyaslamak kolaylık sağlayacak ve hız kazandıracaktır. Yine sorularda birazdan vereceğim benzerliklerle bir üçgenin bilgileri sayesinde başka üçgenin bilgilerini yazabileceğiz.
Ayrıca sorularda verilen eşitliklerinde harf sıralamasına bakılarak hangi harflerin birbirine karşılık geldiğini öğrenebiliriz. Örnek olarak bir eşitliğine baktığımızda A harfinin yerinde D, B harfinin yerinde E, C harfinin yerinde F harflerinin olduğunu hayal edebiliriz. Bu bilgilerden yola çıkarak;
|AB| = |DE| , |BC| = |EF| , |AC| = |DF| yorumlarını yapabiliriz.
Üçgenlerde Eşlik Kuralları
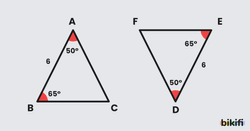
Aşağıdaki kurallarda söylenilen sırayla verilen açı ve kenar uzunluklarına göre tek bir üçgen oluşabileceği için iki üçgende aynı açı ve kenar uzunluklarını aynı sırayla gördüğümüzde bu üçgenlere eş üçgenler diyebiliriz.
Kenar-Açı-Kenar(K.A.K.) Eşlik Kuralı
İki üçgen arasında yapılan bire bir eşlemede karşılıklı ikişer kenar uzunlukları ve bu kenarlar arasında kalan açı ölçüleri eşit ise bu üçgenler eş üçgenler olur.
Açı-Kenar-Açı(A.K.A) Eşlik Kuralı
İki üçgen arasında yapılan bire bir eşlemede karşılıklı ikişer açının ölçüleri ve bu açılar arasında kalan kenar uzunlukları eşit ise bu üçgenler eş üçgenler olur.
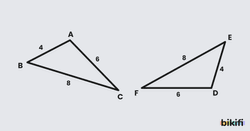
Kenar-Kenar-Kenar(K.K.K.) Eşlik Kuralı
İki üçgen arasında yapılan bire bir eşlemede karşılıklı bütün kenar uzunlukları eşit ise bu üçgenler eş üçgenlerdir. Bu durumda üçgenlerin karşılıklı açıları da eştir.
Üçgenlerin Benzerliği
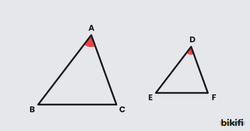
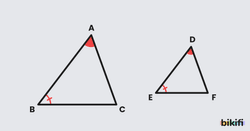
Bütün iç açıları eşit fakat kenar uzunlukları arasında belli bir oran olan üçgenlere benzer üçgenler denir. Benzerlik durumu “~” sembolü ile gösterilir. Benzer üçgenlerde birinin kenar uzunluğu diğer üçgende ona karşılık gelen kenarın iki katıysa diğer kenarlar için de aynı orantıyı yapabiliriz.
Örnek olarak benzerliğinde şu yorumları yapabiliyoruz;
- burada benzerlik sabitidir, herhangi bir sayı olabilir. ise bu üçgenler eştir.
Üçgenlerde Benzerlik Teoremleri
Aşağıdaki teoremlerde söylenilen sırayla verilen açı ve kenar uzunluklarına göre tek bir üçgen oluşabileceği için iki üçgende aynı açı ve birbiriyle orantılı kenar uzunluklarını aynı sırayla gördüğümüzde bu üçgenlere benzer üçgenler diyebiliriz.
Kenar-Açı-Kenar(K.A.K.) Benzerlik Teoremi
İki üçgenin karşılıklı ikişer kenarlarının uzunlukları orantılı ve bu orantılı kenarlar arasındaki açıları eş ise bu iki üçgen benzerdir. Bu benzerliğe Kenar-Açı-Kenar (K.A.K.) benzerliği denir.
Kenar-Kenar-Kenar(K.K.K.) Benzerlik Teoremi
İki üçgenin karşılıklı kenar uzunlukları orantılı ise bu iki üçgen benzerdir. Bu benzerliğe Kenar-Kenar-Kenar (K.K.K.) benzerliği denir.
Bu durumda :
Açı-Açı (A.A.) Benzerlik Teoremi
İki üçgen arasında yapılan bire bir eşlemede karşılıklı ikişer açısı eş ise üçgenler benzerdir. Bu benzerliğe Açı-Açı (A.A.) benzerliği denir. Bu üçgenlerde iki açısı eşit olduğunda üçüncü açı da eşit olacağından iki üçgende aynı açıların karşısındaki kenar uzunlukları arasında mutlaka bir orantı olacaktır.
Temel Orantı Teoremi
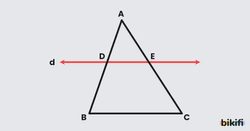
Bir üçgenin bir kenarına paralel olan ve diğer iki kenarını kesen bir doğru, kestiği kenarları orantılı olarak böler.
d // [BC] ise olur.
Benzer üçgenlerde kenar uzunlukları arasında olduğu gibi aynı köşeden indirilen dik, açıortay ve kenarortaylar arasında da aynı orantı bulunur.
Thales Teoremi
Thales Teoremi 1
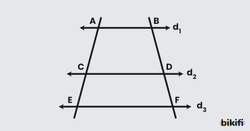
İki farklı doğru, en az üç paralel doğru ile kesildiğinde orantılı parçalara ayrılır.
d1 // d2 // d3 ise olur.
Thales Teoremi 2
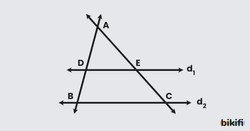
Kesişen iki doğrunun, paralel iki doğru tarafından kesilmesiyle oluşan üçgenlerin kenarları orantılıdır. Yani burada ABC ve ADE üçgenleri arasındaki benzerliği kullanarak kenarları arasında orantı kurabiliriz.
I. Thales Teoreminde üst köşelerden sağdaki veya soldaki doğruya paralel indirdiğimiz zaman II. Thales Teoremine dönüştürebiliriz.
Kelebek Benzerliği
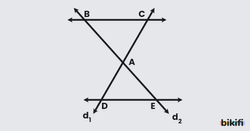
İki paralel doğru arasında çakışan başka iki doğru olduğunda iki benzer üçgen ortaya çıkar. Ters durmuş iki üçgen yan bakıldığında bir kelebeği andırdığı için bu isim verilmiştir. Yukarıdaki şekilde d1 doğrusu iki paralel doğruyu kestiği için ‘Z Kuralı‘ uygulayabiliriz. Bu durumda olacaktır. A noktasında yukarı ve aşağı bakan açılar ters açılardır ve birbirine eşittir. Bu veriler ışığında üçgenlerinin bütün iç açıları eşit olduğu için benzer üçgenlerdir. Bu benzerlikten yola çıkarak aşağıdaki yorumu yapabiliriz.