Üçgenin Yardımcı Elemanları: Açıortay

Açıortay

Bir açıyı iki eş açıya ayıran ışına açıortay denir. Açıortay iç ve dış açıortay olmak üzere ikiye ayrılır.

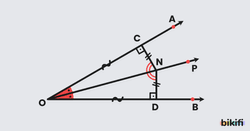
[OP ışını, açısının açıortayıdır.

Açıortay doğrusu üzerindeki herhangi bir noktanın açının kollarına olan uzaklıkları eşittir. Unutulmaması gereken bir kuraldır ve ispatı aşağıdaki gibidir.

Açıortay Teoreminin İspatı

Açıortay üzerindeki herhangi bir N noktasından açının kollarına dikmeler indirelim. Elde edilen üçgenlerinin tüm açıları eşit ve ortak bir kenarı olduğundan bu üçgenler eştir. Bu durumda aşağıdaki yorumları yapabiliriz.

|NC|=|ND|
|OC|=|OD|

Üçgende İç Açıortay

Bir üçgenin bir iç açısını iki eş açıya ayıran ışına o üçgenin iç açıortayı denir. Bir üçgende iç açıortaylar tek noktada kesişir. I noktası, iç açıortayların kesişim noktasıdır.

Bir üçgende iç açıortayların kesişim noktası üçgenin iç teğet çemberinin merkezidir. Sağdaki görsele göre

I noktası iç açıortayların kesişim noktası ve üçgenin iç teğet çemberinin merkezdir.
D, E, F noktaları çemberin üçgene teğet noktaları olmak üzere
|IE|=|ID|=|IF|=r iç teğet çemberin yarıçapıdır.
|AD|=|AE| , |BD|= |BF| , |CF|=|CE|

Üçgende İç Açıortay Teoremi

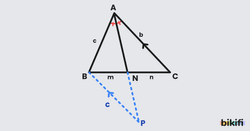
ABC üçgeninde;

A açısına ait açıortay doğrusunun [BC] kenarını kestiği nokta N olsun.
|AB|=c, |AC|=b , |BN|=m, |NC|=n olmak üzere
dir.

Üçgende İç Açıortay Teoreminin İspatı

B noktasından [AC] kenarına paralel çizilen doğru [AN]’yi P noktasında kesiyor.
İç ters açılardan üçgeni ikizkenar olur.
Dolayısıyla |AB| = |BP| = c dir.
Kelebek Benzerliği’nden
olarak bulunur.

Üçgende İç Açıortay Uzunluğu Bulma

ABC üçgeninde;

[AN] iç açıortay ve |AN|= x olsun.
|AB| = c, |AC| = b, |BN| = m, |NC| = n olmak üzere
dir.

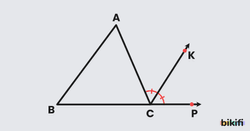
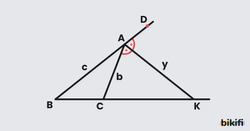
Üçgende Dış Açıortay

Bir üçgenin bir dış açısını iki eş açıya ayıran ışına o üçgenin dış açıortayı denir.

ABC üçgeninde dış açısının açıortayı olan [CK , C açısına ait dış açıortaydır.

Bir üçgende iki dış açıortay ile üçüncü açının iç açıortayı tek noktada kesişir. Bu nokta, üçgenin dış teğet çemberinin merkezidir. Bir üçgenin üç tane dış teğet çemberi vardır.

Yukarıdaki görselde gösterilen dış teğet çember A açısına aittir. Her iç açıya ait bir dış teğet çember bulunur ve bu çemberlerin yarıçapları farklıdır.

A, B ve C açılarına ait dış teğet çemberlerin merkezleri sırasıyla ile gösterilir.
D, E ve F noktaları çemberin değme noktaları olmak üzere
olup A açısına ait dış teğet çemberinin yarıçapı dır.
Benzer şekilde B açısına ait dış teğet çemberin yarıçapı , C açısına ait dış teğet çemberinin yarıçapı dir.

Üçgende Dış Açıortay Teoremi

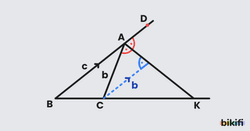
ABC üçgeninde;

[AK] dış açıortay, K ise dış açıortayın [BC ışınını kestiği nokta,
|AB| = c, |AC| = b olmak üzere
dir

Üçgende Dış Açıortay Teoreminin İspatı

C köşesinden [AB] kenarına paralel olacak şekilde çizilen doğru [AK] dış açıortayını L noktasında kesiyor.
üçgeni ikizkenar olur.
Bu durumda |AC| = |CL| = b dir.
Dolayısıyla olduğundan
olarak bulunur.