Periyodik Fonksiyonlar
şartıyla fonksiyonundaki eşitlik sağlanıyorsa fonksiyonuna periyodik fonksiyon, T gerçek sayısına ise fonksiyonun periyodu denir. Bu eşitlikte T sayılarından içinden en küçük pozitif sayıya fonksiyonun esas periyodu denir.
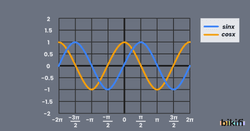
Daha iyi anlamak için örnek verecek olursak fonksiyonlarını inceleyelim. Her tam sayısı için 2π(360°) eklenecek veya çıkarılacağı için sinüs veya kosinüs fonksiyonlarının sonucunda bir değişiklik olmayacaktır. Bunun sonucunda aşağıda verilen grafiklerde görüldüğü gibi sürekli tekrar eden bir fonksiyona ulaşacağız. Sinüs ve kosinüs fonksiyonları için periyodik fonksiyon diyebiliriz ve periyodunu bulmak istersek T=k.2π eşitliğinde k=1 için periyodumuz T=2π olacaktır.
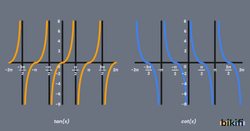
Yukarıdaki tanjant ve kotanjant fonksiyonlarından tanımsız yapan değerler çıkarıldığında iki fonksiyon için de her π(180°) eklendiğinde veya çıkarıldığında yine aynı sonucu vereceğini görüyoruz. Bu durumda tanjant ve kotanjant fonksiyonlarına T=k.π eşitliğinde k=1 için T=π periyoduna sahip birer periyodik fonksiyon diyebiliriz. Aşağıda tanjant ve kotanjant fonksiyonlarına ait
f(x)=p.sin(ax+b)+c veya g(x)=p.cos(ax+b)+c Fonksiyonlarının Periyotları
şartıyla f(x)=p.sin(ax+b)+c ve g(x)=p.cos(ax+b)+c fonksiyonlarının periyodik olup olmadığını anlamak için f(x)=f(x+T) eşitliğinde T periyodunu bulmamız gerekmektedir.
Bu durumda f(x)=p.sin(ax+b)+c ve g(x)=p.cos(ax+b)+c fonksiyonları periyodu olan periyodik bir fonksiyondur.
f(x)=p.tan(ax+b)+c veya g(x)=p.cot(ax+b)+c Fonksiyonlarının Periyotları
Yukarıda yaptığımız gibi yine periyodik fonksiyon denklemini kullanarak bu sefer tanjant ve kotanjantın periyodik fonksiyon olup olmadığını inceleyeceğiz.
şartıyla f(x)=p.tan(ax+b)+c ve g(x)=p.cot(ax+b)+c fonksiyonlarından birini f(x)=f(x+T) eşitliğine sokalım.
Bulduğumuz sonuca göre tanjant ve kotanjant fonksiyonları da birer periyodik fonksiyonlardır ve periyodu ‘dir.