kπ/2 ∓ α Şeklinde İfade Edilen Açılar
Bu konuda ifadesi 90° ve katlarını ifade etmek için kullanılır. Burada k ifadesi bir katsayı olup her bir arttığında açıya 90° eklenir. Örnek olarak;
Genellikle bu 4 ifade kullanılır. Açılar her 360° ‘de bir tekrar ettiği için k’nin daha yüksek olduğu değerlerde 360° ‘nin altına inecek kadar 2 çıkartırsak yine yukarıda verdiğimiz örneklerden birine ulaşacağız.
k nin Tek Tam Sayı Olması Hali
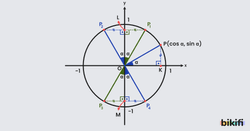
açısı yapan bir doğrunun birim çemberi kestiği noktanın x eksenini cos, y eksenini sin değerinde kestiğini öğrenmiştik. Şimdi ise bu yöntemden yola çıkarak ‘den çıkarılıp veya eklenen açıların diğer trigonometrik karşılıklarını aşağıdaki şekli kullanarak bulacağız.
Şekilde gördüğümüz noktalarını incelediğimizde bütün noktaların x ve y değerlerini başlangıca göre yaptığı açıların kosinüs ve sinüs değerleri sayesinde bulabiliriz.
Bu noktaların bir de y ekseniyle yaptığı açısına bağlı olarak bulabiliriz. Örnek olarak noktasını ele aldığımızda üçgeninin kenarı x eksenindeki değerini, OL kenarı y eksenindeki değerini verecektir. Üçgenin hipotenüs uzunluğu 1 olduğu için açısının karşısındaki kenar sinüs değerine, komşusundaki kenar kosinüs değerine eşit olacaktır. Sonuç olarak P noktasının x ve y değerleri aşağıdaki gibi olacaktır.
Yukarıdaki şekle geri döndüğümüzde bu 4 noktanın da eksenlere göre duruşları aynı olduğu için x ve y değerleri eşit fakat bulundukları bölgeye göre işaretleri farklı olacaktır.
Yukarıda 4 noktayı iki farklı şekilde bulduk. Bulduğumuz bu değerleri birbirine eşitleyerek belli bir açının trigonometrik fonksiyonu ile bu açıya ekleme veya çıkartma yapılmış halinin trigonometrik fonksiyonları arasındaki ilişkileri inceleyeceğiz.
P1 noktası : π/2-α (90-α)
Yukarıda noktasını hem başlangıca göre yaptığı açıya göre hem de y ekseniyle oluşturduğu üçgeninden bulduk. Bu değerleri eşitleyip trigonometrik fonksiyonlar arasındaki ilişkileri bulalım.
- x ekseni:
- y ekseni:
Bir açısının sinüs değeri, bu açıyı 90° ‘den çıkarttığımız zamanki kosinüs değerine eşit olur. Bu durum sinüs ve kosinüs yer değiştirmiş halde yine aynıdır. Aşağıda bununla ilgili birkaç örnek verelim.
Pratik bilgi olarak yukarıdaki eşitlikleri incelediğimizde birbirini 90° ‘ye tamamlayan açılardan birinin sinüs değeri diğer açının kosinüs değerlerine eşit olduğu sonucuna varırız.
Yukarıdaki tanjant ve kotanjant durumunu pekiştirmek için birkaç örnek inceleyelim.
Sinüs ve kosinüste olduğu gibi burada da birbirini 90° ‘ye tamamlayan açılardan birinin tanjant değeri diğer açının kotanjant değerlerine eşit olacaktır.
P2 noktası : π/2+α (90+α)
Yukarıda noktasını hem başlangıca göre yaptığı açıya göre hem de y ekseniyle oluşturduğu üçgeninden bulduk. Bu değerleri eşitleyip trigonometrik fonksiyonlar arasındaki ilişkileri bulalım.
- x ekseni:
- y ekseni:
Bir açısının sinüs değeri, bu açıya 90° eklediğimiz zamanki kosinüs değerinin eksi işaretlisine eşit olur fakat aynı durum kosinüste açısı bulunduğunda sinüsün işareti aynı olur. Bu durumu koordinat düzlemi üzerinde düşünelim. olarak aldığımız zaman sin30 değeri artı işaretken cos120 negatif işaretlidir. olarak alırsak değeri negatif işaretken değeri pozitif işaretlidir. Sonuç olarak ‘ya geçerken hep birbirlerinin zıt işaretlisi olacağından negatif işaretine eşittir. durumu için incelersek kosinüs değerinin pozitif işaretli olduğu yerlerde sinüsün de pozitif, kosinüsün negatif işaretli olduğu yerlerde sinüsün de negatif olduğunu görürüz. Bu yüzden eşitlikte herhangi bir negatif işaret durumu olmaz. Aşağıda bu durumu pekiştirmek ve üzerine düşünmek adına birkaç örnek bulunmaktadır.
Pratik bilgi olarak sinüs ve kosinüs fonksiyonlarından birinin açısının diğerinin açısından 90° fazla olduğunu gördüğümüzde birbirine eşit ve büyük açılı olan kosinüs ise zıt işaretli, sinüs ise aynı işaretlidir.
Yukarıdaki tanjant ve kotanjant durumunu pekiştirmek için birkaç örnek inceleyelim.
Tanjant ve kotanjant fonksiyonlarında birinin açısının diğerinin açısından 90° fazla olduğunu gördüğümüz zaman birbirine eşit ve zıt işaretli yorumunu yapabiliriz.
P3 noktası : 3π/2-α (270-α)
Yukarıda noktasını hem başlangıca göre yaptığı açıya göre hem de y ekseniyle oluşturduğu üçgeninden bulduk. Bu değerleri eşitleyip trigonometrik fonksiyonlar arasındaki ilişkileri bulalım.
- x ekseni:
- y ekseni:
Bir açısının sinüs değeri, bu açıyı 270° ‘den çıkarttığımız zamanki kosinüs değerinin negatifine eşit olur. Bu durum sinüs ve kosinüs yer değiştirmiş halde yine aynıdır. Aşağıda bununla ilgili birkaç örnek verelim.
Pratik bilgi olarak yukarıdaki eşitlikleri incelediğimizde birbirini 270° ‘ye tamamlayan açılardan birinin sinüs değeri diğer açının kosinüs değerlerine eşit fakat zıt işaretli oldukları sonucuna varırız.
Yukarıdaki tanjant ve kotanjant durumunu pekiştirmek için birkaç örnek inceleyelim.
Tanjant ve kotanjantta da birbirini 270° ‘ye tamamlayan açılardan birinin tanjant değeri diğer açının kotanjant değerlerine eşittir.
P4 noktası : 3π/2+α (270+α)
Yukarıda noktasını hem başlangıca göre yaptığı açıya göre hem de y ekseniyle oluşturduğu üçgeninden bulduk. Bu değerleri eşitleyip trigonometrik fonksiyonlar arasındaki ilişkileri bulalım.
- x ekseni:
- y ekseni:
Bir açısının kosinüs değeri, bu açıya 270° eklediğimiz zamanki sinüs değerinin eksi işaretlisine eşit olur fakat aynı durum sinüste açısı bulunduğunda kosinüsün işareti aynı olur. Bu durumu koordinat düzlemi üzerinde düşünelim. =30° olarak aldığımız zaman değeri artı işaretken negatif işaretlidir. olarak alırsak değeri negatif işaretken değeri pozitif işaretlidir. Sonuç olarak dan ya geçerken hep birbirlerinin zıt işaretlisi olacağından negatif işaretine eşittir. durumu için incelersek sinüs değerinin pozitif işaretli olduğu yerlerde kosinüsün de pozitif, sinüsün negatif işaretli olduğu yerlerde kosinüsün de negatif olduğunu görürüz. Bu yüzden eşitlikte herhangi bir negatif işaret durumu olmaz. Aşağıda bu durumu pekiştirmek ve üzerine düşünmek adına birkaç örnek bulunmaktadır.
Normalde pratik bilgi olarak sinüs ve kosinüs fonksiyonlarından birinin açısının diğerinin açısından 270° fazla olduğunu gördüğümüzde birbirine eşit ve büyük açılı olan sinüs ise zıt işaretli, kosinüs ise aynı işaretlidir diyebiliriz fakat yukarıdaki örneklere baktığımızda açısı 360° ‘yi geçen fonksiyonların açılarını tekrar yazdığımızda aralarındaki farkın 270° değil 90° olduğunu görürüz. Bu durumda aslında noktasında anlattıklarımız devreye giriyor.
Yukarıdaki tanjant ve kotanjant durumunu pekiştirmek için birkaç örnek inceleyelim.
Tanjant ve kotanjant fonksiyonlarında birinin açısının diğerinin açısından 270° fazla olduğunu gördüğümüz zaman birbirine eşit ve zıt işaretli yorumunu yapabiliriz fakat 360° ‘yi aşan açıları düzenlediğimizde aralarında 90° fark oluyor ama değişen bir şey olmuyor tabi.
k nin Çift Tam Sayı Olması Hali
Bu bölümde trigonometrik fonksiyonlar arasındaki eşitliklerden bu fonksiyonların kendi içlerindeki açı ve işaret değişikliklerine değinmiş olacağız.
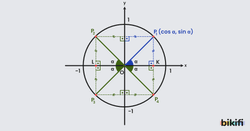
açısı yapan bir doğrunun birim çemberi kestiği noktanın x eksenini , y eksenini değerinde kestiğini öğrenmiştik. Şimdi ise bu yöntemden yola çıkarak ‘den çıkarılıp veya eklenen açıların diğer trigonometrik karşılıklarını aşağıdaki şekli kullanarak bulacağız.
Şekilde gördüğümüz noktalarını incelediğimizde bütün noktaların x ve y değerlerini başlangıca göre yaptığı açıların kosinüs ve sinüs değerleri sayesinde bulabiliriz.
Bu noktaların bir de x ekseniyle yaptığı açısına bağlı olarak bulabiliriz. Örnek olarak noktasını ele aldığımızda üçgeninin OL kenarı x eksenindeki değerini, kenarı y eksenindeki değerini verecektir. Üçgenin hipotenüs uzunluğu 1 olduğu için açısının karşısındaki kenar sinüs değerine, komşusundaki kenar kosinüs değerine eşit olacaktır. Sonuç olarak noktasının x ve y değerleri aşağıdaki gibi olacaktır.
Yukarıdaki şekle geri döndüğümüzde bu 4 noktanın da eksenlere göre duruşları aynı olduğu için x ve y değerleri eşit fakat bulundukları bölgeye göre işaretleri farklı olacaktır.
Artık noktaları iki farklı şekilde bulduğumuza göre aynı noktalar için bulduğumuz değerleri birbirine eşitleyerek trigonometrik fonksiyonların kendi içindeki açı değişikliklerini inceleyeceğiz.
P2 noktası : π-α (180-α)
Yukarıda noktasını hem başlangıca göre yaptığı açıya göre hem de x ekseniyle oluşturduğu üçgeninden bulduk. Bu değerleri eşitleyip trigonometrik fonksiyonların kendi arasındaki ilişkileri bulalım.
- x ekseni:
- y ekseni:
Bir açısının ve 180° ‘den çıkartılmış halinin kosinüs değerleri birbirine eşit fakat zıt işaretli, sinüs değerleri ise birbirine eşit ve işaretleri aynıdır. Aşağıda bu durumla ilgili örnekler verilmiştir.
Koordinat düzleminde bu örnekleri incelediğimizde bir açıyı 180° den çıkarttığımız zaman aslında y eksenine göre simetriğini almış gibi oluruz. Bu durumda sinüs hep aynı değerde kalırken kosinüs büyüklük olarak aynı fakat işareti hep tersi olur.
Toplamları 180° olan açıların tanjant veya kotanjant değerleri birbirine eşit fakat kosinüsteki işaret değişimden dolayı zıt işaretlidir.
P3 noktası : π+α (180+α)
Yukarıda noktasını hem başlangıca göre yaptığı açıya göre hem de x ekseniyle oluşturduğu üçgeninden bulduk. Bu değerleri eşitleyip trigonometrik fonksiyonların kendi arasındaki ilişkileri bulalım.
- x ekseni:
- y ekseni:
Bir açısının ve 180° ‘den çıkartılmış halinin kosinüs ve sinüs değerleri birbirine eşit fakat zıt işaretlidir. Aşağıda bu durumla ilgili örnekler verilmiştir.
Koordinat düzleminde bu örnekleri incelediğimizde bir açıya 180° eklediğimiz zaman aslında O noktası yani koordinat düzleminin merkezine göre simetriğini almış gibi oluruz. Bu durumda x ve y değerlerinin büyüklükleri eşit fakat ikisi de işaret değiştirir. Bundan dolayı sinüs ve kosinüs fonksiyonlarının da işaretleri değişir.
Aralarında 180° fark olan tanjant veya kotanjant değerleri birbirine eşittir. Hem sinüs hem de kosinüs aynı anda işaret değiştirdikleri için tanjant ve kotanjant fonksiyonlarının işaretleri aynı kalır.
P4 noktası : 2π-α (360-α)
Yukarıda noktasını hem başlangıca göre yaptığı açıya göre hem de x ekseniyle oluşturduğu üçgeninden bulduk. Bu değerleri eşitleyip trigonometrik fonksiyonların kendi arasındaki ilişkileri bulalım.
- x ekseni:
- y ekseni:
Bir açısının ve 360° ‘den çıkartılmış halinin sinüs değerleri birbirine eşit fakat zıt işaretli, kosinüs değerleri ise birbirine eşit ve işaretleri aynıdır. Aşağıda bu durumla ilgili örnekler verilmiştir.
Koordinat düzleminde bu örnekleri incelediğimizde bir açıyı 360° den çıkarttığımız zaman aslında x eksenine göre simetriğini almış gibi oluruz. Bu durumda kosinüs hep aynı değerde kalırken sinüs büyüklük olarak aynı fakat işareti hep tersi olur.
Toplamları 360° olan açıların tanjant veya kotanjant değerleri birbirine eşit fakat sinüsteki işaret değişimden dolayı zıt işaretlidir.
P1 noktası : 2π+α (360+α)
Yukarıda noktasını hem başlangıca göre yaptığı açıya göre hem de x ekseniyle oluşturduğu üçgeninden bulduk. Bu değerleri eşitleyip trigonometrik fonksiyonların kendi arasındaki ilişkileri bulalım.
- x ekseni:
- y ekseni:
Hepimizin bildiği gibi koordinat düzleminde açılar her 360° ‘de bir tekrar eder. Yani bir açıya 360° eklemek veya çıkartmak sinüs ve kosinüs değerlerinde bir etki yapmayacaktır. Sinüs ve kosinüste bir değişim olmayınca tanjant ve kotanjant değerleri de aynı kalır. Aşağıdaki birkaç örnekle konumuzu bitirelim.