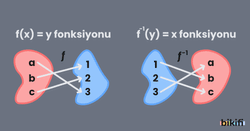
Bir fonksiyonun tersinin de fonksiyon olabilmesinin şartı bu fonksiyonun birebir ve örten olması gerekir çünkü fonksiyon tersine döndüğünde yine ilk hali gibi her girdiye ait bir çıktının olması gereklidir. Trigonometrik fonksiyonlar bütün reel sayı aralıklarında birebir ve örten değildir. Bu yüzden x ve y değerleri için belirli aralıklar belirlemeliyiz ki birebir ve örten durumunda olup tersi de fonksiyon olabilir.
Sinüs Fonksiyonunun Ters Fonksiyonu
Arcsin Tanım Aralığının Bulunması
Sinüs fonksiyonunda x yerine ne yazarsak yazalım y her zaman [-1,1] aralığında olacaktır. Bu aralığı veren x değerlerinden sadece bir tanesine sahip olmalıyız ki fonksiyonumuz birebir ve örten olabilsin. Sinüs fonksiyonu için …,,,,,,… aralıkları hepsi tek tek alındığında birebir ve örten olmaktadır. Bu aralıklardan en çok kullandığımız aralığını ele alalım.
fonksiyonu artık birebir ve örten olduğu için tersi de vardır.
Arcsin Fonksiyonu
fonksiyonu sinüs fonksiyonunun ters fonksiyonudur. Bu ters fonksiyonu şeklinde gösterebiliriz.
Aşağıda kıyaslama yaparak daha iyi anlaşılması için sinüs fonksiyonunun birebir ve örten durumda olduğu aralıkta kendisi ve tersi için bazı değerler ve karşılıkları tablo şeklinde yazılmıştır.
Arcsin’in Belirli Açılardaki Değerleri
| x | 0 | ||||
|---|---|---|---|---|---|
| y=sinx | -1 | 0 | 1 |
| x | -1 | 0 | 1 | ||
|---|---|---|---|---|---|
| y=arcsinx | 0 |
Örnekler
Aşağıdaki örneklerde sinüs fonksiyonlarının yanında ters fonksiyonları da yazılmıştır. Bir aralık belirtilmediğinde ters fonksiyonların birden fazla cevabı olabilir. Aşağıda ters fonksiyonlarının bazı olası sonuçları verilmiştir. Sorularda mutlaka bir aralık verilecektir ve o aralığa göre sonuçlardan sadece birisi doğru olacaktır.
Kosinüs Fonksiyonunun Ters Fonksiyonu
Arccos Tanım Aralığının Bulunması
Kosinüs fonksiyonu da aynı sinüs fonksiyonu gibi sonucu her zaman [-1,1] aralığındadır fakat farklı aralıklardaki x değerlerinde birebir ve örten olmaktadır. Kosinüs fonksiyonu [0,π] aralığında ve buna π kadar eklenip çıkartılan aralıklarda birebir ve örten olur. Biz genellikle kosinüs fonksiyonu için [0,π] aralığını kullanırız.
Arccos Fonksiyonu
fonksiyonu artık birebir ve örten olduğu için tersi de vardır.
fonksiyonu kosinüs fonksiyonunun ters fonksiyonudur. Bu ters fonksiyonu şeklinde gösterebiliriz.
Aşağıda kosinüs fonksiyonuna ve tersine ait bazı değerler ve karşılıkları tablolarda gösterilmiştir.
Arccos’un Belirli Açılardaki Değerleri
| x | 0 | ||||
|---|---|---|---|---|---|
| y=cosx | 1 | 0 | -1 |
| x | -1 | 0 | 1 | ||
|---|---|---|---|---|---|
| y=arccosx | 0 |
Örnekler
Aşağıda bazı kosinüs fonksiyonlarının sonuçları ve bunların ters fonksiyonlarının bazı olası sonuçları yazılmıştır. Sorularda verilen aralığa göre bu sonuçlar arasından doğru olanı seçeriz.
Tanjant Fonksiyonunun Ters Fonksiyonu
Arctan Tanım Aralığının Bulunması
Tanjant fonksiyonunun periyodu T=π olduğu için giriş değişkenlerinde her π aralığında bir aynı sonucu verir. Bu nedenle aralığını giriş değişkeni olarak tanımlarsak fonksiyon birebir ve örten olur.
Arctan Fonksiyonu
fonksiyonu birebir ve örten olduğu için artık tersi de vardır.
fonksiyonu tanjant fonksiyonunun ters fonksiyonudur. Bu ters fonksiyonu şeklinde gösterebiliriz.
Örnekler
Aşağıda tanjant fonksiyonunun bazı değerleri ve sonuçları yazılmıştır. Yanlarına ise bu fonksiyonların tersleri yazılarak olası bazı sonuçları yazılmıştır. Birden fazla cevabı olan bu ters fonksiyonların doğru cevabı sorularda verilen aralığa göre değişmektedir.