Sinüs Teoremi Formülü
Aşağıda kenar uzunlukları ; iç açıları ve çevrel çemberinin yarıçapı r olan bir ABC üçgeni vardır. Bu üçgen üzerinden sinüs teoremini uygulayalım.
Yukarıdaki formül incelendiğinde üçgenin bir kenar uzunluğu, karşısında bulunan açının sinüs değerine bölündüğünde bir katsayı elde edilir. Bulunan bu katsayı hem bütün kenarlara aynı işlemi uyguladığımızda çıkan sonuca hem de bu üçgenin çevrel çemberinin çapına eşit olacaktır.
Sinüs Teoremi İspatı
Formülü ezberlediğimize göre şimdi sırada nereden bulduğumuzu öğrenmek var. Sinüs Teoremini çevrel çember ve sinüslü alan formülünden bulabiliriz.
Çevrel Çember Yöntemi İle İspat
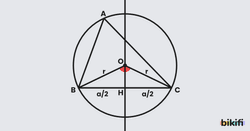
Aşağıda ABC üçgeni ve bu üçgenin merkezi O noktası ve yarıçapı r olan çevrel çemberi birlikte verilmiştir.
- OB ve OC yarıçaplarını çizdiğimiz zaman oluşacak olan merkez açısı, çevrel çemberde aynı yayı gören çevre açısının iki katı olacağından bağıntısını kurabiliriz.
- BOC üçgeni ikizkenar üçgen olduğu için O noktasından a kenarına indirilen yükseklik hem açısını hem de a kenarını iki eşit parçaya bölecektir. Bu bilgiler sonucunda açısı açısına eşit olacaktır.
- BOH üçgenine baktığımızda açısının sinüsünü bulmak istersek sonucuna varırız.
Yukarıda bulduğumuz bağıntıyı düzenlersek;
Bütün kenarlara uygulanırsa yine bu bağıntıya ulaşılır.
Sinüslü Alan Formülü Yöntemi İle İspat
Öncelikle bir ABC üçgeni için sinüslü alan formülünü vermek gerekirse;
bağıntısını yazarız.
- Formülde paydalarda bulunan bütün 2’leri sadeleştirip hepsini ‘ye bölelim.
- Bu aşamadan sonra sadeleştirmeleri yapalım.
- Pay ve paydaları yer değiştirirsek sinüs teoremi formülüne ulaşırız.
NOT: Bu yöntemde eşitliğin ‘ye eşit olduğunu bulamıyoruz.
Sinüs Teoremi Örnekleri
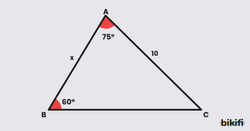
Örnek 1
Şekildeki ABC üçgeninde; olduğuna göre, değerinin kaç cm olduğunu bulunuz.
Çözüm
- Üçgenin iç açılarının toplamı 180° olduğu için bilinen iki açıyı toplayıp 180’den çıkartırsak üçüncü açıyı elde ederiz.
- Sinüs Teoremi formülünden;
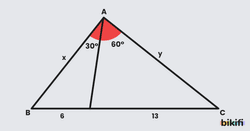
Örnek 2
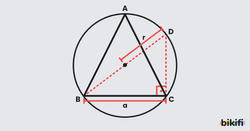
Şekildeki ABC üçgeninde olduğuna göre oranını bulunuz.
Çözüm
- diyelim.
- O zaman olur.
- Şekildeki ABD ve ADC üçgenlerine ayrı ayrı sinüs teoremi uygularız.
- Burada değerini iki farklı denklemde buluruz.
- Bulduğumuz bu değerleri birbirine eşitlersek aradığımız orantı çıkacaktır.
- ABD üçgeni :
- ADC üçgeni:
- Burada değerlerini bulduk artık eşitleyebiliriz.