Sayma ve Olasılık

Sayma Yöntemleri

Bir kümenin elemanları ile pozitif tam sayılar kümesinin ( ={1, 2,3, …}) elemanları arasında bire bir eşleme yaparak verilen kümenin elaman sayısını bulma işlemine bire bir eşleme yoluyla sayma denir. Kümenin son elemanı ile eşleşen doğal sayı kümesinin eleman sayısı olur.

Örnek: BİKİFİ kelimesinin harflerinden oluşan küme A={B,İ,K,İ,F,İ}, ={1, 2, 3, …} kümesinin elemanları ile bire bir eşlenirse s(A)= 6 bulunur.

A ve B şeklinde sonlu, ayrık iki küme olduğunu varsayalım. Bu kümelerin birleşim kümesinin eleman sayısını bulma işlemine toplama yoluyla sayma denir. Ayrık kümelerin birleşim kümesinin eleman sayısı s(A B)=s(A) + s(B) ile hesaplanır.

Örnek: 5 çeşit sıcak ve 6 çeşit soğuk içeceğin bulunduğu bir restoranda bir müşterinin sıcak veya soğuk içeceklerden birini kaç farklı şekilde seçebileceğini hesaplamak için toplama yoluyla sayma uygulanır. Çünkü bu iki küme ayrık kümelerdir ve yukardaki şartlara uygundur. Müşteri 5+6=11 farklı şekilde seçim yapabilir.

A ve B boş kümeden farklı, ayrık iki küme olmak üzere A x B kümesinde oluşan sıralı ikililerin eleman sayısını bulma işlemine çarpma yoluyla sayma veya saymanın temel ilkesi denir. s(A x B) = s(A).s(B) şeklinde hesaplanır.

• Bir A olayı ayrık A₁, A₂, …, A_r aşamalarında sırasıyla gerçekleşiyor olsun.
  • A₁ aşaması n₁ farklı yolla,
  • A₂ aşaması n₂ farklı yolla,
• A_r aşaması n_r farklı yolla gerçekleşmesi durumunda A olayı n₁ . n₂ … n_r farklı yolla gerçekleşir. s(A) = s(A₁ x A₂ x … x A_r) = n₁. n₂. …. .n_r dir.

Örnek: Bir restoranda 2 çeşit yemek ve 3 çeşit içecek vardır. Bir müşteri bir içecek ve bir yemek seçme koşuluyla kaç farklı seçim yapabilir. Y={y₁, y₂} yemekleri ve X={x₁, x₂, x₃} içecekleri bulunsun. Seçim sayısı Y x X={(y₁,x₁),(y₁,x₂),(y₁,x₃),(y₂,x₁),(y₂,x₂),(y₂,x₃)} elemanları kadardır. O halde s(Y x X) = s(Y) . s(X) = 2×3=6 farklı seçim yapılabilir.

Faktöriyel Kavramı

n bir pozitif tam sayı olmak üzere 1 den n ye kadar olan doğal sayıların çarpımına n faktöriyel denir ve n! şeklinde gösterilir.

• n!=1.2.3……(n-1).(n) dir.
  • 0!=1 kabul edilir.
  • 1!=1
  • 2!=1.2=2
  • 3!=1.2.3=6
  • 4!=1.2.3.4=24 şeklinde hesaplanabilir.
  • n!=n.(n-1)!=n.(n-1).(n-2)! şeklinde de yazılabilir.

Permütasyon (Sıralama)

r ve n pozitif tamsayılar olmak üzere, sonlu n elemanlı bir A kümesinin birbirinden farklı r (rn) elemanının her bir sıralanışına (dizilişine) A kümesinin r’li bir permütasyonu denir.

n elemanlı bir kümenin r’li tüm permütasyonlarının sayısı P(n,r) biçiminde gösterilir.

P(n,r)= n.(n-1).(n-2). …. (n-r+1)= dir.

n=r olması durumunda, n pozitif tamsayı olmak üzere, A kümesinin elemanlarının birbirinden farklı her sıralanışına A kümesinin permütasyonu denir. P(n,n)= olur.

Örnek:10 arkadaşın herhangi üçünün yan yana kaç farklı şekilde oturabileceği P(10,3)=10.9.8=720 şeklinde hesaplanabilir. 10 arkadaşın tamamının yan yana kaç farklı şekilde oturabileceği P(10,10)=10! şeklinde hesaplanmış olur.

Tekrarlı Permütasyon

Bazı elemanları özdeş olan n elemanlı bir kümenin n’li permütasyonuna tekrarlı permüstasyon denir. n elemanlı kümenin r₁ tanesi birinci türden r₂ tanesi ikinci türden, r₃ tanesi üçüncü türden, … ,r_k tanesi k ninci türden olmak üzere toplam n tane elemanının birbirinden farklı sıralanışlarının sayısı aşağıdaki formüldeki gibi bulunur.

Örnek: BİKİFİ kelimesindeki harfler ile anlamlı veya anlamsız 6 harfli kaç değişik kelime yazılabileceğini ve kaçının “İ” harfi ile başladığını hesaplayalım. 3 tane “İ”, 1 tane”B”, 1 tane “K”, 1 tane “F” harfi vardır. Yukarıda yazdığımız formüle göre kelime sayısı şeklinde bulunur. “İ” ile başlayanlar için ilk harf yazılır ve geriye kalan 2 “İ” ve diğerleri ile aynı işlem tekrarlanır. Yani

Dönel Permütasyon

n tam sayı olmak üzere n tane farklı elemanın dairesel permütastonlarının sayısına n elemanın dönel (dairesel) permütasyonu denir. n tane farklı elemanın dairesel dizilişlerinin sayısı (n-1)! tanedir.

Örnek: 7 öğrencilik bir grubun yuvarlak bir masa etrafında kaç farklı şekilde oturabileceği (7-1)!=6!=720 şeklinde hesaplanır.

Kombinasyon

n elemanlı kümenin r elemanlı alt kümelerinin sayısına n nin r li kombinasyonu denir. Kombinasyonda seçilen elemanların seçim sırası önemli değildir. Kombinasyonda sadece seçme işlemi vardır. Permütasyonda ise önce seçme, sonra da sıralama işlemi vardır.

n elemanlı bir kümenin r li kombinasyonlarının sayısı C(n,r)= şeklinde gösterilir.

Örnek: 7 elemanlı bir kümenin 3 elemanlı alt kümelerinin sayısı, şeklindedir.

Örnek: 5 doktor ve 4 hemşire arasından 3 doktor ve 2 hemşire ile 5 kişilik bir ekip kaç farklı şekilde oluşturulabilir? Bunu hesaplamak için öncelikle 5 doktorsan 3 ünü seçeriz daha sonra 4 hemşireden 2 sini seçeriz daha sonra saymanın çarpma ilkesinden 5 kişilik sağlık ekibi . şeklinde seçilir. Sonuç 60 olarak bulunur.

Bir düzlemde doğrusal olmayan noktalar verildiğinde

• İki noktadan bir doğru geçer yani n noktanın herhangi üçü doğrusal değil ise kaç doğru oluşturabileceği şeklinde hesaplanır.
• olmak üzere herhangi üçü doğrusal olmayan n tane nokta ile tane üçgen, tane dörtgen veya tane r kenarlı çokgen çizilebilir.

Örnek: Düzlemde bulunan 10 doğrunun en çok kaç noktada kesişebileceğini hesaplayalım. Doğrular birbirinden farklı olduğu için ya 1 noktada kesişirler ya da paraleldirler. En çok kesişme için herhangi ikisi paralel olmamalıdır. !0 doğrudan seçilen herhangi iki doğru 1 noktada kesişebileceğine göre oluşabilecek en çok nokta sayısı =45 olur.

Örnek: Bir daire üzerinde bulunan 15 farklı noktada köşeleri olacak şekilde kaç farklı üçgen çizilebilir? Çemberde yer alan noktalar doğrusal olmadığına göre herhangi üç nokta ile üçgen oluşturulabilir. şeklinde hesaplanır.

Pascal Üçgeni

x,y sayıları sıfır hariç reel sayılar ve n doğal sayı olmak üzere x + y nin kuvvetleri alınır ise aşağıdaki açılım elde edilir.

• (x+y)⁰ = 1
• (x+y)¹ = 1.x + 1.y
• (x+y)² = 1.x² + 2.xy +1.y²
• (x+y)³ = 1.x³ + 3.x²y + 3.xy² +1.y³
• .
• .
• (x+y)ⁿ = .xⁿ y⁰+ . x^n-1 y +…+.x⁰y⁰

Bu açılımdaki terimleri ortalayarak yazarsak şekilde görülen üçgen oluşur ve bu üçgene Pascal üçgeni denir.

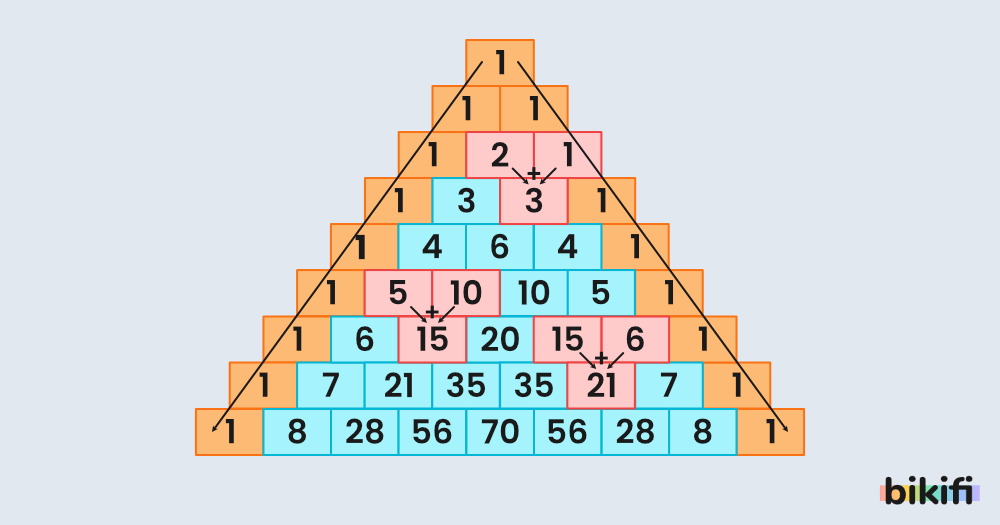
Pascal üçgeninde herhangi ardışık iki sayı toplandığında bulunan değer sonraki alt satırdaki iki sayının ortasında yer alan sayıya eşit olur.

Binom Açılımı

Binom teoremi

n N ve x ve y den en az biri sıfırdan farklı olmak üzere,

• (x+y)ⁿ = xⁿ y⁰+ x^n-1 y¹ + . x^n-2 y² +…..+.x⁰ yⁿ ‘dir.
• Binom teoremindeki katsayılar () Pascal üçgenin (n+1). satırındaki katsayılardır.

1. (x+y)ⁿ ifadesinin açılımda n+1 terim vardır.
2. (x+y)ⁿ ifadesinin açılımında her terimin x ve y nin üsleri toplamı n dir.
3. (x+y)ⁿ ifadesinin açılımda x ve y yerine (değişkenler yerine) 1 yazılırsa açılımdaki katsayılar toplamı, (1+1)ⁿ = 2ⁿ olarak bulunur.
4. (x+y)ⁿ ifadesinin açılımındaki sabit terim x=0 ve y=0 alınarak bulunur.
5. (x+y)²ⁿ açılımında ortadaki terim dir.
6. olduğundan, (x+y)ⁿ açılımında baştan ve sondan eşit uzaklıktaki terimlerin katsayıları mutlak değerce birbirine eşittir.
7. (x+y)ⁿ ifadesinin açılımında baştan (r+1) inci terim x^n-r y^r , sondan p ninci terim dir.