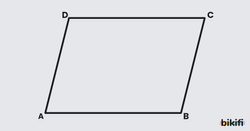
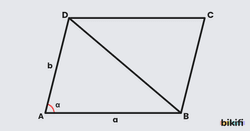
Karşılıklı kenarları birbirine paralel olan dörtgene paralelkenar denir.
Öncelikle paralelkenar, yamuğun tüm özelliklerine sahiptir. Bu özellikleri incelemek için bir önceki konumuz olan yamuk konusunu inceleyebilirsiniz.
Paralelkenarın en temel 3 özelliğinden bahsedecek olursak;
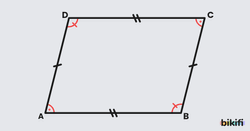
- Karşılıklı kenar uzunlukları birbirine eşittir.
- Karşılıklı duran açılar birbirine eşittir.
- Ardışık duran açıların toplamı 180° eder.
Paralelkenarda Açı ve Kenar Bağıntıları
Özellik 1
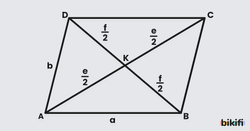
Paralelkenarda köşegenler birbirini ortalar ve her ikisi de iki eşit parçaya bölünür.
için;
Özellik 2
Paralelkenarda ardışık iki açının açıortayları birbirine dik uzanır.
İspat
Paralelkenarda ardışık iki açının toplamının 180° olduğunu söylemiştik. Her iki açının yarısını alırsak toplamda 90° eder. Açıortaylar birleştiğinde oluşan üçgende iki açının toplamı 90° ise kesiştikleri noktadaki açı da her zaman 90° olur. Bu özellik her kenar için kullanılabilir.
Özellik 3
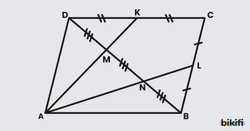
Aşağıdaki ABCD paralelkenarında |DB| köşegen A, K, L, M ve B, C, M noktaları doğrusaldır.
Bu durumda olur.
İspat
Yukarıdaki görselde 2 farklı renkte kelebek şekillerini görmekteyiz. Burada iki farklı kelebek benzerliği uygulayarak uzunluklar arasındaki ilişkileri kıyaslayarak ortak bir eşitlik çıkartabiliriz.
kelebek benzerliğinde aşağıdaki benzerliklere ulaşırız.
kelebek benzerliğinde ise aşağıdaki benzerliklere ulaşırız.
Bulduğumuz bu eşitliklerde ortak olarak ifadesini görüyoruz. Bu nedenle yukarıdaki bütün orantılar aslında birbirine eşittir. Bunlardan orantılarını alırsak;
içler dışlar çarpımı sonucunda ana formüle ulaşacağız.
Özellik 4
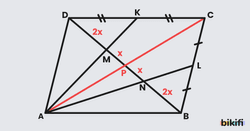
Paralelkenarda bir köşeden karşıdaki iki kenarın ortasına çekilen kenarortaylar yanındaki köşelerden çizilen köşegeni 3 eşit parçaya ayırır.
İspat
Kenarortaylar ve köşegen çizildiğinde kelebek benzerliği ortaya çıkar.
Öncelikle DB köşegeninin uzunluğunu 6x alalım.
kelebek benzerliğini kullanalım.
Buradan |MB| uzunluğunun |MD|’nin 2 katı olduğuna ulaşıyoruz. Köşegenin toplam uzunluğuna 6x dediğimize göre;
Aynı kelebek benzerliğini üçgenleri arasında kurarsak;
Bu seferde |DN| uzunluğunun |NB|’nin 2 katı olduğuna ulaşıyoruz.
DB köşegeninin DM ve NB aralıkları 2x uzunluğuna eşit olduğuna göre bu uzunlukları 6x’ten çıkartırsak geriye kalan MN uzunluğu da 2x olur.
Özellik 5
Bir paralelkenarda 2 köşegenin kareleri toplamı, farklı 2 kenarının kareleri toplamının iki katıdır.
|AB|=a, |AD|=b, |AC|=e, |BD|=f olmak üzere
İspat
ADB üçgeninde kenarortay teoremi uygularsak ve bulduğumuz denklemi düzenlersek
Aynısını ABC üçgeni için de yaparsak aynı sonuca varabiliriz.
Paralelkenarda Alan
Bir paralelkenarın alanı 2 farklı yöntemle bulunabilir.
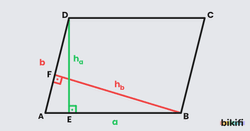
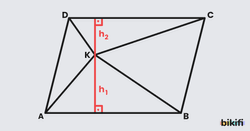
1. Taban çarpı yükseklikten bulabiliriz. Taban olarak iki farklı kenarı da alabilir, yüksekliğimizi de ona göre belirleriz.
2. Sinüsle alan formülünü kullanabiliriz. Normalde bu formül üçgenlerde kullanılır fakat paralelkenarın BD köşegenini çizdiğimizde iki eşit üçgene bölüneceğinden asıl formüldeki ikiye bölme işlemini burada uygulamayız.
Özellik 1
Bir paralelkenarda köşegenler paralelkenarı 4 eşit alana ayırır.
İspat
Temele indiğimizde köşegenler paralelkenarı iki eşit parçaya ayırdığı için iki köşegen 4 eşit parçaya ayırır gibi bir yorum yapabiliriz.
Matematiksel kısma geldiğimizde ise ABCD paralelkenarını içinde bulunan ABC ve ACD üçgenlerine ayırdığımızda bu üçgenlerin hem yükseklik hem de taban uzunlukları eşit olduğundan alanları da eşit olacaktır.
Bu üçgenlerden birini ele aldığımızda örnek olarak ABC üçgeni içerisindeki ABE ve BCE üçgenlerini incelediğimizde yüksekliği B noktasından indirdiğimizde eşit uzunlukta, taban uzunluklarını incelediğimizde ise AE ve EC uzunlukları da eşit olduğundan bu iki üçgenin de alanını eşit buluruz. Aynı şeyi ACD üçgeni içerisinde de uygulayabiliriz.
Özellik 2
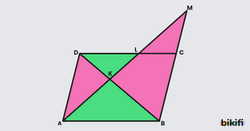
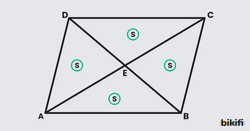
Bir paralelkenarın içinden herhangi bir nokta seçilip köşelerle birleştirildiğinde oluşan üçgenlerden karşılıklı duranların alanları toplamı birbirine eşit ve paralelkenarın alanının yarısına eşittir.
İspat
İlk olarak karşılıklı duran AKB ve CKD üçgenlerini ele alalım. Bu üçgenlerin alanlarını bulup topladığımızda paralelkenarın alanının yarısını elde ederiz. Paralelkenarın alanının yarısı bu üçgenlere aitse diğer karşılıklı duran üçgenler de yarısına eşit olacaktır. Aşağıda için yaptığımız işleri için de aynı şekil yapabiliriz.
Özellik 3
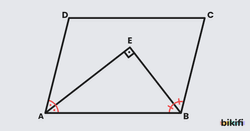
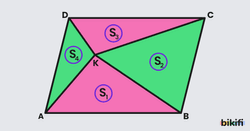
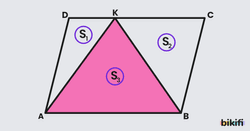
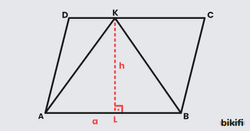
Bir paralekenarda kenar üzerinden alınan nokta köşelerle birleştirildiğinde oluşan üçgenlerden ortadaki büyük üçgen kenarında duran iki üçgenin alanına ve paralelkenarı alanının yarısına eşittir.
Bu özellik bir önceki özellikle bağdaştırılabilir. Paralelkenarın herhangi bir yerinden alınan nokta kenar üzerinde olduğundan büyük üçgenin karşısındaki üçgen yok olmuş fakat onun alanı bu büyük üçgene geçmiş gibi düşünebilirsiniz.
İspat
AKB üçgeninin yüksekliği ve tabanı paralelkenarınkilere eşittir. Üçgende bu değerleri çarptıktan sonra ikiye böldüğümüz için K noktası DC kenarının neresinde olursa olsun AKB üçgeninin alanı paralelkenarın alanının yarısı olacaktır. Aynı şekilde K noktası yandaki kenarlardan birinde de olabilir. Örnek olarak K noktasını AD kenarı üzerinde bir yerde düşünürsek bu sefer yüksekliği BC kenarına indireceğiz ve o zaman da üçgenin alanını paralelkenarın alanının yarısı olarak bulacağız.