Kosinüs Teoremi Formülü
Kosinüs teoreminin bir formülü vardır ve bu formül için yeteri kadar bilgi verildiğinde eksik olan kenar uzunluğu veya açıyı bulabiliriz.
Aşağıda kenar uzunlukları a, b, c ve bu kenarları gören iç açılarına sahip bir ABC üçgeni bulunmaktadır. Üçgenin altında ise bu üçgen örnek alınarak her kenarı için ayrı yazılmış kosinüs teoremi bulunmaktadır.

Yukarıdaki 3 formül de aynıdır. Daha iyi canlandırma adına üçgenin her kenarı için ayrıca yazılmıştır. Bu formül üzerinden bir üçgenin iki kenar uzunluğu ve bu kenarların arasında bulunan açıyı kullanarak üçüncü kenarı bulabiliriz.
Tam tersi bir yolla 3 kenarı da bilinen bir üçgenin herhangi bir açısını bulabiliriz. Bulmak istediğimiz açının karşısındaki kenarı formülde a yerine koyup diğer kenarları da b ve c yerine koyarsak formülde tek bilinmeyen istediğimiz açının kosinüsü olacaktır. İşlemler sonucu istediğimiz açının kosinüsünü bulduktan sonra oradan açıya geçebiliriz.
Kosinüs Teoremi İspatı
Peki bu formülü nasıl bulduk? Formülün nereden ve nasıl bulunduğunu, temel mantığını bilirsek formülü unuttuğumuzda bile mantığı oturduğu için yine sonuca bir türlü varabiliriz. Şimdi aşağıda formülü kendimiz bulalım.
Kosinüs teoreminin ispatını uzaklık ve trigonometri yöntemleriyle iki farklı şekilde bulabiliriz.
Uzaklık Yöntemi İle İspat
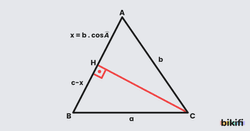
Aşağıdaki ABC üçgeninde C köşesinden AB kenarına bir dikme indirilmiş ve kesişim noktasına H noktası adı verilmiştir. H noktasının üzerinde kalan kısım yani AH uzunluğuna x dediğimiz zaman aşağıda kalan BH uzunluğu (c-x) olacaktır.
AHC üçgenine baktığımız zaman açısının kosinüsü komşu bölü hipotenüsten olarak buluruz. Bu eşitlikte x uzunluğunu yalnız bırakırsak sonucuna varırız. Aynı yöntemle HC kenarının uzunluğunu olarak buluruz. BH kenarına (c-x) uzunluğunda buldğumuz x’i de yerleştirelim.
BHC üçgeninin bütün kenarlarını tek bir açıya bağlı olacak şekilde bulduğumuza göre artık hipotenüs formülünü uygulayarak bir eşitlik elde edeceğiz.
Trigonometri Yöntemi İle İspat
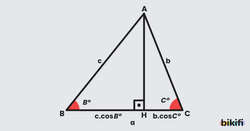
Aşağıdaki ABC üçgeninde A köşesinden BC kenarına bir dikme indirilmiş ve kesişim noktasına H noktası adı verilmiştir.
ABH üçgenindeki trigonometrik bağıntılardan BH uzunluğu , ACH üçgeninde ise CH uzunluğunu olarak buluruz. Şimdi gerekli uzunluklar bulunduğuna göre aşağıdaki adımları izleyelim.
- Bulduğumuz BH ve CH uzunluklarını toplayarak kenarını bulalım.
- Her iki tarafı da ile çarpalım.
- Aynı adımları diğer kenarlara dikme indirmiş gibi düşünerek oluşacak eşitlikleri yazalım.
- Son bulduğumuz iki eşitliği toplayalım.
- Bu eşitliği de düzenleyelim.
- Eşitliğin sol tarafına baktığımızda ‘ye eşit olduğunu görürüz. ‘yi yerine yazdığımızda formülün son haline ulaşırız.
Kosinüs Teoremi Örnekleri
Örnek 1
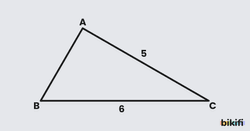
Şekildeki ABC üçgeninde; ve olduğuna göre değerini bulunuz.
Çözüm
ABC üçgeninde bütün kenar uzunlukları verildiğine göre istediğimiz bir kenarı seçip kosinüs teoremi uygulayarak karşısındaki açının kosinüs değerine ulaşabiliriz. BC kenarını ana kenar olarak belirlersek değerine ulaşabiliriz.
Örnek 2
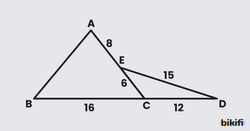
Yukarıdaki şekilde B, C, D noktaları ve A, E, C noktaları doğrusal olmak üzere. olduğuna göre, uzunluğunun kaç cm olduğunu bulunuz.
Çözüm
olarak belirlersek önce ECD üçgeninde kosinüs teoremi uygulayarak açısının kosinüs değerine ulaşır, sonrasında ABC üçgenine geçeriz. Bu noktadan sonra ABC üçgeninin 2 kenarını ve ortalarında bulunan açının kosinüsünü bilir durumda olacağız. Artık ABC üçgeninde de kosinüs teoremi uygulayarak uzunluğuna ulaşırız.
- ECD üçgeninde kosinüs teoremi uygulayalım.
- değerini bulduğumuza göre artık ABC üçgeninde kosinüs teoremini uygulayabiliriz.
- Hatırlatma: