Dörtgenlerde Açı ve Uzunluk Bağıntıları
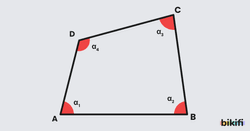
Özellik 1: Dörtgenlerde İç Açı
n kenarlı bir çokgenin iç açıları toplamını bir önceki konu olan çokgenler konusunda (n-2)x180° bulmuştuk. O zaman bir dörtgenin iç açılarının yerine 4 yazarak 360° olduğunu bulabiliriz.
(4-2)x180° = 360°
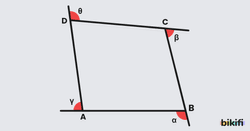
Özellik 2: Dörtgenlerde Dış Açı
Her çokgende olduğu gibi bir dörtgenin dış açı ölçüleri toplamı 360° dir. Çokgenler konusunda bunu da yeterince açıklamıştık.
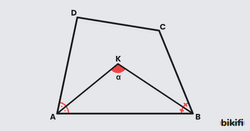
Özellik 3: Dörtgenlerde Komşu Açıortay Kuralı
Bir dörtgende komşu iki açının açıortayları arasında kalan açının ölçüsü, diğer iki açının ölçüleri toplamının yarısıdır.
İspat
Açıortaylardan birinin yarısına a°, diğerinin yarısına b° değerini verirsek;
AKB üçgeninin iç açıları toplamından, (1)
ABCD dörtgeninin iç açıları toplamından, (2)
denklemlerini elde ederiz.
1. denklemi ikiyle çarptığımızda (3) buluruz.
2. ve 3. denklemleri karşılaştırdığımızda ise 2. nın aslında C ve D köşelerindeki açıların toplamına eşit olduğunu görürüz.
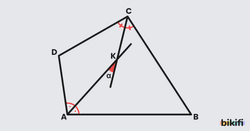
Özellik 4: Dörtgenlerde Karşılıklı İki Açıortay
Bu seferde Bir dörtgende karşılıklı iki açının açıortayları arasındaki dar açının ölçüsü, diğer iki açının ölçüleri farkının mutlak değerinin yarısıdır.
İspat
Açıortaylardan birinin yarısına a°, diğerinin yarısına c° değerini verirsek;
AKCD dörtgeninin iç açıları toplamından, (1)
ABCD dörtgenin iç açıları toplamından, (2)
denklemlerini elde ederiz.
1. denklemi ikiyle çarpıp gerekli sadeleştirmeleri yaptığımızda (3) denklemini buluruz.
2. ve 3. denklemleri karşılaştırdığımızda ise ‘ye eşit buluruz.
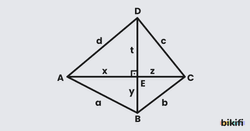
Özellik 5: Köşegenleri Dik Kesişen Dörtgenler
Köşegenleri dik kesişen dörtgenlerde, karşılıklı kenarların uzunluklarının kareleri toplamı eşittir.
Bu özelliğin temeli üçgenlerde pisagor teoremine dayanır.
Buradan şu sonucuna varabiliriz;
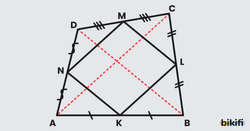
Özellik 6: Dörtgenlerde Kenar Orta Noktalar
Bir dörtgenin kenarlarının orta noktalarını birleştirirsek ortasında bir paralelkenar dörtgen ve aşağıdaki eşitlikler oluşur.
Bu özelliğin temeli üçgenlerde benzerliğe dayanır. Eğer anlamadıysanız üçgenlerde eşlik ve benzerlik konusuna göz atabilirsiniz.
Dörtgende Alan Bağıntısı
Özellik 1
Bir dörtgenin alanı, dörtgenin köşegen uzunları ile köşegenler arasında kalan açının sinüs değeriyle çarpımının yarısına eşittir.
İspat
Üçgenlerde alan bulma yöntemlerinden biri sinüs teoremidir. Dörtgenin köşegenlerini çizdiğimizde aslında 4 tane üçgen elde etmiş oluruz. Bu 4 üçgenin alanını topladığımızda ise ABCD dörtgeninin alanını buluruz.
olduğu için aşağıda yazmamız gereken yerlere de direkt yazacağız.
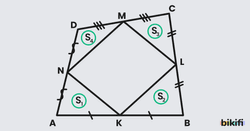
Özellik 2
Bir dörtgende kenarların orta noktaları birleştirildiğinde köşelerde oluşan üçgenlerden karşılıklı duran üçgenlerin alanları toplamı birbirine eşittir. Ayrıca bunlar ortada oluşan dörtgenin alanının yarısı, tüm dörtgenin alanının ise 4’te 1’i kadardır. Ayrıca akılda kalıcı olsun diye köşelerdeki bütün üçgenlerin alanlarının toplamı ortadaki KLMN dörtgeninin alanına eşit diyebiliriz.
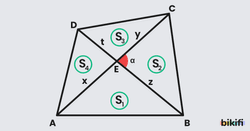
Özellik 3
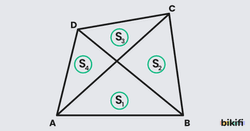
Bir dörtgenin köşegenleri çizildiği zaman oluşan 4 tane üçgenden karşılıklı üçgenlerin alanları çarpımı birbirine eşittir.
Alan sorularında genellikle böyle bir şekil çıktığında karşımıza köşegenlerden bazı parçaların uzunlukları ve belli üçgenlerin alanları verilir. Bu durumlarda yan yana duran üçgenlerin yükseklikleri aynı olacağından tabanları arasındaki oranlardan alanları arasında geçiş yapıp bu özellikle de geri kalan üçgenlerin alanlarını bulup tüm dörtgenin alanına ulaşabilirsiniz.