Doğrusal olmayan üç veya daha fazla noktanın doğrusal çizgilerle (birbirlerinin üstünden geçmeyecek şekilde) birleşerek oluşturduğu kapalı şekle çokgen denir. Çokgenlerin köşe ve kenar sayıları eşit olur. Çokgenler kenar sayılarına göre isimlendirilir. Örnek olarak dört kenarlı bir çokgene dörtgen, yedi kenarlı çokgene ise yedigen diyebiliriz.
Çokgen ve Temel Elemanları
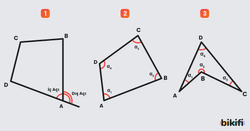
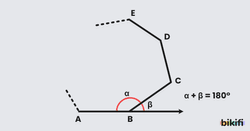
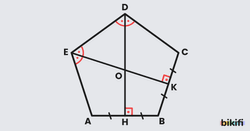
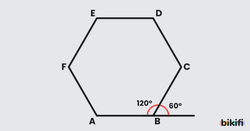
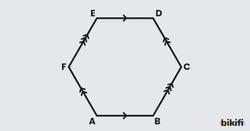
Bir çokgenin herhangi bir köşesine baktığımızda, iki kenarının arasında kalan açılardan çokgenin iç bölgesine doğru bakan açıya iç açı denir. Bu açıların komşu bütünleri olan açılara ise dış açı denir (Görsel 1).
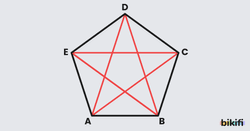
Bir çokgenin her bir açısının ölçüsü 180° ‘den küçük ise dış bükey (konveks) çokgen (Görsel 2), açılardan en az birinin ölçüsü 180° ‘den büyük ise iç bükey (konkav) çokgen (Görsel 3) denir.
Bir çokgende komşu olmayan iki köşeyi birleştiren doğru parçasına köşegen denir.
n kenarlı bir çokgende köşegen sayısı:
İspat
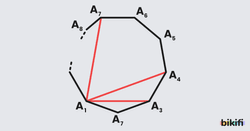
Bir köşegen 2 köşenin birleştirilmesinden oluştuğu için, köşegeni çizmek için iki tane köşe seçmek gerekir. n kenarlı bir çokgen için n tane köşesi olduğu için n köşeden 2 tane seçme işlemini n’nin 2’li kombinasyonunu () alarak bulabiliriz ancak bunlardan n tanesi çokgenimizin kenarları olduğu için bunu çıkartmalıyız.
- olarak bulunur.
Çokgende Açı Bağıntıları
İç Açılar
n kenarlı bir çokgenin iç açı ölçüleri toplamı (n-2)x180° dir.
Örnek olarak bir altıgen için iç açı ölçülerini (6-2)x180° den 720° olarak buluruz.
İç Açı Formülü İspatı
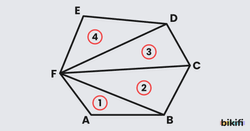
Hepimiz üçgenlerin iç açı ölçülerinin toplamının 180° olduğunu biliriz. Üçgen dışındaki diğer çokgenlerde ise gizli üçgenler bulunur. Bu üçgenleri ortaya çıkardığımızda aslında ne kadar üçgen varsa o kadar 180° vardır. n kenarlı bir çokgenin bir köşesinden bütün köşelere köşegen çizdiğimizde çokgen (n-2) tane üçgene ayrılır. (n-2)’yi 180° ‘yle çarptığımızda çokgenin iç açı ölçülerinin toplamını bulabiliriz.
Örnek olarak aşağıdaki altıgenin bir köşesinden diğer köşelere köşegenler çizdiğimizde 4 tane üçgen ortaya çıkar. Yani her üçgenin iç açı ölçüleri toplamı 180° olduğu için 4×180° den 720° olarak bulabiliriz.
Üçgenlerin iç açı ölçülerinin toplamının nasıl 180° olduğunu merak ediyorsanız Üçgenlerde Temel Kavramlar yazımıza tıklayarak göz atabilirsiniz.
Dış Açılar
n kenarlı bir çokgenin dış açı ölçüleri toplamı her zaman 360° dir.
Dış Açı Formülünün İspatı
n kenarlı bir çokgen için;
- iç ve dış açı ölçüleri toplamı nx180°
- iç açı ölçüleri toplamı (n-2)x180°
olduğunu biliyoruz.
O zaman iç ve dış açılarının toplamından(nx180°) iç açılarının toplamını((n-2)x180°) çıkartırsak dış açılarının toplamını bulabiliriz.
n’ler birbirini götürdüğü için kenar sayısından bağımsız olarak her zaman sonuç 360 çıkar.
Düzgün Çokgenler
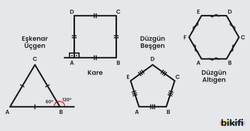
Bütün kenar uzunlukları birbirine eşit ve bütün açılarının ölçüleri birbirine eşit olan çokgenlere düzgün çokgen denir.
Düzgün Çokgenlerde Açı ve Kenar Bağıntıları
n kenarlı bir çokgen için;
Yukarıda bir çokgenin iç açılarının toplamını formülünden bulabildiğimizi söylemiştik. Düzgün çokgenlerde her bir iç açısı birbirine eşit olduğundan çokgenin iç açıların toplamını kenar sayısına bölersek çokgenin iç açılarını bulmuş oluruz.
Düzgün çokgenin bir iç açı ölçüsü:
Düzgün çokgenlerde bütün iç açılarının birbirine eşit olduğu gibi dış açıları da birbirine eşit olacaktır. Yukarıda bütün çokgenlerin dış açılarının toplamının 360° olduğunu söylemiştik. Bu yüzden 360° ‘yi çokgenin kenar sayısına böldüğümüz zaman bir dış açısını buluruz.
Düzgün çokgenin bir dış açı ölçüsü:
Sağlama yapmak istersek bir düzgün çokgen için bir iç açısıyla bir dış açısının toplamı 180° olacaktır. Yukarıda verdiğimiz formülleri toplarsak yine 180° bulacağız.
n bir tek sayı ise bir köşeden çizdiğimiz açıortay, karşı kenarı dik keser ve çokgeni eşit iki parçaya böler (simetri ekseni).
n bir çift sayı ise karşı köşeleri birleştiren doğru parçası açıortaydır ve şekli eşit iki parçaya böler (simetri ekseni). Ayrıca çokgenin karşılıklı kenarları birbirine paraleldir.
Genel bilgileri verdikten sonra karşımıza çok çıkan çokgenleri inceleyeceğiz. Dörtgenler çok fazla ayrıntı içerdiğinden şimdi düzgün beşgen ve altıgeni inceleyip, daha sonra dörtgenleri ayrı bir başlıkta göreceğiz.
Düzgün Beşgen
Bütün kenarları ve iç açıları eşit olan beşgene düzgün beşgen denir.
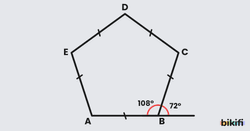
- İç açı ölçüsü:
- Dış açı ölçüsü:
Düzgün Beşgen Özellikleri
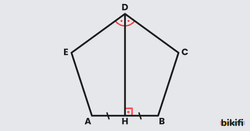
Özellik 1: Düzgün beşgen bir köşeden çizilen açıortay karşı kenarı dik keser. Düzgün beşgenin bütün iç açıortaylarının uzunlukları birbirine eşittir ve hepsi tek bir noktada kesişir.
Özellik 2: Düzgün beşgende bütün köşegen uzunlukları birbirine eşittir.
- olur.
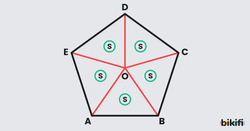
Özellik 3: Düzgün beşgenin iç açıortaylarının kesiştiği nokta beşgenin ağırlık merkezidir. Ağırlık merkeziyle köşelerin birleştirilmesiyle ortaya birbirine eş 5 üçgen oluşur.
- ise,
Düzgün Altıgen
Bütün kenarları ve iç açıları eşit olan altıgene düzgün altıgen denir.
- İç açı ölçüsü:
- Dış açı ölçüsü:
Düzgün Altıgen Özellikleri
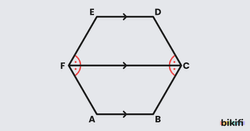
Özellik 1: Düzgün altıgenin karşılıklı kenarları paraleldir.
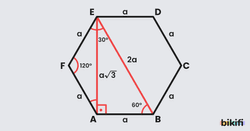
Özellik 2: Düzgün altıgenin iki farklı uzunluğa sahip köşegeni vardır. aynı köşeden çizdiğimiz biri kısa diğeri uzun iki köşegen çizdiğimizde oluşacak 30°-60°-90° üçgeninden köşegenlerin uzunluklarını bulabiliriz.
- ise,
- EAB üçgeni 30°-60°-90° üçgenidir.
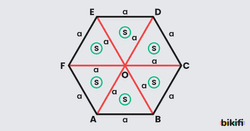
Özellik 3: Düzgün altıgenin karşılıklı köşelerini birleştiren bütün uzun köşegenleri çizildiğinde altıgen birinin aynısı 6 eşkenar üçgene ayrılır.
- ise,
- ise,
Bir kenar uzunluğu a olan eşkenar üçgenin alan formülünü altıyla çarparak altıgenin alanını buluruz.
Düzgün Çokgenlerde Alan Bağıntısı
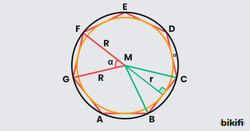
n kenarlı bir düzgün çokgenin ağırlık merkezi, iç teğet ve çevrel çemberinin merkezidir.
Merkezden her bir köşeye doğrular çizdiğimizde çokgenin içinde kenar sayısı kadar üçgen oluşur. Bu üçgenlerden birinin alanını bulup kenar sayısıyla çarptığımızda düzgün çokgenin alanını buluruz. Üçgenin alanını iki farklı yöntemle bulabiliriz.
- İç teğet çemberin yarıçapı olan üçgenin yüksekliği, düzgün çokgenin bir kenar uzunluğu() ise üçgenin tabanıdır. Bu iki değeri çarpıp ikiye böldüğümüzde bir üçgenin alanını buluruz. Üçgenin alanını kenar sayısıyla çarparak düzgün çokgenin alanına ulaşırız.
- Üçgende alan bulmada diğer yöntem ise sinüs teoremidir. Teoreme göre üçgenin iki kenarı() ve bu iki kenar arasındaki açının sinüsü() çarpılıp ikiye bölündüğünde üçgenin alanını verir. Yine bulduğumuz alanı kenar sayısıyla çarparsak düzgün çokgenin alanına ulaşırız.
Yukarıdaki alan bulma yöntemlerinin formüllerini yazalım.