Yönlü Açılar

Bikifi Instagram'da

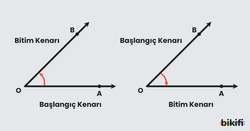
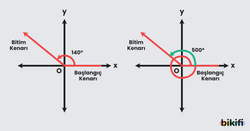
Aşağıdaki görselde başlangıç ve bitim kenarına göre açının yönü okla gösterilmiştir.

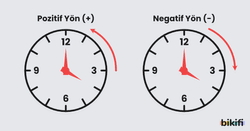
Saatin dönme yönünün tersi olan yöne pozitif yön, aynı olan yöne negatif yön denir.

Açı Ölçü Birimleri

Açının kenarları arasındaki açıklığa açı denir ve bir açının büyüklüğünü ve küçüklüğünü ifade etmek için bazı açı ölçü birimlerini kullanırız. Yaygın olarak kullandığımız açı ölçme birimleri derece ve radyandır.

Derece

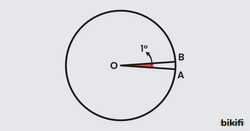
Bir çember çevresi 360 eş parçaya bölündüğünde her bir yay parçasını gören merkez açının ölçüsüne 1 derece denir. Derece (°) sembolü ile gösterilir.

Daha da küçültmek gerekirse

• 1°, 60 dakikaya karşılık gelir. Dakika (‘) sembolü ile gösterilir.
• 1′, 60 saniyeye karşılık gelir. Saniye (“) sembolü ile gösterilir.

1° = 60′ = 3600″ = 59′ 60″

Radyan

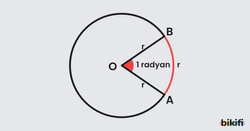
Bir çemberde , yarıçap uzunluğundaki yayı gören merkez açının ölçüsüne 1 radyan denir. Radyan (rad) şeklinde gösterilir.

Radyan açı ölçü birimine göre merkez açının tamamı radyan eder.

Bunun açıklaması çemberin çevresi olup, bunun herbir r uzunluğu 1 radyan ettiğine göre toplam çevreyi r’ye bölersek merkez açının kaç radyan olduğunu bulabiliriz. Bunun sonucunda merkez açının radyan olduğu sonucuna ulaşırız.

Bir tam çemberin merkez açısının ölçüsünün hem 360° hem de 2 radyan olduğunu öğrendik.

bağıntısı elde edilir.

Bu bağıntıda elimizde bulunan derece cinsinden ölçüyü D yerine koyup R’yi bularak aynı açının radyan cinsinden ölçüsünü elde edebiliriz. Aynı mantıkla tam tersini uygulayarak radyanın derece karşılığını da bulabiliriz.

Esas Ölçü

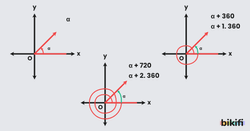
Başlangıç ve bitim kenarları aynı olup ölçüleri farklı olan açılara denk açılar denir. Denk açılara 140° ile 500° açılarını örnek olarak verebiliriz. Koordinat düzleminde açıların başlangıç kenarlarını x ekseni olarak alırsak 140 derece ilerleyince bir bitim kenarı bulunacak, fakat 500° nin bitim kenarını bulurken 360° sonra bir turunu tamamlayacak ve sonrasında bir 140° daha ilerleyerek aynı yerde bitim kenarı olacak.

Tüm bu denk açılardan 0° ile 360° arasında olan açıya bu açıların esas ölçüsü denir.

360° büyük açıların esas ölçülerini bulmak için bu açının içinde ne kadar 360° varsa çıkartabildiğimiz kadar çıkartırız. Bunun diğer bir yolu elimizdeki açıyı 360° ye bölerken kalan kısım bizim esas ölçümüz olacaktır. Aşağıdaki görselde esas açısı olan 3 adet denk açı gösterilmiştir.

Radyan cinsinden incelediğimizde ise ya sürekli 2 çıkartarak ya da açıyı ‘ye bölüp kalanı alarak esas açıya ulaşabiliriz.

Negatif açılar için yine aynı taktiklerle açı ölçüsü 0° ile -360° veya 0 rad ile radyan arasına indirdiğimizde üzerine bir daha 360° veya radyan ekleyerek bu açının pozitif karşılığını alırız. Bulduğumuz bu sayı elimizdeki negatif açının esas ölçüsü olur.