Üstel fonksiyonda bir sayının sürekli katlanarak artması veya azalması durumunu bir örnekle açıklamamız gerekirse, 1 sayısını her seferinde 3 katına çıkarak bu hareketi 5 defa yaparsa her seferinde 3 ile çarpıldığı için 5 defa çarptığımız zaman 35 sayısını elde ederiz. Ayrıca bunu tersten düşünüp her seferinde 3’e bölerek 5 defa ilerlersek bu sefer elimizde 3-5 olacaktır. Başlangıçta 1 yerine herhangi bir x sayısı olsaydı bu sefer x.35 veya x.3-5 olacaktı.
şeklindeki fonksiyona üstel fonksiyon denir. Burada a sayısı üstel fonksiyonun tabanı, x ise üs olarak adlandırılır. a sayısı 1’den farklı pozitif reel sayı, x ise herhangi bir gerçek sayı olabilir.
Üslü İfadelerin Özellikleri
Üslü ifadelerin basit ama birçok özelliği vardır. Şimdi aşağıda bu özellikleri inceleyelim.
(Aşağıda yazanlar bu şartlara göre doğrudur)
a) Bir sayının üssü 0 ise sonuç her zaman 1’dir.
b) Aynı sayının iki farklı üslü ifadesi çarpım durumundaysa bu sayının üstüne üsleri toplayarak yazabiliriz.
c) Aynı sayının iki farklı üslü ifadesi bölme durumundaysa bu sayının üstüne payın üssünden paydanın üssünü çıkartarak yazabiliriz.
d) Bir sayının üssü varken paranteze alınıp bir daha üssü alınmışsa üsleri çarparak bu sayının üstüne yazabiliriz.
e) İki farklı sayı çarpım durumundayken ortak bir üs varsa bu üs iki sayının da üstüne yazarak çarpabiliriz.
f) iki farklı sayı bölüm durumundayken ortak bir üs varsa bu üs iki sayının da üstüne yazarak ay şekilde bölebiliriz.
g) Bir sayının üssü negatifse bu sayının çarpmaya göre tersini alarak yani pay ve paydanın yerini değiştirerek üssünü pozitif yapabiliriz.
h) Tabanı 1 ve -1 olmayacak şekilde, aynı sayı üzerinde farklı harflendirilmiş iki üslü ifade birbirine eşitse bu üsler kesinlikle birbirine eşittir.
Üstel Fonksiyonun Özellikleri
Yukarıdaki üslü ifadelerin özelliklerini kullanılarak üstel fonksiyon (f(x)=ax) özelliklerini aşağıda inceleyelim.
a) Üstel fonksiyonda sıfırıncı kuvvet her zaman 1’e eşittir.
b) Üstel fonksiyonda birinci kuvvet tabanın kendisine eşittir.
c) İki sayının toplamı şeklinde yazılan üstel fonksiyon, bu iki sayısının tek tek fonksiyonunun çarpımıyla aynı sonucu verir.
d) İki sayının çarpımı şeklinde yazılan üstel fonksiyon, bu sayılardan birini diğer sayının fonksiyonunun üstüne yazılmış haliyle aynı sonucu verir.
e) Üstel fonksiyonun içindeki negatif sayıyı fonksiyonun çarpmaya göre tersini alarak içini pozitife çevirebiliriz.
Örnek: n sayısı pozitif tam sayı olmak üzere f(x)=3x+2 ve f(1).f(2).f(3)….f(n)=273n olduğuna göre n sayısı kaçtır?
Hatırlatma:
- Çarpım durumunda bulunan üstel fonksiyonları fonksiyonda yerine koyup yazdığımızda tabanı 3 olan ve üsleri 3’ten başlayarak artarak gitmektedir. Burada tabanlar aynı ve hepsi çarpım durumunda olduğu için üslerini toplarız.
- Üsler ardışık sayılar olduğu için yukarıdaki ardışık sayıların toplam formülünü kullanırız fakat sonuçtan 1 ve 2 olmadığı için çıkartmaya unutmamalıyız.
- Bulduğumuz bu sonuç bize zaten sorunun başında verilen sonuca eşit olacağından onu da 3 tabanına çevirerek üsleri birbirine eşitleyebiliriz.
Burada n sayısı sıfır olamayacağı için n=13 olarak buluruz.
Üstel Fonksiyonun Grafiği
Bir f(x)=ax (a, 1’den farklı pozitif reel sayıdır) üstel fonksiyonunun grafiğini çizmek istersek 2 farklı grafik ortaya çıkacaktır. Bunlar a tabanının 1’den küçük ve büyük olduğu durumlardır.
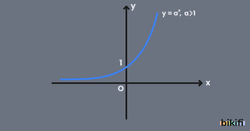
Artan Fonksiyon Grafiği (a>1)
Öncelikle a tabanının 1’den büyük olduğu durumu incelersek üssü sıfır olduğunda 1’e eşit olacak ve üs arttıkça sonuç katlanarak artacaktır. Fakat üs negatif yönde arttıkça sonuç 1’den 0’a doğru sonsuza kadar gidecektir. a>1 durumunda f(x)=ax üstel fonksiyonuna artan fonksiyon denir. Aşağıda artan fonksiyonun grafiği verilmiştir.
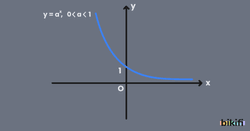
Azalan Fonksiyon Grafiği (a<1)
Şimdi ise a tabanının 1’den küçük olduğu durumlara baktığımızda ilk olarak üssü sıfır durumu aynı şekil 1’e eşit olacaktır. Üs pozitif yönde arttığında payda paydan büyük olduğu için üs arttıkça aradaki fark açılacak yani sonuç 1’den 0’a doğru giderek küçülecektir. Fakat üs negatif olursa pay ve payda yer değiştireceği için durum tam tersine döner ve üs negatif yönde büyüdükçe sonuç sonsuza doğru gidecektir. 1>a>0 durumunda f(x)=ax üstel fonksiyonuna azalan fonksiyon denir. Aşağıda azalan fonksiyonun grafiği verilmiştir.
Üstel fonksiyonların grafikleri tabandaki sayıya göre eğriliği değişse de genel olarak bu iki şekildedir.