Örnek olarak f(x)=cos(x) fonksiyonunun periyodunun T=2π olduğunu biliyoruz. Bunun anlamı bu fonksiyonun her 2π aralığında tekrar edecek olmasıdır. f(x)=cos(x) fonksiyonunun grafiğini çizmek istersek 2π uzunluğundaki bir aralığı bulduğumuz zaman geri kalan kısımları bu aralığın sağına ve soluna aynı aralığı kopyalayabiliriz. Bu yöntemle sinx, cosx, tanx ve cotx grafiklerini çizip yorumlayabiliriz.
Sinüs Fonksiyonunun Grafiği
f(x)=sin(x) fonksiyonunun periyodu T=2π ‘dir. Her 2π aralığında tekrar ettiği için bu uzunlukta istediğimiz bir aralığı seçelim. Bu aralığı [0,2π] olarak seçip fonksiyonun değerlerini bulup bunları grafikte …,[-6π,-4π],[-4π,-2π],[-2π,0],[0,2π],[2π,4π],[4π,6π],… aralıklarında tekrar edecek şekilde yerleştirebiliriz.
Sinüs Fonksiyonunun Belirli Açılarda Aldığı Değerler
| x | 0 | ||||
|---|---|---|---|---|---|
| y=sinx | 0 | 1 | 0 | -1 | 0 |
Bulduğumuz bu noktaları grafikte birleştirip aynı şekil sağa ve sola devam ettirdiğimizde karşımıza y=sinx grafiği çıkacaktır.
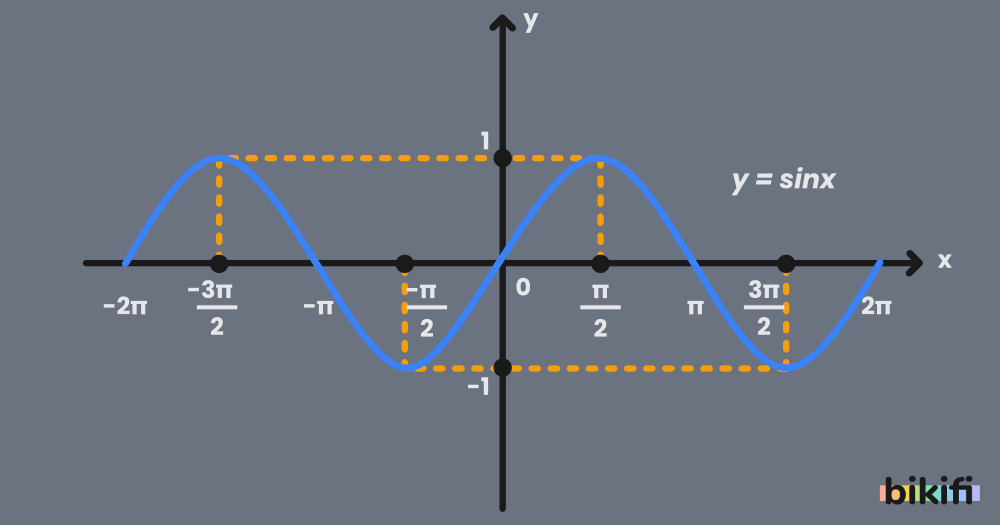
Grafiği incelediğimizde
, , , noktalarına baktığımızda verilen ikili noktalar orijine göre simetriktir. Orijine göre simetrik olan fonksiyonlara tek fonksiyon adı verilir ve sinüs tek fonksiyondur.
Tek fonksiyonlarda x değerinin işaretinin değişmesi y değerinin de işaretini değiştirir. Yani sinüs fonksiyonlarında x değerinin işaretini değiştirirsek sonuç sinüsün negatif değerine eşit olur. Aşağıda verilen denklem bütün sinüs fonksiyonları için geçerlidir. Bu durumu yukarıdaki noktalarda ve grafikte inceleyebilirsiniz.
Kosinüs Fonksiyonunun Grafiği
f(x)=cos(x) fonksiyonunun da periyodu T=2π ‘dir ve kosinüs fonksiyonu için de [0,2π] aralığındaki noktaları bulup sağına ve soluna aynı değerler eklenerek grafiği oluşturabiliriz.
Kosinüs Fonksiyonunun Belirli Açılarda Aldığı Değerler
| x | 0 | ||||
|---|---|---|---|---|---|
| y=cosx | 1 | 0 | -1 | 0 | 1 |
Bu değerleri grafiğe yerleştirelim.
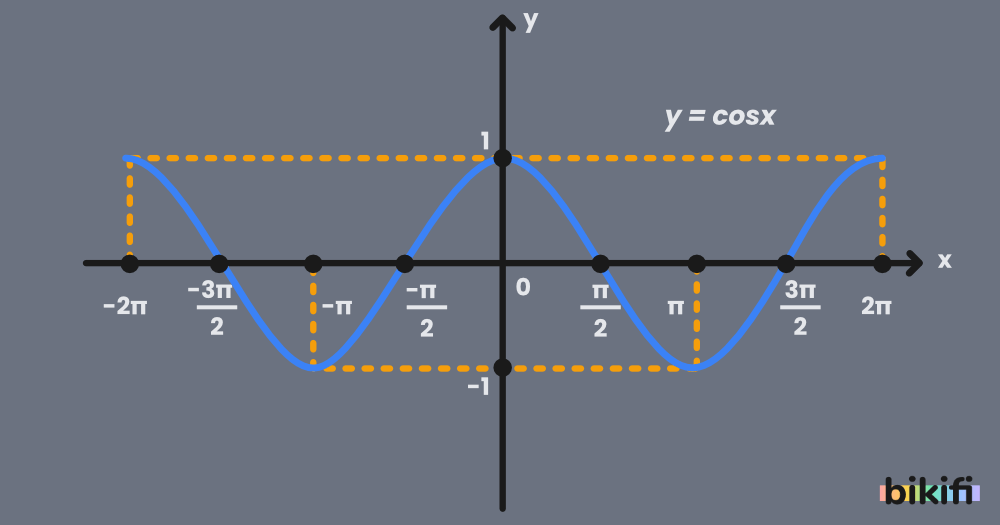
Grafiği incelediğimizde
, , , noktalarına baktığımızda verilen ikili noktalar y eksenine göre simetriktir. Bunun gibi y eksenine göre simetrik olan fonksiyonlara çift fonksiyon adı verilir ve kosinüs çift fonksiyondur.
Çift fonksiyonlarda x değerinin işaretini değiştirmek y değerinde hiçbir değişikliğe yol açmamaktadır. Böylelikle kosinüs fonksiyonu için x değerinin işaretini değiştirsek bile sonuçta bir değişiklik olmayacaktır. Aşağıda verilen denklem bütün kosinüs fonksiyonları için geçerlidir. Bu durumu yukarıdaki noktalarda ve grafikte inceleyebilirsiniz.
Tanjant Fonksiyonunun Grafiği
f(x)=tan(x) fonksiyonunun periyodu T=π ‘dir. Tanjant fonksiyonunun grafiğini oluşturmak için sinüs ve kosinüsten farklı olarak π kadar bir aralık seçeceğiz ve bu aralık tanjantı tanımsız yapan iki değer arasında seçmek mantıklı olacaktır. Bu nedenle aralığını seçersek bu aralığı daha sonra sağına ve soluna ekleyerek tanjant fonksiyonunun grafiğini elde edebiliriz.
Tanjant Fonksiyonunun Belirli Açılarda Aldığı Değerler
| x | 0 | ||||
|---|---|---|---|---|---|
| y=tanx | -1 | 0 | 1 |
Bulduğumuz bu değerleri grafiğe yerleştirip sağını ve solunu aynı şekil devam ettirirsek aşağıdaki grafiğe ulaşmış oluruz.
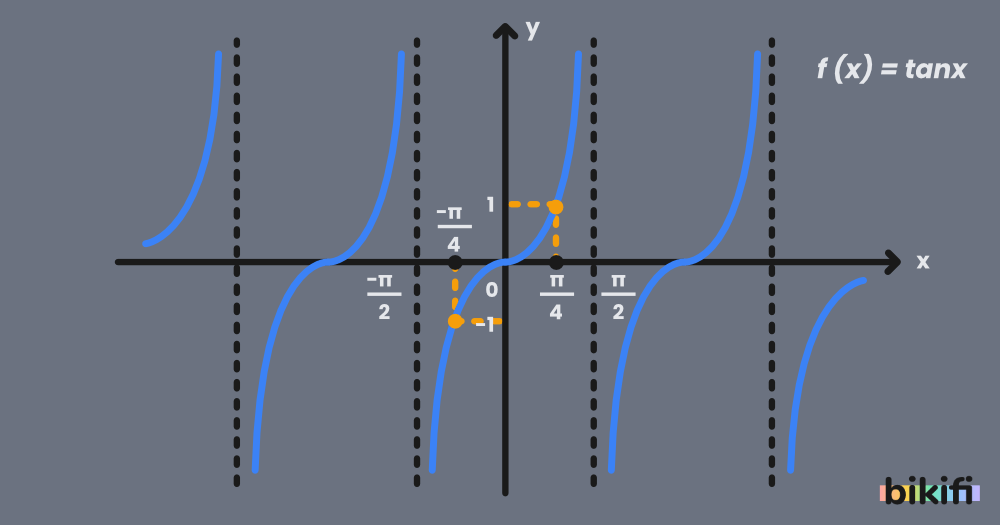
Grafiği incelediğimizde
veya x ekseninde herhangi bir noktanın pozitif veya negatifini aldığımızda sonuçların da aynı fakat farklı işaretli olduğunu göreceğiz. Buna göre tanjant fonksiyonunda noktalar orijine göre simetrik oluyor. Bu da demek oluyor ki aynı sinüs fonksiyonu gibi tanjant fonksiyonu da tek fonksiyondur ve x değerinin işaret değiştirmesiyle y değeri de işaret değiştirir. Aşağıda verilen denklem bütün tanjant fonksiyonları için geçerlidir. Bu durumu yukarıdaki grafikte inceleyebilirsiniz.
Kotanjant Fonksiyonunun Grafiği
f(x)=tan(x) fonksiyonunun periyodu da T=π ‘dir. Kotanjant fonksiyonunun grafiği için aynı tanjant fonksiyonunda yaptığımız gibi π kadar aralık seçeceğiz fakat kotanjantı tanımsız yapan değerler farklı olduğu için bu aralığı (0,π) seçebiliriz.
Kotanjant Fonksiyonunun Belirli Açılarda Aldığı Değerler
| x | 0 | ||||
|---|---|---|---|---|---|
| y=cotx | 1 | 0 | -1 |
Aynı şekil tabloyu grafiğe dönüştürelim.
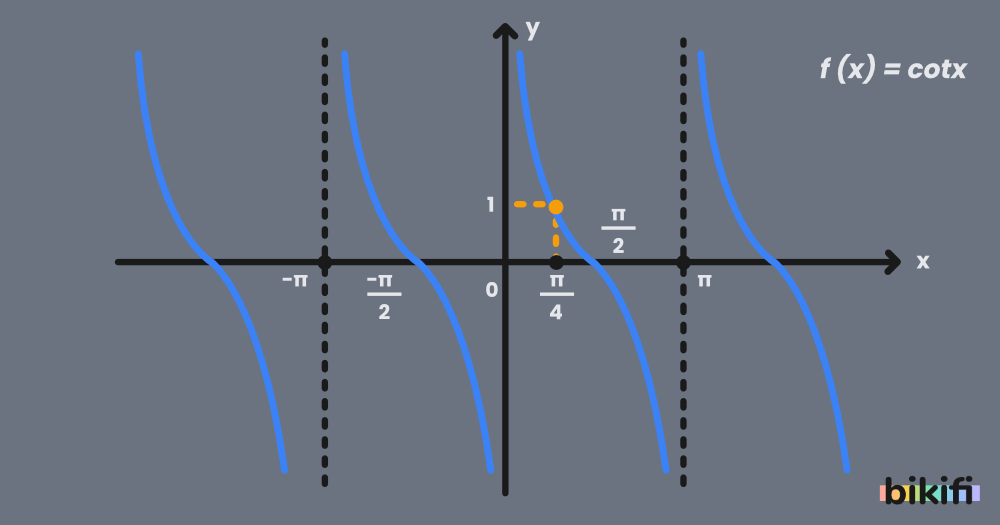
Grafiği incelediğimizde
Kotanjant fonksiyonunda noktaların orijine göre simetrik olduğu görülüyor. Bu durumda sinüs ve tanjant fonksiyonları gibi kotanjant fonksiyonu da tek fonksiyondur. Aşağıda verilen denklem bütün kotanjant fonksiyonları için geçerlidir. Bu durumu yukarıdaki grafikte inceleyebilirsiniz.
Trigonometrik Fonksiyonların Teklik Çiftlik Durumu
Yukarıdaki detaylı anlatımı özetlememiz gerekirse;
- Tek Fonksiyonlar: Eğer f(−x) = −f(x) ise f fonksiyonuna tek fonksiyon denir.
- Sinüs, tanjant, kotanjant ve kosekant tek fonksiyondur.
- Çift Fonksiyonlar: Eğer f(−x) = f(x) ise f fonksiyonuna çift fonksiyon denir.
- Kosinüs ve sekant fonksiyonu çift fonksiyondur.













