Trigonometrik fonksiyonlarda karmaşık işlemleri kolaylaştırmak ve çözümü daha kolay halde getirmek için toplam fark formüllerini kullanırız. Bu yazıda öncelikle toplam fark formüllerine değineceğiz. Ardından, bu formüllerin nereden bulunduklarını göstereceğiz. Formüllerin bulunuş mantığını anlamanız, aklınızda kalması bakımından fayda sağlayacaktır.
Toplam Fark Formülleri – Özet
Sinüs
Kosinüs
Tanjant
Kotanjant
Kosinüs Toplam Fark Formülleri
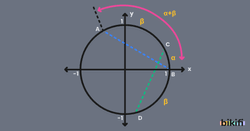
Kosinüsün toplam ve fark formüllerini bulmak için bazı eşitliklerden faydalanacağız. Aşağıda verilen görseldeki gibi bir çember üzerinde eşit uzunluğa sahip iki kiriş belirleyelim ve bu kirişler kesişiyor olsun. Bu kesişen kirişlerin ortak yay açısına , geri kalan yay açısına ise diyelim.
İki nokta arasındaki uzaklık formülünden kirişlerin uzunluğunu hesaplayıp birbirine eşitleyebiliriz. Bu kirişler öyle bir açıyla koyulmuştur ki |AB| kişinin uzunluğunu hesaplarken sinüs ve kosinüsün açıları ‘nın toplamı olacaktır fakat |CD| kirişi için bunu yaptığımızda ayrı bulunacaktır. Bu eşitliğin sonucunda ise bir toplam fark formülü elde etmiş olacağız.
Hatırlatma 1: İki nokta arasındaki uzunluğu hesaplama
Hatırlatma 2:
Hatırlatma 3:
AB kirişinin uzunluğu
CD kirişinin uzunluğu
Kiriş uzunlukları eşit olduğu için I. ve II. denklemlerin karesini alarak köklerden kurtulalım ve birbirine eşitleyelim.
Bulduğumuz bu formül kosinüsün toplam formülüdür. Bu formülde yazarsak kosinüsün fark formülünü elde edeceğiz.
Sinüs Toplam Fark Formülleri
Sinüsün toplam fark formüllerini bulmak için
eşitliğinden yararlanacağız.
Yukarıdaki eşitlikte x gördüğümüz yerlere yazıp kosinüs tarafını toplam fark formülüyle açarsak sinüs için de bir formül elde ederiz.
Bulduğumuz bu formül sinüse ait toplam formülüdür. Aynı kosinüste yaptığımız gibi bu formülde yazarsak bu sefer sinüsün fark formülünü elde ederiz.
Tanjant ve Kotanjant Toplam Fark Formülleri
Tanjant için toplam ve fark formülünü bulurken sinüs ve kosinüsün toplam fark formüllerinden yararlanacağız.
Bu formülde sadeleştirme yapıp daha düzenli hale getirebilmek için pay ve paydayı ifadesine bölelim.
Bulduğumuz bu formül tanjantın toplam formülüdür. Fark formülünü bulmak için yine yazarak bulabiliriz.
Kotanjantın toplam fark formülleri için ayrıca bir formül ezberlemeye gerek yoktur. Tanjantın çarpmaya göre tersi kotanjantı verdiği için kotanjantın toplam fark formüllerinin çarpmaya göre tersini alarak bulabiliriz.
Bir kotanjant formülünü yine de istersek bu formüllerde tanjantları kotanjanta çevirip düzenlersek kotanjantın toplam fark formüllerini elde ederiz.
Yukarıda kotanjantın toplam formülünü bulduk. Fark formülünü istersek bu formülde yazarak veya tanjantın fark formülünde aynı yolu izleyerek bulabiliriz.