Eşkenar Dörtgen
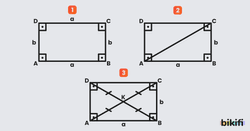
Karşılıklı kenarları birbirine paralel ve bütün kenarları eşit olan dörtgene eşkenar dörtgen denir. Diğer bir deyişle bütün kenarları eşit olan paralelkenar da diyebiliriz. Bu nedenle eşkenar dörtgenler bütün paralelkenar özelliklerini taşır.
Temelinde eşitliklerden dolayı fazladan bir kaç özelliği vardır.
- Her iki köşegen aynı zamanda açıortaydır. Bu açıların eşitliklerini Z kuralından ve kenarların eşitliklerinden bulabilirsiniz.
- . Bunun nedeni eşkenar dörtgenin ardışık iki açısının toplamının 180° olduğunu biliyoruz ve nereyi seçersek seçelim bu iki açının toplamının olduğunu göreceğiz.
- Köşegenler birbirini dik keser. Eşkenar dörtgen içinden aldığımız bir üçgende bir önceki özellikten bulduğumuz sayesinde merkezdeki açının 90° olduğunu bulabiliriz.
- Alan bulurken bütün yükseklikler ve tabanlar eşit olacaktır.
Dikdörtgen
Bütün iç açıları 90° olan dörtgene dikdörtgen denir. Dikdörtgenlerin karşılıklı kenarlarının birbirine paralel olduğu için iç açıları 90° olan bir paralelkenar olarak da düşünebiliriz. Bu nedenle dikdörtgenler bütün paralelkenar özelliklerini taşır.
Dikdörtgenin temel bir kaç özelliğini görelim.
- Karşılıklı kenar uzunlukları eşittir.
- Köşegen uzunlukları birbirine eşittir.
- Köşegenler birbirini ortalar ve iki eşit parçaya böler.
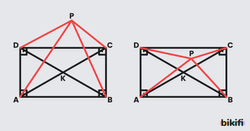
Dikdörtgenin iç veya dış bölgesindeki herhangi bir noktayı köşelerle birleştirdiğimiz zaman karşılıklı köşelere uzanan parçaların uzunluklarının kareleri toplamı birbirine eşittir.
Dikdörtgenin alanını ise kenarları birbirine dik olduğu için kısa ve uzun kenarı çarparak bulabiliriz.
Kare
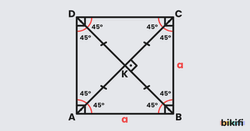
Bütün iç açıları 90° ve bütün kenar uzunlukları birbirine eşit olan dörtgene kare denir. Kare için bütün kenarları eşit dikdörtgen de diyebiliriz. Bu nedenle kareler de paralelkenar özelliklerini taşır.
Köşegenler için;
- Aynı zamanda açıortaydır.
- Uzunlukları birbirine eşittir.
- Birine dik ve ortalayarak iki eş parçaya bölerler.
- Uzunluğu bir kenarın katıdır.
Karenin alanı için bir kenarının karesi veya bir köşegeninin karesinin yarısını alarak da bulabiliriz.
Deltoid
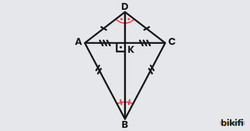
Deltoid diğer dörtgenlerden biraz farklı olup direkt olarak tanımlayıcı bir özelliğinden bahsedemeyiz fakat görünüşünü tabir etmek gerekirse taban uzunlukları eşit diğer kenar uzunlukları farklı olan iki ikizkenar üçgenin tabanlarından birleştirilmesi gibi bir görünüme sahiptir. Deltoid özelliklerini bu ikizkenar üçgenlerden alır.
ABCD deltoidi için;
- |AB|=|CB|,|AD|=|CD|
- ABC ve ADC ikizkenar üçgendir.
- Köşegenler dik kesişir.
- [BD] köşegeni [AC] köşegenini dik ortalar.
- [BD] köşegeni hem açıortay hem de deltoidin simetri doğrusudur.
Deltoidin alanını köşegenleri çarpıp yarısını alarak bulabiliriz. Bu özellik yine ikizkenar üçgenlerin alanlarını bulup toplamından gelmektedir.