Kümelerde Birleşim İşlemi
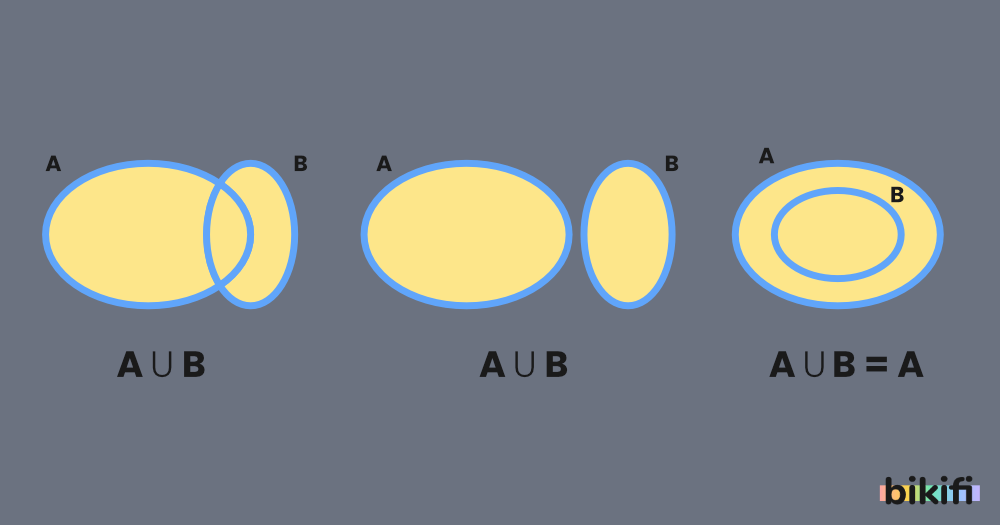
A ve B iki kümedir. A ile B kümelerinin oluşturduğu kümeye, A ve B kümesinin birleşim kümesi denir. A ∪ B şeklinde gösterilir.
A ∪ B = {x | x ∈ A veya x ∈ B} = { x | x ∈ A V x ∈ B} olarak ifade edilir.,
Mantıktaki V (veya) sembolü kümelerde ∪ (birleşim) işlemine karşılık gelir.
Birleşim İşleminin Özellikleri
- Bir kümenin kendisi ile birleşimi yine kendisidir. Buna tek kuvvet özelliği denir. A ∪ A = {x | x ∈ A V x ∈ A} = { x | x ∈ A } = A olduğunda A ∪ A = A olur.
- Bir kümenin boş küme ile birleşimi yine kendisidir. Bu durumda boş küme, birleşim işleminin etkisiz elemanıdır. A ∪ ∅ = {x | x ∈ A V x ∈ ∅} = A olduğundan A ∪ ∅ = ∅ ∪ A = A olur.
- Kümelerde birleşme işleminin değişme özelliği vardır. A ∪ B = {x | x ∈ A V x ∈ B} = { x | x ∈ B V x ∈ A} = B ∪ A olduğundan A ∪ B =B ∪ A olur.
- Kümelerde birleşim işleminin birleşme özelliği vardır. A ∪ (B ∪ C) = {x | x ∈ A V x ∈ (B ∪ C)} = { x | (x ∈ A) V (x ∈ B V x ∈ C)}
= {x | (x ∈ A V x ∈ B) V (x ∈ C)} = { x | (x ∈ (A ∪ B) V (x ∈ C}
=(A ∪ B) ∪ C olur. - A ∪ B = ∅ olduğunda A ve B kümeleri boş küme olur. Bu durumun tersi de doğrudur. Kümeler boş küme ise birleşim kümesi de boş küme olur. A ∪ B = ∅ ⇔ A = ∅ ve B = ∅ olur.
- B ⊂ A ⇒ A ∪ B = {x | x ∈ A V x ∈ B} = {x | x ∈ A V x ∈ A} = {x | x ∈ A } = A olduğundan B ⊂ A ⇒ A ∪ B = A olur.
Kümelerde Kesişim İşlemi
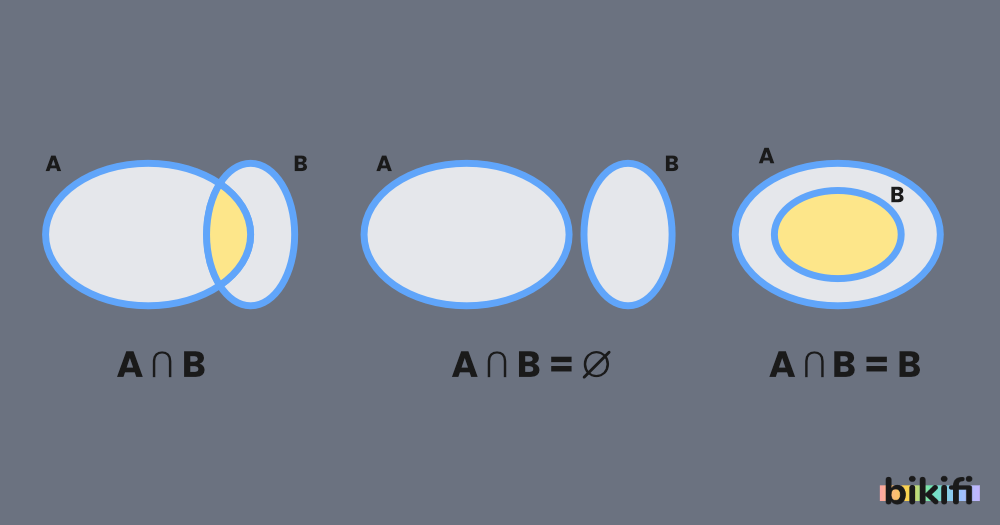
A ile B iki küme olsun, A ile B kümelerinin ortak elemanlarının alınması ile oluşan kümeye, A ve B kümelerinin kesişim kümesi adı verilir. A ∩ B şeklinde gösterilir.
A ∩ B = {x | x ∈ A ve x ∈ B} = {x | x ∈ A ∧ x ∈ B} olarak ifade edilir.
Mantıktaki ∧ (ve) sembolü kümelerde ∩ (kesişim) olarak ifade edilir.
Kesişim İşleminin Özellikleri
- Bir kümenin kendisi ile kesişimi yine kendisidir. Buna tek kuvvet özelliği denir. A ∩ A = { x | x ∈ A ∧ x ∈ A} = { x | x ∈ A} = A olduğundan A ∩ A = A olur.
- Kümelerde kesişim işleminin değişme özelliği vardır. A ∩ B = { x | x ∈ A ∧ x ∈ B} = { x | x ∈ B ∧ x ∈ A} = B ∩ A olduğundan A ∩ B = B ∩ A olur.
- Kümelerde kesişim işleminin birleşme özelliği vardır.
A ∩(B∩C) = {x| (x ∈ A) ∧ x ∈ (B∩C)} = {x| (x ∈ A) ∧ (x ∈ B ∧ x ∈ C)}
={x| (x ∈ A ∧ x ∈ B) ∧ (x ∈ C)} = {x| x ∈ (A∩B) ∧ (x ∈ C)}
=(A∩B) ∩ C olur. - Bir kümenin boş küme ile kesişimi boş kümedir. Bu durumda boş küme, kesişim işleminin yutan elemanıdır. A ∩ ∅ = {x| x ∈ A ∧ x ∈ ∅} = {x| x ∈ ∅} = ∅ olduğundan A ∈ ∅ = ∅ = A = ∅ olur.
A∩B = ∅ ⇒ A ve B kümelerinin ortak elemanı yoktur. Bu durumda A ve B kümeleri ayrık kümelerdir denir. - B ⊂ A ⇒ A ∩ B = {x| x ∈ A ∧ x ∈ B} = {x| x ∈ B} = B olduğundan B ⊂ A ⇒ A ∩ B = B olur. Bu durumda kesişim kümesi, kapsayan kümeye (alt kümeye) eşit olur.
- Kesişim işleminin birleşim işlemi üzerine hem soldan hem sağdan dağılma özelliği vardır. A ∩ (B∪C) = (A∪B) ∩ (A∪C) Kesişim işleminin birleşim işlemi üzerine dağılma özelliği vardır.
- Birleşim işleminin kesişim işlemi üzerine hem soldan hem sağdan dağılma özelliği vardır. A ∪ (B∩C) = (A∩B) ∪ (A∩C) Birleşim işleminin kesişim işlemi üzerine dağılma özelliği vardır.
- A ve B ayrık kümeler ise A∪ B kümesinin eleman sayısı, s(A∪B)=s(A)+s(B) şeklinde olur.
- A ve B ayrık kümeler değilse A∪ B kümesinin eleman sayısı, s(A∪B)= s(A) + s(B) – s(A∩B) olur. Burada çıkarılan değer kümelerin kesişimi sonucu toplama işlemine iki defa eklenen değerdir.
Evrensel Küme ve Bir Kümenin Tümleyeni
Belirli bir konuda üzerinde işlem yapılan, bütün kümeleri içine alan, boş küme olmayan en geniş kümeye evrensel küme denir. A ⊂ E olmak üzere, evrensel kümede olup A kümesinde olmayan elemanların kümesine, A kümesinin tümleyeni denir. A’ ile gösterilir.
A’= {x| x ∈ E ∧ x ∉ A} şeklinde ifade edilir.
- A ⊂ E ise s(E) = s(A)+ s(A’)
- (A’)’=A
- ∅’=E, E’=∅
- De Mogan Kuralları:
- (A ∪ B)’ =A’ ∩ B’
- (A ∩ B)’ = A’ ∪ B’
- A ⊂ B ⇒ B’ ⊂ A’
- A ∪ A’ = E, A ∩ A’ = ∅
- E ∪ A’= E, E ∩ A’ = A’
Kümelerde Fark İşlemi
A ve B iki kümedir. A kümesinde olup B kümesinde olmayan elemanların oluşturduğu kümeye (yalnız A da olan elemanların oluşturduğu kümeye) A fark B denir. A-B veya A\B şeklinde gösterilir.
A-B=A\B={x| x ∈ A ∧ x ∉ B} olur.
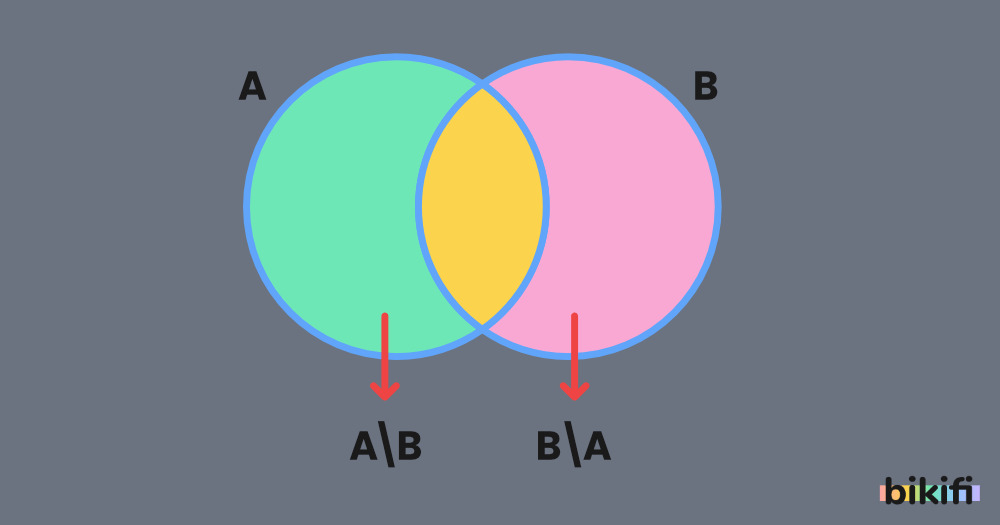
- A\B = {x| x ∈ A ∧ x ∉ B} = {x| x ∈ A ∧ x ∉ B’}=A∩B’ olduğundan A\B elde edilir.
- A\A=∅
- A\∅=A
- E\A=A’
- A\E=∅
- ∅\A=∅
- (A\B)’=(A∩B’)’=A’∪(B’)’=A’∪B
- A ⊂ B ⇒ A\B={x| x ∈ A ∧ x ∉ B} demektir. Ancak A ⊂ B durumunda x ∉ B olamaz. Sonuç olarak A ⊂ B ⇒ A\B= ∅ olur.
Küme İşlemleri ile Sembolik Mantık Kuralları Arasındaki İlişki
| Sembolik Mantık | 0 | 1 | v | ∧ | Değil(‘) | ≡ |
| Kümeler | ∅ | E | ∪ | ∩ | Tümleyen | = |
| Sembolik Mantık | Kümeler |
|---|---|
| p V p’ ≡ 1 | A ∪ A’ = E |
| p ∧ p’ ≡ 0 | A ∩ A’ = ∅ |
| p V 1 ≡ 1 | A ∪ E = E |
| p V p ≡ p (Tek kuvvet özelliği) | A ∪ A = A (Tek kuvvet özelliği) |
| p ∧ p ≡ p (Tek kuvvet özelliği) | A ∩ A = A (Tek kuvvet Özelliği) |
| p V q ≡ q V p (Değişme özelliği) | A ∪ B = B ∪ A (Değişme özelliği) |
| (p V q)’ ≡ p’ ∧ q’ (De Morgan Kuralı) | (A ∪ B)’ = A’ ∩ B’ (Tümleme özelliği) |
| p V (q ∧ r) ≡ (p V q) ∧ (p V r) (Dağılma özelliği) | A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C) (Dağılma Özelliği) |













