Örneğin; “Türkçemizdeki sesli (ünlü) harflerin kümesi” veya “10 dan küçük doğal sayıların kümesi” ifadeleri birer küme belirtir.
Kümeler genellikle A, B, C,… gibi büyük harflerle gösterilir. Bir x öğesi, bir A kümesinin elemanı ise bunu “x ∈ A” biçiminde gösterip “x elemanıdır A” diye okunur. Eğer x öğesi A kümesinin elemanı değilse “x ∉ A” biçiminde gösterilir, “x elemanı değildir A” şeklinde okunur. Kümede bir eleman sadece bir kez gösterilir.
Kümelerin Gösterimi
Liste Yöntemi İle Gösterim
Kümenin elemanlarının, sıra gözetmeksizin, { } biçimindeki küme parantezinin içine, aralarına virgül konularak yazılmasına kümenin liste yöntemiyle gösterilmesi denir.
Örneğin: A={0, 1, 2, 3} ve B={B,İ, K, F} kümeleri liste yöntemiyle yazılmış iki kümedir.
Venn Şeması Yöntemi ile Gösterim
Kapalı bir eğri içerisinde, kümenin elemanlarının önlerine nokta konularak yazılmasına, kümenin Venn Şeması ile gösterilmesi denir.
Örneğin: A={1, 2} kümesi Venn Şeması ile aşağıdaki gibi değişik şekillerde gösterilir.
Ortak Özellik Yöntemi İle Gösterim
Kümenin elemanları arasında ortak özellik varsa bu özelliğin belirtilerek kümenin ifade edilmesine, kümenin ortak özellik yöntemi ile gösterim denir.
A={ x | p(x) } biçiminde yazılır. Burada x| ifadesi x öyle ki diye okunur.
Boş Küme
Hiç elemanı olmayan kümeye boş küme denir. Boş kümenin gösterimi olup liste yöntemi ile gösterimi { } biçimindedir. Boş kümenin eleman sayısı sıfırdır.
Önemli: {} ve { { } } kümeleri, birer elemanlı kümeler olduğu için boş küme değildir.
Sonlu ve Sonsuz Kümeler
Eleman sayıları bir doğal sayı ile gösterilebilen kümelere sonlu küme, sonlu olmayan kümelere de sonsuz küme denir.
Alt Küme
Bir A kümesinde bulunan her eleman (A nın bütün elemanları) bir B kümesinin de elemanı ise, A kümesi B kümesinin alt kümesidir denir. A ⊂ B biçiminde gösterilir.
Bu ifade, B kümesi A kümesini kapsar şeklinde de söylenir. B A veya B A biçiminde gösterilir.
Alt kümenin Venn şemasıyla gösterilişi aşağıdaki gibidir.
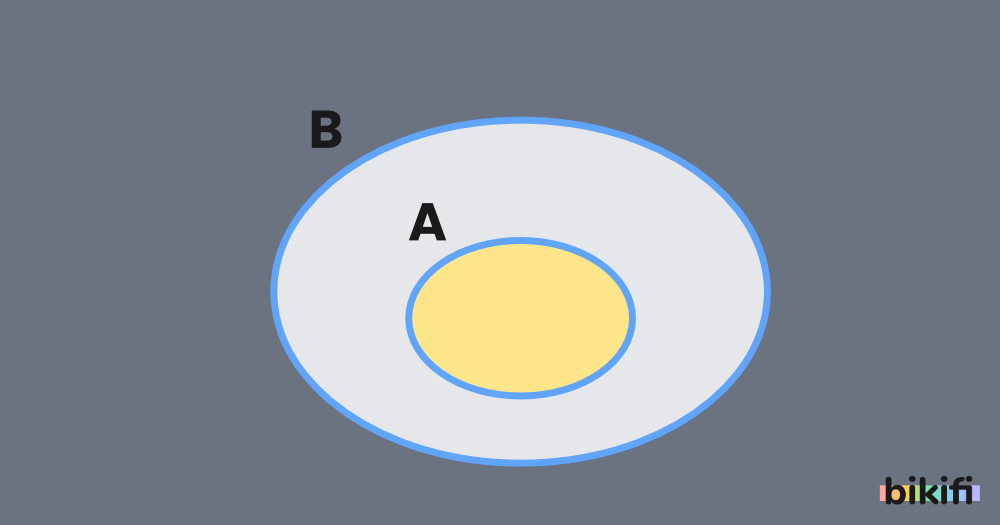
A kümesinin en az bir elemanı, B kümesinin elemanı değil ise A kümesi B kümesinin alt kümesi değildir denir ve A ⊄ B biçiminde gösterilir.
Alt Kümenin Özellikleri
- Her küme, kendisinin alt kümesidir. (A ⊂ A)
- Boş küme, her kümenin alt kümesidir. (∅ ⊂ A)
- (A ⊂ B) ∧ (B ⊂ C) ⇒ (A ⊂ C) dir.
- n elemanlı bir kümenin alt kümelerinin sayısı 2n şeklinde hesaplanır.
Öz Alt Küme
Bir kümenin kendisi dışındaki alt kümelerine öz alt küme denir.
Bir kümenin öz alt kümelerinin sayısı 2n-1 ile hesaplanır.
Eşit Küme
Aynı elemanlardan oluşan kümelere eşit kümeler denir. A ve B eşit iki küme ise A=B şeklinde gösterilir. Eğer bu kümeler eşit değilse bu durum A B şeklinde gösterilir.
A ve B kümelerinin birbirine eşit kümeler olması ancak ve ancak bu kümelerin birbirinin alt kümesi olmasıyla mümkündür. Bu durum (A ⊂ B) ∧ (B ⊂ A) ⇔ A = B şeklinde ifade edilir.














