Bir Doğru Parçasını Belli Bir Oranda Bölen Noktanın Koordinatları

Bir Doğru Parçasının Orta Noktasının Koordinatları

Analitik düzlemde bir doğru parçasının orta noktasını bulmak için iki ucunun koordinatlarına ihtiyacımız vardır. Orta noktanın x ve y değerleri doğru parçasının iki ucunun tam ortasında yer alacağı için bu iki ucun x ve y değerlerinin de tam ortasında yer alması gerekir.

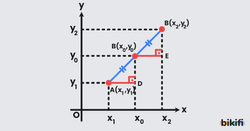
Yukarıda bulunan analitik düzlemdeki doğru parçası üzerinden devam edelim. Bir ucu A(x₁,y₁) ve diğer ucu B(x₂,y₂) olan AB doğru parçasının orta noktası C(x₀,y₀) olsun. Burada x₀ noktası x₁ ve x₂ noktasının tam ortasıdır. Bu nedenle x₀‘ın x₁ ve x₂‘ye olan uzaklıkları eşit olacaktır. Aynı işlemler y değerleri için de yapılır.

Normalde iki sayıyı toplayıp ikiye böldüğümüzde bu iki sayının ortasını bulabiliriz fakat burada basit bir matematikle orta noktayı bulmayı gördük. Sonuç olarak iki ucunun koordinatlarını verilen doğru parçasının orta noktasının koordinatları aşağıda gösterildiği gibidir.

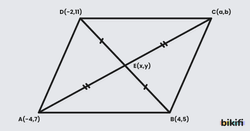
Örnek: Analitik düzlemde köşelerinin koordinatları A(-4,7), B(4,5), C(a,b) ve D(-2,11) olan ABCD paralel kenarında C noktasının koordinatlarını bulalım.

Çözüm: Bu sorunun çözümünde paralelkenarın köşegenlerini kullanacağız. Paralelkenarın köşegenleri birbirini iki eşit parçaya böler. Koordinatlarını bildiğimiz B ve D köşelerinin orta noktasını bulursak aynı zamanda A ve C noktasının da orta noktasını bulmuş oluruz. Orta noktasını ve bir ucunu kullanarak doğru parçasının diğer ucunu bulabiliriz.

İlk olarak B ve D noktasının orta noktası olan E(x,y) noktasının koordinatlarını bulalım.

Şimdi ise A ve C noktalarından E noktasını buluyormuşuz gibi aynı işlemleri yapalım fakat orta noktayı bildiğimiz için buraya bilinmeyen C noktasının koordinatlarına ulaşacağız.

Buna göre C noktasının koordinatları:

Bir Doğru Parçasını Belli Bir Oranda İçten Bölen Noktanın Koordinatları

Analitik düzlemde bir doğru parçası üzerindeki noktanın doğru parçasının uçlarına olan x ve y uzaklıklarıyla oluşan dik üçgenler arasındaki benzerlikleri kullanarak koordinatlarını bulabiliriz.

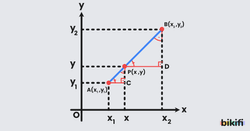
Yukarıda bulunan görseldeki gibi bir ucu A(x₁,y₁) ve diğer ucu B(x₂,y₂) olan AB doğru parçası üzerinde bir P(x,y) noktası seçmiş olalım. Bu noktalardan eksenlere dik çizgiler çekip uzantılarını birleştirdiğimizde açıları eşit dik üçgenler oluşacaktır. Açıları eşit olduğu için bu dik üçgenler benzer olacaktır ve bu benzer üçgenler arasında aşağıdaki gibi orantı kurabiliriz.

Bu durumda iki üçgen arasındaki benzerlik oranı k oldu. Şimdi k oranını kullanarak P noktasının x ve y koordinatlarını bulalım.

İlk olarak x değerlerini kullandığımız kenarlardan başlayalım.

Aynı işlemleri y değerini bulmak için yapacağız.

Böylelikle doğru parçasında üzerinde belirlediğimiz P noktasının koordinatlarını A ve B noktasının koordinatları cinsinden bulduk.

Not: Eğer k benzerlik oranı 1 olursa üçgenler eşit olacaktır ve P(x,y) noktası AB doğru parçasının orta noktası olur.

Bir Doğru Parçasını Belli Bir Oranda Dıştan Bölen Noktanın Koordinatları

Analitik düzlemde bir doğru parçasının üzerinde değil de uzantısında yer alan noktanın doğru parçasının uçlarına olan x ve y uzaklıklarıyla oluşan iç içe geçmiş dik üçgenler arasındaki benzerlikleri kullanarak koordinatlarını bulabiliriz.

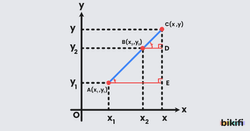
Yukarıda bulunan görseldeki gibi bir ucu A(x₁,y₁) ve diğer ucu B(x₂,y₂) olan AB doğru parçasının uzantısında(dışında) yer alan bir C(x,y) noktası seçmiş olalım. Burada da noktalardan eksenlere dik çizgiler çekip uzantılarını birleştirdiğimizde iç içe iki benzer dik üçgen elde ederiz. Bu iki üçgen arasındaki benzerliği kullanarak dışarıdaki C noktasının koordinatlarını bulabiliriz.

İlk olarak x değerlerini veren uzunluklar arasında benzerlik kurarak başlayalım.

Aynı şekilde y değerini bulalım.

Böylelikle belirlediğimiz AB doğru parçası dışında yer alan C noktasının koordinatlarını A ve B noktasının koordinatları cinsinden bulmuş olduk.

Not: Sorularda doğru parçasının dışında kalan nokta için yukarıda bulduğumuz bu eşitliği kullanabilirsiniz. Başka bir yol düşünecek olursak doğru parçasının dıştaki noktaya yakın olan ucunu doğru parçasını içten bölen noktaymış gibi düşünebiliriz. Yani AB doğru parçası ve dışında bulunan C noktası yerine AC doğru parçasının içinde bulunan B noktası gibi düşünüp işlemleri buna göre yapabiliriz. Böylelikle tek bir eşitlikle hem içten hem de dıştan bölen durumu çözebiliriz.

Bir Üçgenin Ağırlık Merkezinin Koordinatları

Analitik düzlemde bir üçgenin köşelerinin koordinatlarının ortalaması üçgenin ağırlık merkezini verir. Koordinatlarının ortalamasını alırken her köşenin x ve y değerlerini ayrı ayrı toplayıp ikisini de 3’e böldüğümüzde üçgenin ağırlık merkezinin x ve y değerlerini bulmuş oluruz.

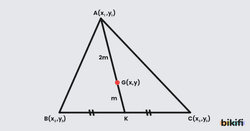
Bunun ispatını yapacak olursak bir ABC üçgenini ele alalım. A köşesinden BC kenarına bir kenarortay çiziliyor ve bu kenarortay ağırlık merkezinden geçer. Aynı zamanda ağırlık merkezi bu kenarortayı 2’ye 1 oranında böler.

İlk olarak K noktası B ve C noktalarının tam orta noktası olduğu için B ve C koordinatlarının toplamının yarısı K noktasını verecektir.

Şimdi AK doğru parçasına baktığımızda G ağırlık merkezi bu doğru parçasını içten bölen nokta olarak görünmektedir. G noktasının kenarlara olan uzaklıklarının oranını da bildiğimize göre içten bölen durumda kullandığımız eşitliği burada kullanabiliriz.

Böylece G ağırlık merkezinin koordinatlarını üçgenin köşeleri cinsinden

olarak buluruz.