Analitik Düzlem
Aynı düzlem üzerinde başlangıç noktalarından dik kesişen sayı doğrularından oluşan sisteme koordinat sistemi denir. Üzerinde bir koordinat sistemi bulunduran düzleme ise analitik düzlem denir.
Koordinat sistemdeki yatay sayı doğrusuna x ekseni veya apsis ekseni, dikey sayı doğrusuna ise y ekseni veya ordinat ekseni denir. x ve y ekseninin kesiştiği noktaya başlangıç noktası veya orijin denir ve O(0,0) şeklinde gösterilir.
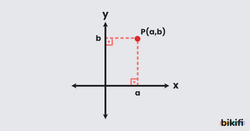
Analitik düzlemde noktaların koordinatları sayı ikilileri şeklinde verilir. Bu sayılar belirlenen noktadan her iki eksene de dik çizildiğinde eksen üzerinde denk geldiği sayılardır. Bir noktadan x eksenine çizilen dikme sonucu kestiği sayı bu noktanın apsisidir ve noktanın koordinatlarında sola yazılır. Aynı noktadan y eksenine çizilen dikmede ise kestiği sayı noktanın ordinatı olur ve bu noktanın koordinatlarında sağ tarafa yazılır.
Yukarıda analitik düzlemde verilen P noktasından eksenlere çizilen dikmelerin kestiği noktalar görüldüğü gibi yanına ikili şekilde yazılarak koordinatları belirtilmiştir.
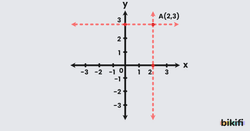
Koordinatları verilen bir noktayı analitik düzlemde göstermek istersek verilen sayı ikililerini eksenlerine koyup bu noktalardan eksenlere dik doğrular çizeriz ve bu doğruların kesiştiği nokta bizim koordinatları verilen noktamızdır.
Yukarıda örnek olarak A(2,3) noktası verilmiştir. A noktasının apsisi 2 olduğu için x ekseninde 2 noktasından ekseni dik kesen bir doğru çizilir. Aynı şekilde A noktasının ordinatı 3 olduğu için y ekseninde 3 noktasından eksene dik doğru çizilir. Son olarak bu doğruların kesiştiği yere baktığımızda burası A noktası olacaktır.
Analitik Düzlemde Bölgeler
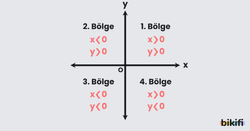
Koordinat sistemi, analitik düzlemi 4 bölgeye ayırır. Bu bölgeler iki eksenin de pozitif olduğu sağ üst taraftan başlayarak saat yönünün tersine doğru devam eder.
- 1. Bölgede bulunan bir noktanın her iki eksen değeri de pozitiftir. (+,+)
- 2. Bölgede bulunan bir noktanın x eksenindeki değeri negatif, y eksenindeki değeri ise pozitiftir.(-,+)
- 3. Bölgede bulunan bir noktanın her iki eksen değeri de negatiftir.(-,-)
- 4. Bölgede bulunan bir noktanın x eksenindeki değeri pozitif, y eksenindeki değeri ise negatiftir.(+,-)
Not: Eksenler üzerinde bulunan noktalar hiçbir bölgeye dahil değildir.
Örnek: A(-1,m-4) ve B(2-n,3) noktaları analitik düzlemin aynı bölgesinde bulunduğuna göre m+n toplamının değer aralığını bulalım.
Öncelikle bu noktalar aynı bölgede bulunduğuna göre x ve y değerlerinin işaretleri aynı olacaktır. A noktasına baktığımızda x eksenindeki değer negatif, böylece B noktası aynı bölgede olduğu için onun da x eksenindeki değer negatif olacaktır. B noktasının ise y eksenindeki değer pozitiftir, yine aynı bölgede bulunduklarından A noktasının da y eksenindeki değer pozitif olacaktır. A ve B noktalarının işaretlerine baktığımızda bu noktalar 2. bölgede bulunmaktadır.
A noktasının y eksenindeki değer pozitif olduğu için m-4 değeri sıfırdan büyük olacaktır. Böylelikle m’nin değerini 4’ten büyük buluruz.
B noktasının x eksenindeki değer negatif olduğu için 2-n değeri sıfırdan küçük olacaktır. Buna göre n’nin değerini 2’den büyük buluruz.
Sonuç olarak m sayısı 4’ten ve n sayısı 2’den büyük olduğu için bu iki sayının toplamı 6’dan büyük olacaktır.
İki Nokta Arasındaki Uzaklık
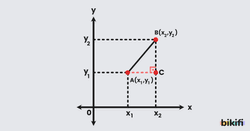
Analitik düzlemde verilen iki noktanın arasındaki uzaklığı kolaylıkla bulabiliriz. Analitik düzlemde verilen A(x1,y1) ve B(x2,y2) noktaları için ilk olarak her iki noktadan da eksenlere dik çizeriz. İki noktayı da birleştirdiğimizde eksenlere çizdiğimiz diklerle birlikte ortada bir dik üçgen(ABC) oluşacaktır. Bu dik üçgenin dik kenar uzunlukları eksenlerde kestiğimiz değerlerin farkına eşit olacaktır. Bu dik kenarların uzunluklarını bulduktan sonra Pisagor teoremiyle hipotenüs uzunluğunu bularak iki nokta arasındaki uzaklığa ulaşmış oluruz.
ABC üçgeninde Pisagor teoremi uyguladığımızda
Buna göre iki nokta arasındaki uzaklık ise aşağıdaki gibi olur.
Örnek: M(3,-4) ve N(-2,8) noktaları arasındaki uzaklığı bulalım.
İlk olarak x değerlerinin kendi arasındaki ve y değerlerinin kendi arasındaki farkları bulalım.
Bu değerler bir dik üçgenin dik kenar uzunlarıdır ve pisagor teoreminde bu kenarları kullanarak hipotenüsü yani iki noktanın arasındaki uzaklığı bulacağız.
Örnek: A(2,5), B(-4,1) ve C(0,m) olsun. Bu durumda |AB|=|BC| olduğuna göre m sayısının alabileceği değerleri bulalım.
|AB| ve |BC| uzunlukları eşit olduğuna göre her ikisi için de iki nokta arasındaki uzaklık bulma yöntemimizi kullanırız ve birbirine eşitleyerek sonuca ulaşabiliriz.
Bulduğumuz bu iki ifadeyi birbirine eşitleyelim.