Analitik Düzlemde Doğrunun Denklemi

Bikifi Instagram'da

Doğru Denklemi Yazma

Doğru denklemi çeşitli yöntemlerle yazılabilir. Soru çözümlerinde aşağıdaki yöntemlerden birisi seçilerek doğru denklemi yazılabilir.

Eğimi ve Bir Noktası Verilen Doğrunun Denklemi

Eğimini bildiğimiz bir doğrunun şeklini tahmin edebiliriz fakat analitik düzlemin neresinde yer aldığını bilemeyiz. Bize bu doğrunun geçtiği bir nokta verilirse o noktadan ve geçen ve belli eğimde sadece bir doğru olacağından bu doğrunun tam olarak nereden ve nasıl geçtiğini bulabiliriz. Kısacası, eğimi ve üzerindeki bir noktanın koordinatı bilinen doğruyu tam olarak çizebiliriz.

Bir d doğrusu A(x₁,y₁) noktasından m eğimiyle geçiyor olsun. Bu d doğrusu üzerine bir B(x,y) noktası olduğunu düşünelim. Bu doğrunun eğimini A ve B noktasını kullanarak bulabiliriz.

Aslında bir doğrunun denklemini bulurken her seferinde bunu uygulamamıza gerek yoktur. Kısa yoldan doğrunun bildiğimiz noktasının değerlerini x ve y’den çıkartıp eşitliğin iki tarafına yazarız ve x’in olduğu tarafı eğimle çarparak doğrunun denklemini elde edebiliriz. Daha sonra y’nin yanındaki değeri karşıya atarak y’yi yalnız bırakabiliriz.

şeklinde bir denklem elde ederiz.

İki Noktası Verilen Doğrunun Denklemi

İki noktası verilen doğrunun denklemini üçüncü bir (x,y) noktası düşünerek iki farklı şekilde eğim hesabı yaparak eşitlik yazarız ve bir denklem elde edebiliriz.

Bir d doğrusu A(x₁,y₁) ve B(x₂,y₂) noktalarından geçiyor olsun. Bu doğrunun denklemini yazarken C(x,y) noktasından geçtiğini düşünerek hem A ve B arasında eğim hesaplayarak hem de bu iki noktadan birinin C ile olan eğimini hesaplayarak aynı doğru üzerinde oldukları için bu iki eğimin eşit olduğunu biliriz.

İkinci bir yol olarak verilen iki noktadan eğimi hesaplayabilir ve bu eğimle iki noktadan birini kullanarak eğimi ve bir noktası verilen doğrunun denklemini yazabiliriz.

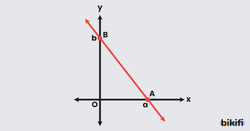
Bir doğrunun bilinen iki noktası A(a,0) ve B(0,b) gibi eksenleri kesen noktalarsa direkt x’i x eksenini kesen değere, y’yi y eksenin kesen değere bölüp topladığımızda her zaman 1’e eşit olur.

Eksenlere Paralel Doğruların Denklemi

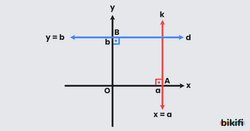
Eksenlere paralel doğrular hep aynı x veya y değerlerine sahip oldukları için x=a ve y=b gibi denklemleri olur.

Görseldeki d doğrusu için konuşursak x değeri ne olursa olsun y değeri her zaman b olacaktır. Bu nedenle y=b şeklinde denklem yazılır ve x ile ilgili bir şey yazmaz. Yani y değerinin b olduğunu kabul ettikten sonra x değerlerinin herhangi bir değer alabileceğini söylüyor.

Aynı şekilde k doğrusu için de tek bir x değeri olduğu ve yanına herhangi bir y değeri gelebileceğini biliriz. Bu nedenle k doğrusunun denklemi x=a olur.

Bir doğru x eksenine paralelse y eksenini bir noktada keser ve hep aynı y değerine sahip olacağı için y=b gibi bir denkleme sahip olur. y eksenine paralel bir doğru için de x=a denklemini yazarız. Yani doğrunun paralel olduğu eksenle denklemini yazdığımız eksen arasında bir ters ilişki vardır.

Orijinden Geçen Doğruların Denklemi

Orijinden geçen doğrular için eğimini ve bir noktasını bildiğimiz doğrular gibi denklemini buluruz. Eğimi m olarak verilen bir doğrunun orijinden geçtiğini biliyorsak, bu doğru üzerinde bir A(x,y) noktası olduğunu düşünerek eğim hesabı yapabiliriz.

Sonuç olarak eğimi ve orijinden geçtiği bilinen bir doğrunun denklemini yazarken eğimi x ile çarpıp y’ye eşitlememiz yeterlidir.

Denklemi Bilinen Doğruların Eğimi

Doğruların denklemlerini istediğimiz şekilde yazabiliriz fakat belli yazım kalıpları mevcuttur. Örnek olarak şeklinde yazdığımız denkleme doğrunun kapalı denklemi denir. Diğer bir şekli ise y’yi denklemin bir tarafında yalnız ve kat sayısı 1 olacak şekilde bıraktığımız denklemlerdir. şeklinde yazdığımız denklemlere doğrunun açık denklemi denir.

Doğrunun açık denkleminde her zaman x’in kat sayısı bize doğrunun eğimini verir. Burada dikkat edilmesi gereken unsur y denklemin bir tarafında yalnız ve kat sayısı 1 olacak. y’nin 1’den başka kat sayısı olduğu an eğim değişir.

İki Doğrunun Birbirine Göre Durumları

İki doğrunun birine göre 3 farklı durumda bulunabilir. Bunlar çakışık, paralel ve bir noktada kesişendir. Şimdi bu durumları aşağıdaki iki doğru denklemine göre tek tek inceleyelim.

Çakışık Denklemler

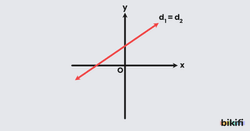
Doğru denklemlerinin bütün katsayıları arasındaki orantı eşit olan denklemler çakışık denklemlerdir.

Katsayıları arasında belli orantıya sahip denklemler aynı eğime sahip olur ve aynı noktalardan geçer. Böylece üst üste denk gelme durumu olur ve bu duruma denklemlerin çakışık olması denir. Bu doğruların denklemlerinden oluşan denklem sisteminin çözüm kümesi boş kümedir.

Paralel Doğrular

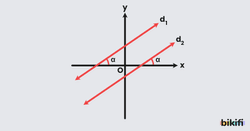
Doğru denklemlerinde x ve y’lerin kat sayıları arasındaki orantı eşit fakat sabit değerler arasında aynı orantı yoksa bu doğrular sadece paraleldir.

Denklemlerindeki x ve y’nin kat sayıları orantılı olan doğruların eğimleri eşit olur. Denklemin sabit ifadesi ise doğrunun tam konumunu bize verdiği için doğrular farklı konumlarda olur fakat paralel doğrular olurlar. Bu doğruların denklemlerinden oluşan denklem sisteminin çözüm kümesi boş kümedir.

Bir Noktada Kesişen Doğrular

Doğru denklemlerinde x ve y’lerin kat sayıları arasında belli bir orantı olmayan doğrulara bir noktada kesişen doğrular denir.

Denklemlerindeki x ve y’nin kat sayıları arasında orantı olmayan doğruların eğimleri farklıdır ve mutlaka bir noktada kesişirler. Bu doğruların denklemlerinden oluşan denklem sisteminin çözüm kümesi bize bir nokta verir. Bu nokta iki doğrunun kesiştiği noktadır.

Bu çözümlemeyi genellikle denklemleri alt alta yazıp x veya y’den birinin kat sayısını eşitleyecek şekilde denklemleri genişleterek birbirini götürüp diğer eksen değerini bulabiliriz. Bulduğumuz bu değeri de bir denklemde yerine yazarak diğer eksen değerini buluruz.