Mantığa Giriş: Önerme
Ders Notuna git →
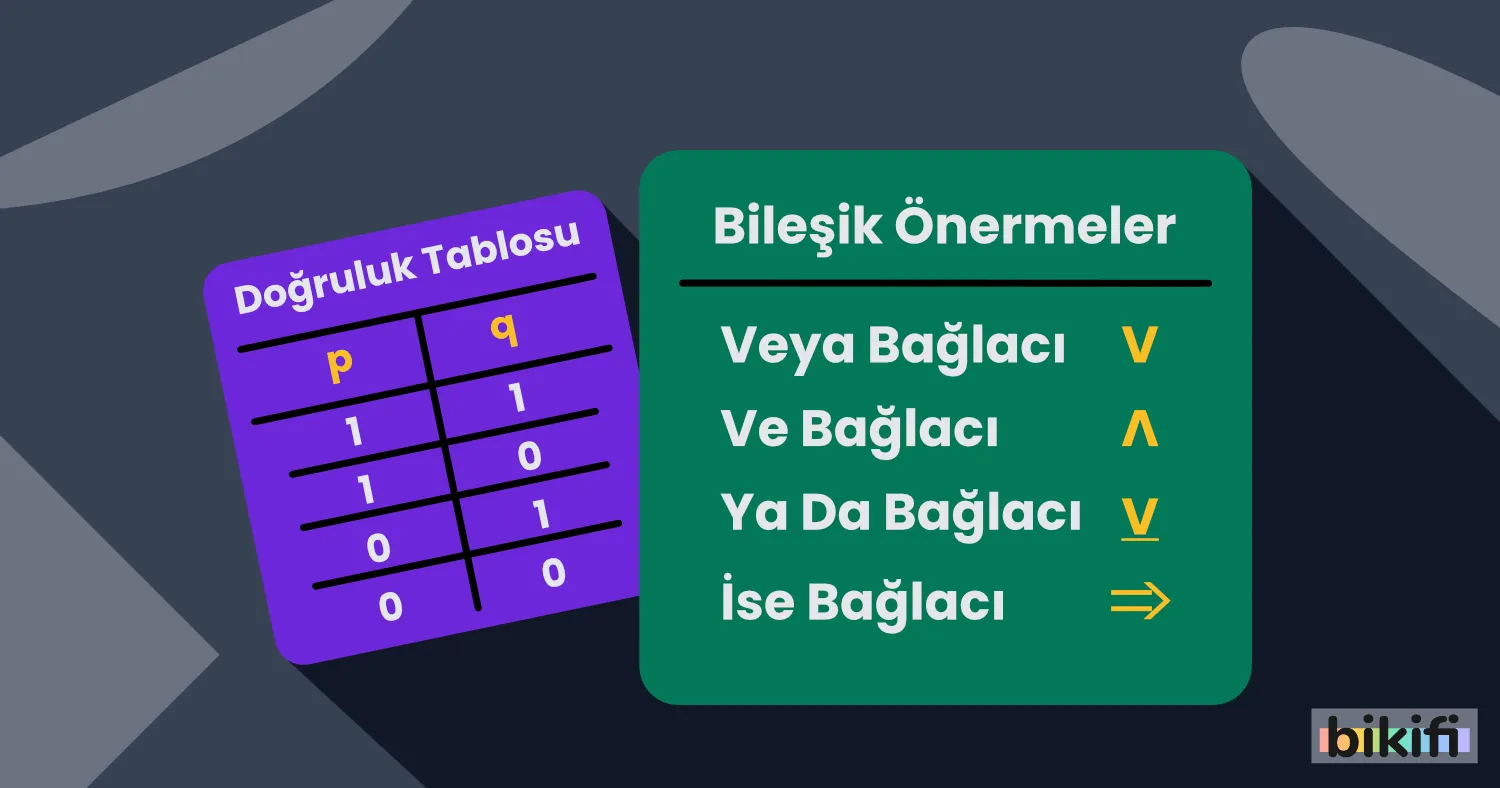
Bileşik Önerme
Ders Notuna git →
Koşullu Önerme
Ders Notuna git →
Güncel
Önermelerin Birbirine Dönüştürülmesi
Ders Notuna git →
Açık Önermeler ve İspat Kavramı
Ders Notuna git →
✍ PDF Çalışma Kaynakları
📘 Kurum: MEB – OGM Materyal
🔗 İndirme Linki: PDF Linki
📝 Ünite Kazanımları
- 9.1.1.1. Önerme, önermenin doğruluk değeri, iki önermenin denkliğini ve önermenin değilini açıklar.
- Boole ve Leibniz’in çalışmalarına yer verilir.
- 9.1.1.2. Bileşik önermeyi örneklerle açıklar, “ve, veya, ya da” bağlaçları ile kurulan bileşik önermelerin özelliklerini ve De Morgan kurallarını doğruluk tablosu kullanarak gösterir.
- 9.1.1.3. Koşullu önermeyi ve iki yönlü koşullu önermeyi açıklar.
- a) Koşullu önermenin karşıtı, tersi, karşıt tersi verilir.
- b) p ⇒ q ⇔ p′ ∨ q olduğu doğruluk tablosu yardımıyla gösterilir.
- c) “ve, veya, ya da, ise” bağlaçları kullanılarak verilen, en fazla üç önerme içeren ve en fazla dört bileşenli bileşik önermelere denk basit önermeler buldurulur.
- d) p ⇒ q ⇔ q ⇒ p ve (p ⇒ q) ∧ (q ⇒ p) ↔ (p ⇔ q) olduğu doğruluk tablosu ile gösterilir.
- 9.1.1.4. Her (∀) ve bazı (∃) niceleyicilerini örneklerle açıklar.
- Sözel olarak verilen ve niceleyici içeren açık önermeler, sembolik mantık diliyle; sembolik mantık diliyle verilen ve niceleyici içeren açık önermeler de sözel olarak ifade edilir.
- 9.1.1.5. Tanım, aksiyom, teorem ve ispat kavramlarını açıklar.
- Bir teoremin hipotezi ve hükmü belirtilir.
