Üçgen, geometrinin temel şekillerinden biridir ve alan hesaplaması matematikte sıkça karşılaştığımız bir konudur. Günlük hayatta arazi ölçümünden, mimari tasarıma, mühendislikten sanata kadar pek çok alanda üçgen alan hesaplamalarını kullanırız. Bu derste, üçgende alan hesaplamanın farklı yöntemlerini ve bu yöntemlerin pratik uygulamalarını öğreneceğiz.
Üçgenlerde Temel Alan Bağıntısı
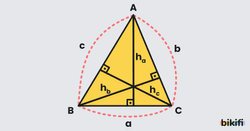
Bir üçgensel bölgenin alanı, bir kenar uzunluğu ile o kenar uzunluğuna ait yüksekliğin uzunluğunun çarpımının yarısına eşittir. A, B, C köşelerinden oluşan üçgensel bölgenin alanı biçiminde gösterilir.
Dar Açılı Üçgende Alan
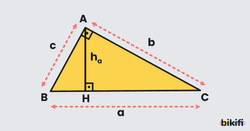
Dik Üçgende Alan
Dik üçgensel bölgenin alanı, dik kenar uzunluklarının çarpımının yarısının alınması ile bulunur. Eğer hipotenüse ait yükseklik biliniyorsa taban ile yükseklik çarpımının yarısı da alınabilir.
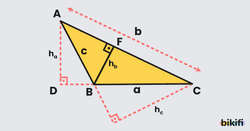
Geniş Açılı Üçgende Alan
Geniş açılı üçgenlerde [AB] ve[BC] kenarlarına ait yükseklikler üçgenin dış bölgesindedir.
Üçgenin Alan Hesaplama Yöntemleri
Üçgenin alanını hesaplamak için farklı durumlar ve veriler doğrultusunda çeşitli yöntemler kullanırız. Her yöntemin kendine özgü avantajları vardır ve hangi bilgilere sahip olduğumuza göre en uygun olanı seçeriz.
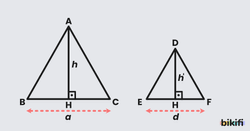
Yükseklikleri Eşit Olan Üçgenler
İki üçgenin yükseklikleri eşit olduğunda, bu üçgenlerin alanları arasında özel bir ilişki ortaya çıkar. Yükseklik (tabana dik olarak inen doğru parçası), üçgenin alanını hesaplamada kritik bir rol oynar.
Yükseklikleri eşit olan iki üçgen düşünelim. Bu durumda şu temel ilke geçerlidir:
Bu formül bize şunu söyler: Yükseklikleri aynı olan üçgenlerin alanlarının oranı, tabanlarının oranına eşittir. Örneğin, birinci üçgenin tabanı ikinci üçgenin tabanının 2 katıysa, birinci üçgenin alanı da ikinci üçgenin alanının 2 katı olacaktır.
Tabanları Eşit Olan Üçgenler
Şimdi de tabanları eşit olan üçgenleri inceleyelim. İki üçgenin tabanları aynı uzunlukta olduğunda, alanları arasındaki ilişki yüksekliklere bağlıdır:
Burada ve sırasıyla birinci ve ikinci üçgenin yükseklikleridir. Tabanlar eşit olduğu için, yükseklik ne kadar fazlaysa alan da o kadar büyük olur.
Paralel Doğrular Arasındaki Üçgenler
Paralel doğrular (aynı düzlemde olup hiçbir noktada kesişmeyen doğrular) arasında yer alan üçgenler, geometride çok ilginç özellikler gösterir. Bu özellikler, alan hesaplamalarını kolaylaştırır ve pratik problemlerin çözümünde bize yardımcı olur.
Ortak Tabanlı Üçgenler
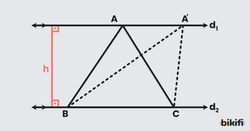
İki paralel doğru arasında, aynı tabana sahip üçgenler çizdiğimizi düşünelim. Ortak taban (iki üçgenin paylaştığı kenar), bu üçgenlerin alt kenarı olsun. Üçgenlerin tepeleri de üstteki paralel doğru üzerinde farklı noktalarda bulunsun.
Temel Teorem: Paralel doğrular arasında ortak tabanlı tüm üçgenlerin alanları birbirine eşittir.
Bunun nedeni şudur: Paralel doğrular arasındaki dik uzaklık her noktada aynıdır. Bu uzaklık, ortak tabanlı tüm üçgenlerin yüksekliği olur. Taban ve yükseklik aynı olduğu için, alanlar da eşit olur.
Ortak Olmayan Bölgeler
İki üçgen kesiştiğinde, ortak ve ortak olmayan bölgeler oluşur. Paralel doğrular arasındaki üçgenlerde özel bir durum ortaya çıkar:
Alan Eşitliği Teoremi: Paralel doğrular arasında ortak tabanlı iki üçgenin ortak olmayan bölgelerinin alanları birbirine eşittir.
Bu teorem, karmaşık görünen problemleri çok basitleştirir. İki üçgen kesiştiğinde dört bölge oluşur: sadece birinci üçgende olan bölge, sadece ikinci üçgende olan bölge, her ikisinde de olan ortak bölge ve hiçbirinde olmayan bölge. Teorem bize, sadece birinci üçgende olan bölgenin alanının, sadece ikinci üçgende olan bölgenin alanına eşit olduğunu söyler.
Benzer Üçgenler ve Alan
Benzer üçgenler (açıları eşit, kenarları orantılı olan üçgenler), geometride sıkça karşılaştığımız özel üçgenlerdir. İki üçgen benzer olduğunda, alanları arasında özel bir ilişki vardır.
Benzerlik Oranı İle Alan İlişkisi
Benzerlik oranı (karşılıklı kenarların oranı), benzer üçgenlerde harfiyle gösterilir. Örneğin, büyük üçgenin her kenarı, küçük üçgenin karşılık gelen kenarının 3 katıysa, benzerlik oranı ‘tür.
Temel Kural: Benzer üçgenlerin alanlarının oranı, benzerlik oranının karesine eşittir.
Bu formül çok önemlidir. Kenarlar 2 kat büyürse, alan 4 kat büyür. Kenarlar 3 kat büyürse, alan 9 kat büyür. Bunun nedeni, alanın iki boyutlu olmasıdır; hem genişlik hem yükseklik aynı oranda büyür.
Trigonometrik Alan Formülü
Bazen üçgenin iki kenarını ve bu kenarlar arasındaki açıyı biliriz, ancak yüksekliği bilmeyiz. Bu durumda trigonometrik alan formülü devreye girer.
İki Kenar ve Aralarındaki Açı
Üçgenin iki kenarı ve , aralarındaki açı olsun. Alan formülü:
Bu formül, sinüs (bir açının karşı kenarının hipotenüse oranı) fonksiyonunu kullanır. Açı 90 derece olduğunda olur ve formül bildiğimiz dik üçgen alan formülüne dönüşür.
📚 Konuyla İlgili Terimler Özeti
- Üçgen alanı (⭐⭐⭐): Üçgenin kapladığı yüzey ölçüsüdür. Temel formülü (taban × yükseklik) ÷ 2 şeklindedir. Günlük hayatta arazi ölçümünden, kumaş hesaplamalarına kadar geniş kullanım alanı vardır.
- Benzerlik oranı (⭐⭐⭐): Benzer üçgenlerde karşılıklı kenarların birbirine oranıdır ve harfiyle gösterilir. Örneğin, bir üçgenin her kenarı diğerinin 3 katıysa, benzerlik oranı k=3’tür. Harita ölçeklendirme ve mimari planlarda yaygın olarak kullanılır.
- Paralel doğrular (⭐⭐): Aynı düzlemde bulunup hiçbir noktada kesişmeyen doğrulardır. Tren rayları paralel doğrulara güzel bir örnektir.
- Ortak taban (⭐⭐): İki üçgenin paylaştığı kenardır. Bu kenar her iki üçgen için de taban görevi görür.
- Yükseklik (⭐⭐): Üçgenin bir köşesinden karşı kenara (tabana) dik olarak inen doğru parçasının uzunluğudur. Üçgenin alanını hesaplamada kullanılır.
- Benzer üçgenler (⭐): Açıları eşit, kenarları orantılı olan üçgenlerdir. Tüm eşkenar üçgenler birbirine benzerdir.
- Trigonometrik alan (⭐): İki kenar ve aralarındaki açı bilindiğinde, sinüs fonksiyonu kullanılarak hesaplanan alan formülüdür.