sinx=a, cosx=a ve tanx=a Biçimindeki Trigonometrik Denklemler
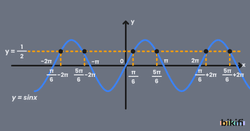
sinx=a Denklem Çözüm Kümesi
Sinüs fonksiyonunda bir açının kendisiyle bu açının π açısından çıkartılmış hali aynı sonucu vermektedir. Aynı zamanda sinüsün periyodu 2π olduğu için bu açılara 2π eklediğimizde sonuç değişmeyecektir. sinx=a denkleminde köklerden birini olarak aldığımızda denklemin çözüm kümesi aşağıdaki gibi olacaktır.
Örnek olarak durumunda açısının alabileceği değerler aşağıdaki sinüs grafiğinde verilmiştir.
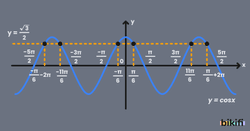
cosx=a Denklem Çözüm Kümesi
Kosinüs fonksiyonunda bir açının kendisiyle bu açının negatif işaretli hali aynı sonucu vermektedir. Sinüs fonksiyonu gibi kosinüste de periyodumuz 2π olduğu için her 2π de bir sonuç tekrar edecek. cosx=a denkleminde köklerden birini olarak aldığımızda denklemin çözüm kümesi aşağıdaki gibi olacaktır.
Örnek olarak durumunda açısının alabileceği değerler aşağıdaki kosinüs grafiğinde verilmiştir.
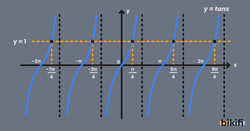
tanx=a Denklem Çözüm Kümesi
Tanjant fonksiyonunun periyodu π olduğu için bir açıya her π açısını ekleyip veya çıkarttığımızda aynı sonucu alacağız. tanx=a denkleminde köklerden birini olarak aldığımızda denklemin çözüm kümesi aşağıdaki gibi olacaktır. Tanjantta geçerli olan her şey kotanjant için de geçerlidir.
Örnek olarak durumunda açısının alabileceği değerler aşağıdaki tanjant grafiğinde verilmiştir.
sinf(x)=a, cosf(x)=a ve tanf(x)=a Biçimindeki Trigonometrik Denklemler
Trigonometrik denklemlerde çözüm kümesini bulmak istediğimizde trigonometrik fonksiyonu tek başına kalacak şekilde düzenleriz. Trigonometrik fonksiyonun açısı her zaman bir açı olmayabilir. Bu açılar da denklem şeklinde verilebilir ve denklemin eşit olabileceği her sonuca eşitleyerek denklemi çözmek gerekir.
Örnek olarak sinüs fonksiyonu üzerinden bir örnek vermek istersek denklemi için önce sinüsü yalnız bırakırız ve karşıdaki değere göre sinüsün alacağı açıları bularak sinüsün içinde yazan değere eşitleyerek çözebiliriz.
Burada karşımıza iki seçenek çıkmaktadır. İlk olarak sonucunu sinüste açısı ile üzerine 2π ve katlarını eklediğimizde bulabiliriz. Diğer bir durum ise açısını π açısından çıkartarak sinüste yine aynı sonucu veren diğer açıyı buluruz. Böylelikle açısı ile üzerine 2π ve katlarını eklediğimiz durumları da alabiliriz. Sonuç olarak sinüsün içerisindeki açısını bulduğumuz bu iki durumdaki açılara eşitleyerek açısının alabileceği tüm değerleri yani çözüm kümesini bulabiliriz.
veya
Çözüm kümesi
Trigonometrik Denklemlerin Çarpanlarına Ayırarak Çözümü
Trigonometrik denklemlerde ortak olan bir trigonometrik ifadeyi onun parantezine alarak alabileceği değerlere bakabiliriz, yalnız bırakabiliriz veya üslü bir ifade varsa bir harf tanımlayarak denklemi çözerek sonuçları trigonometrik ifadeye eşitleyebiliriz. Aşağıda bu durumla ilgili örneğimizi inceleyelim.
trigonometrik denklemi çözmek istersek gördüğümüz yerlere x koyarak denklemi çözeriz ve x bilinmeyeninin alabileceği değerleri ile eşitleyerek mümkün olan çözüm kümesine ulaşabiliriz.
Sinüs [-1,1] aralığında bir değer aldığı için 2’ye eşit olamaz bu yüzden ilk çözüm kümemiz boş oldu. Diğer tarafta sinüsün ‘ye eşit olduğu değerler çözüm kümemiz olacaktır.
Trigonometrik Özdeşlikler Yardımı İle Çözülebilen Denklemler
Bazı trigonometrik denklemlerde trigonometrik ifadelerin açıları her zaman eşit olmayabilir. Trigonometrik ifadeleri bir başka ifadeye çevirebilmek veya sadeleştirmeler yapabilmek için açılarının eşit olması gerekir. Açılarının eşit olmadığı denklemlerde toplam-fark ve yarım açı formüllerinden yararlanabiliriz. Aşağıda bu durumla ilgili örneğimizi inceleyelim.
Denkleminin [0,2π) aralığındaki çözüm kümesini bulalım.
Öncelikle paydaları eşitleyelim.
Pay kısmını incelediğimizde bunun bir sinüs fark formülünün açılımı olduğunu görüyoruz. Payı fark formülüne göre toparlayıp yarım açı formülüyle açarsak, paydayı da yine yarım açı formülüyle açısını iki katına çıkartırsak pay ve paydanın açısını da eşitleyebiliriz.
Gerekli sadeleştirmeleri yapınca açısının π ve katları şeklinde gittiğini görüyoruz. Bizim belirlediğimiz [0,2π) aralığı için köklerini bulup çözüm kümesini yazalım.
sinf(x)=sing(x) Denkleminin Çözüm Kümesi
Aynı bilinmeyene sahip iki farklı fonksiyonun sinüsü birbirine eşit olduğunda bir fonksiyonu bilinmeyen diğer fonksiyonu da direkt bir açı değeri gibi düşünerek sinx=a gibi bir denklem oluşturacağız.
Bildiğimiz üzere bir açı ve bu açının π’den çıkartılmış hali sinüste aynı sonucu vermektedir. Aynı bu mantıkla bir fonksiyon diğer fonksiyonun üzerine eklenmiş haline eşit olabilirken aynı zamanda bir fonksiyon diğer fonksiyonun π’den çıkartılmış halinin üzerine eklenmiş şekline eşit olabilir. Bunu bir örnekle pekiştirelim.
denklemini çözelim.
1. Eşitlik
2. Eşitlik
Burada iki farklı çözüm kümesi bulduk. Bunları tek bir çözüm kümesinde birleştirelim.
cosf(x)=cosg(x) Denkleminin Çözüm Kümesi
Aynı sinüste olduğu gibi fonksiyonların kosinüsü birbirine eşit olduğunda fonksiyonları eşitleriz ve bir tarafa ekleriz. Fakat kosinüste sinüsten farklı olan bir açının negatifi kosinüste aynı sonucu verir. Bu nedenle bir fonksiyonu diğerine eşitlerken aynı zamanda negatifine de eşitleyebiliriz.
Örnek olarak denkleminin aralığındaki çözüm kümesini bulalım.
1. Eşitlik
2. Eşitlik
İki farklı denklemden 4 farklı değer bulduk. Bunları bir çözüm kümesinde toplayalım.
tanf(x)=tang(x) veya cotf(x)=cotg(x) Denkleminin Çözüm Kümesi
Tanjant ve kotanjant eşitlikleri için yine denklemde iki fonksiyon karşılıklı yazılır ve fonksiyonlardan sadece birine k.π eklenerek eşitlik sağlanır.
Örnek olarak denkleminin çözüm kümesini bulalım.
Çözüm kümesini rahat bir şekilde bulduk.
a.sinf(x)+b.cosf(x)=c Biçimindeki Denklemlerin Çözüm Kümesi
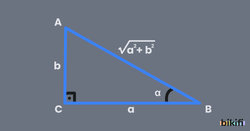
Bu denklemlere (a, b, c sayıları sıfırdan farklı olması şartıyla) sinf(x) ve cosf(x)’e göre lineer(doğrusal) denklemler denir. Bu tür denklemleri bir dik üçgene uyarlayarak açıklayalım.
Buraya kadar açıklamak gerekirse bize verilen denklemdeki sinüs ve kosinüsün kat sayılarının bir dik üçgenin dik kenarları olduğunu varsaydığımız bir olasılığı canlandırdık ve gerekli sadeleştirmeleri yaptığımızda son bulduğumuz denkleme kadar indirgedik. Bu aşamada ise bir sinüslü ifadenin [-1,1] aralığında olduğunu biliyoruz ve bunu ifadesiyle çarparsak c sayısının alabileceği değer aralığını buluruz.
Tarafların kareleri alınırsa
Sonuç kısmına geldiğimizde bulduğumuz bu eşitsizlik bu tür denklemleri çözebilmemiz için ön şart olacaktır. a.sinf(x)+b.cosf(x)=c biçimindeki denklemleri çözerken eğer yukarıdaki şart sağlanıyorsa her terimi a veya b ye bölerek veya dönüşümü yapılarak denklemi çözülebilir. Aşağıda bi örnek çözerek bunu pekiştirelim.
denkleminin çözüm kümesini bulalım.
Öncelikle koşulunu sağlayıp sağlamadığını kontrol edelim.
a=1 , b= , c=1
koşulu sağlandığı için çözebiliriz.
Burada a=1 olduğu için herhangi bir paranteze almadan direkt eşitliğinden \sqrt3 \;\text{ yerine }\tan60^\circ yazalım ve çözelim.
Buradan sonrasını artık cosx=a denklemi gibi çözebiliriz.
1. Eşitlik
2. Eşitlik
İki eşitliğin çözüm kümelerini birleştirelim.
a.sinf(x)+b.cosf(x)=0 Biçimindeki Denklemlerin Çözüm Kümesi
Bu tür denklemlere (a ve b sayıları sıfırdan farklı olmak şartıyla) birinci dereceden homojen denklemler denir.
Bu denklemlerin çözümünde yukarıda yaptığımız gibi denklemin tamamını sinüs veya kosinüse bölerek direkt tanjant veya kotanjantlı bir ifadenin sonucuna ulaşabiliriz. Buradan da çözüm kümesini elde edebiliriz. Basit bir örnekle devam edelim.
denkleminin çözüm kümesini bulalım.
Çözüm kümesini yazmak istersek
a.cos2x+b.cosx.sinx+c.sin2x=0 Biçimindeki Denklemlerin Çözüm Kümesi
Bu tür denklemlere (a, b, c sayıları sıfırdan farklı olmak şartıyla) ikinci dereceden homojen denklem denir. Bu denklemlerin çözümünde ilk olarak her tarafı cos2x ile bölerek sadeleştiririz.
Elde ettiğimiz bu denklem aslında ikinci dereceden bir bilinmeyenli denklemdir. Burada tanjant yerine bir bilinmeyen tanımlayarak denklemi çözeriz ve sonuçları tanjanta eşitleyerek çözüm kümesine ulaşırız. Daha iyi anlamak için bir örnek çözelim.
denklemini çözelim.
Denklemin tamamını cos2x e bölersek
Bu noktada tanx yerine a bilinmeyenini yazarak denklemi çözelim. Bulacağımız değerleri tekrar tanjanta eşitleyerek çözüm kümesini bulalım.