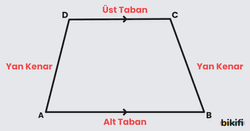
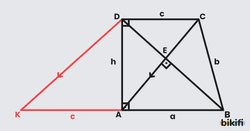
Yalnız iki kenarı paralel olan dörtgene yamuk denir. Üstteki şekilde AB ve DC kenarları paraleldir. Yan kenarların birbirine göre veya tabanlara göre duruşu yamuğun türünü belirler. Yamukların temel özelliklerinden sonra yamuk türlerine ve özelliklerine değineceğiz.
Yamuğun Özellikleri
Özellik 1
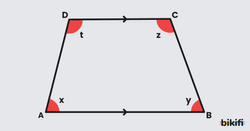
Yamuğun bir yan kenarının alt ve üst tabanla arasında kalan açıların toplamı 180° ‘dir.
Bu özelliğin temeli Z kuralına bağlıdır. Alt ve üst taban paralel olduğu için örneğin DC kenarının sol tarafından uzatırsanız bir Z şekli çıkacak ve t açısının yanındaki açı x’e eşit olacaktır. Böylelikle x ve t bir doğru açıyı oluşturdukları için toplamları 180° olacaktır.
Özellik 2
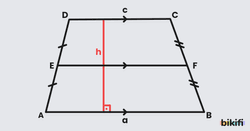
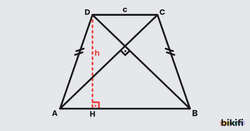
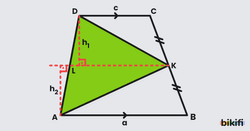
Bir yamukta yan kenarların orta noktaları birleştirildiğinde elde ettiğimiz doğru parçası yamuğun orta tabanıdır. Orta taban, alt ve üst tabana paralel ve ikisinin toplamının yarısı uzunluğundadır(kısaca ikisinin ortalaması).
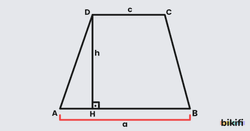
Bir yamukta alt ve üst taban arasındaki dik uzaklık yüksekliktir.
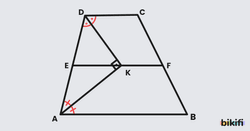
Yukarıdaki şekilde EF doğru parçası ABCD yamuğunun orta tabanı, h uzunluğu ise yüksekliktir.
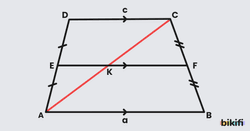
Bu formül üçgende benzerlikten gelmektedir. Yamuğun bir köşegenini çizdiğimiz zaman üçgenlere ayrılır. örneğin AEK ve ADC üçgenleri arasında kenar uzunluklarında 1’e 2 oranında bir benzerlik olduğu için EK kenarı DC kenarının yarısı olacaktır. Aynı mantığı sağ taraftaki üçgenler için de uygularsak aşağıdaki sonuçlara ulaşırız.
Özellik 3
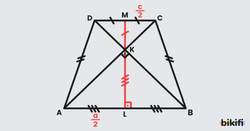
Bir yamukta yan kenarın tabanlarla arasında oluşan iç açıların açıortayları orta taban üzerinde dik kesişir.
Aşağıdaki şekli incelediğimizde A ve D köşelerinde bulunan açıların toplamının 180° olduğunu öğrenmiştik. ADK üçgenine baktığımızda bu iki açının da yarısı olduğuna göre bu açıların toplamı 90° olacaktır ve geriye kalan son açı da 90° olacağından bu bir dik üçgen olacaktır.
Bir dik üçgende dik köşeden hipotenüse indirilen kenarortay hipotenüs uzunluğunun yarısı olur. Bu özellik muhteşem üçlü adıyla da anılır ve yukarıdaki ADK üçgeninde bir muhteşem üçlü gözlenmektedir. EK doğru parçası dik köşeden uzanıp AD kenarını ortadan ikiye ayırdığı için aşağıdaki eşitlikler oluşur.
Muhteşem üçlü ismi eşitliklerden de anlaşıldığı üzere bu 3 uzunluğun birbirine olan eşitliklerinden gelir. Bu özellik çok önemlidir ve dik üçgen içeren çoğu soruda hatırlanmalıdır.
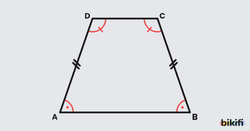
İkizkenar Yamuk
Yan kenarlarının tabanlarla yaptığı açıları eşit olan ve bu nedenle yan kenarları birbirine eşit olan yamuğa ikizkenar yamuk denir.
Özellik 1
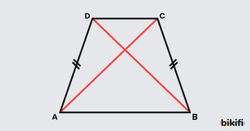
İkizkenar yamuk simetrik bir yapıya sahip olduğu için köşegenleri birbirine eşittir.
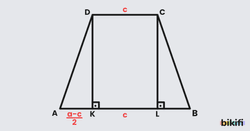
Bir ikizkenar yamukta üst tabanın kenarlarından alt tabana dikmeler indirdiğimizde, üst tabanın altında kalan kısım üst tabana geri kalan kısım ise alt tabandan üst tabanı çıkardığımızda kalan sonucun yarısı sağ tarafa diğer yarısı sol tarafta kalan parçaya eşit olacaktır.
Özellik 2
Köşegenleri dik kesişen bir ikizkenar yamuğun yüksekliği alt ve üst tabanın toplamının yarısına eşittir.
İspat
Dik üçgenlerdeki muhteşem üçlü özelliği yine karşımıza çıkıyor. Köşegenlerin kesiştiği nokta(K) yamuğu x ekseninde tam ortaladığı için kesiştikleri noktadan tabanlara dikmeler indirdiğimizde tabanları iki eşit parçaya bölecek ve indirdiğimiz dikmeler tabanların yarısına eşit olacaktır.
Dik Yamuk
Yan kenarlarından sadece bir tanesi tabanlara dik olan yamuğa dik yamuk denir.
Özellik 1
Köşegenleri dik kesişen dik yamukta yükseklik alt ve üst tabanın çarpımlarının kareköküne eşittir.
İspat
Dik yamuğun alt tabanı olan AB kenarı uzatıp, D köşesinden AC köşegenine paralel bir doğru çizerek alt tabanla birleştirelim. ADB üçgeninin D köşesi 90° olacaktır ve buradan indirilen bir dikme yine bir üçgen kuralı olan öklid bağıntılarını aklımıza getirecektir.
Öklid bağıntılarına göre dik köşeden hipotenüse dikme indirdiğimiz zaman hipotenüsün ayrılan parçalarının çarpımı indirilen dikmenin karesine eşit olur.
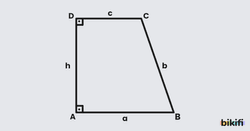
Yamuğun Alanı
Özellik 1
Taban uzunluklarının toplamının yükseklikle çarpımının yarısı bize yamuğun alanını verir.
İspat
Yamuğun bir köşegenini çizdiğimizde karşımıza iki tane üçgen çıkacaktır. Bu üçgenlerin ikisinin de alanını bulup toplarsak yamuğun alanına ulaşırız.
Özellik 2
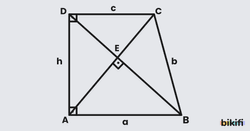
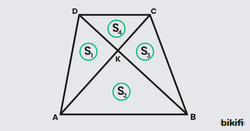
Bir yamukta köşegenleri çizdiğimiz zaman içeride 4 tane üçgen oluşur ve bu üçgenlerin alanları arasında bağıntılar vardır. Bu bağıntılar her yamuk için geçerlidir.
İspat 1
DAB ve CAB üçgenlerini ele aldığımızda alanlarını hesaplarken taban uzunlukları ve yükseklikleri eşit olduğundan alanları da eşit olacaktır. DAB üçgeninin alanı S + S, CAB üçgeninin alanı S + S olduğuna göre S ikisinde de ortak olduğu için onu çıkartırsak S ve S birbirine eşit olacaktır.
İspat 2
Yüksekliği eşit olan üçgenlerde taban uzunlukları arasındaki oran alanları arasındaki oranı verir. DAK ve DCK üçgenlerini incelediğimizde AC köşegenini taban kabul ettiğimizde iki üçgenin de yükseklikleri D köşesinden AC köşegenine ineceğinden eşit olacak. O zaman taban uzunları olan AK ve KC uzunlukları arasındaki oran bize üçgenlerin alanları arasındaki oranı verecektir.
Aynı orantıyı BAK ve BCK üçgenleri arasında kurarsak
eşitliğini elde edeceğiz. Artık alanlar arasında direkt orantı kurabiliriz.
Özellik 3
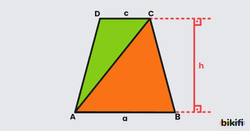
Yamuğun bir yan kenarının tabanlarla kesiştiği noktadan diğer yan kenarın orta noktasına doğular çizdiğimizde oluşan büyük üçgenin alanı yamuğun alanının yarısı olur.
İspat
Yamuğun orta tabanını çizdiğimizde bahsettiğimiz boyalı üçgenin alanı ikiye ayrılır. İki üçgenin de alanını bulup topladığımızda bize yamuğun alanının yarısını verecektir.