Elektrot Potansiyelleri

Standart Yarı Hücre İndirgenme Potansiyelleri

Bir yarı hücredeki elektrodun potansiyeli deneyle veya teorik olarak ölçülemez. Çünkü yarı hücre tepkimeleri tek başına gerçekleşmez. Yükseltgenmenin gerçekleşmesi için indirgenmeye, indirgenmenin gerçekleşmesi için de yükseltgenmeye ihtiyaç vardır. Bu çıkmazdan kurtulmak için bir referans elektrot seçmek ve bu elektrot potansiyelini kabul görmüş bir değerle ifade etmek yoluna gidilmiştir. Bir elektrodun potansiyeli, referans elektrot ile hazırlanan elektrokimyasal hücrenin potansiyelinin ölçülmesiyle hesaplanabilir.

Standart Hidrojen Elektrodu

Uluslararası Temel ve Uygulamalı Kimya Birliği (IUPAC) tarafından referans elektrodu olarak hidrojen elektrodu seçilmiştir ve bu elektrodun standart elektrot potansiyeli sıfır (0) volt olarak kabul edilmiştir. Standart hidrojen elekrodu, 25 °C’de 1M H+ iyonu içeren asit çözeltisindeki platin elektrot üzerine 1 atm basıncında H gazı gönderilmesi ile oluşturulur.

Standart şartlarda (25 °C, 1atm ve 1 M çözelti) bir elektrotta oluşan indirgenme eğiliminin ölçüsüne standart elektrot potansiyeli denir ve bu potansiyel ile gösterilir. Standart elektrot potansiyelleri her zaman indirgenme şeklinde yazılır. Bu nedenle standart indirgenme potansiyeli şeklinde de isimlendirilir. Aynı zamanda her elektrodun standart potansiyeli o elektrodun elektron çekme gücünün ölçüsüdür.

Standart hidrojen elektrodu diğer tüm elektrodların standart elektrot potansiyellerini bulmak için kullanılır. Herhangi bir elektrot, standart hidrojen elektrodu ile birleştirilerek bir elektrokimyasal hücre yapılır ve bu hücrenin standart potansiyeli ölçülür. Hidrojen elektrodunun standart indirgenme potansiyeli diğer elektrodun standart indirgenme potansiyeline eşit olur.

Örnek

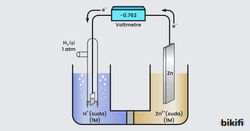
Zn elektrodun standart indirgenme potansiyelini belirlemek için bir düzenek kurulmuştur ve voltmetre değeri 0,763 V olarak ölçülmüştür.

Hazırlanan galvanik hücrede Zn elektrodun yüzeyinde aşınma olduğu gözlenir. Bu aşınma, Zn metalinin iyonlarına yükseltgenmesinden kaynaklanır. Yükseltgenmenin olduğu elektrot anot, indirgenmenin olduğu elektrot katottur.

Yarı hücrelerdeki tepkimeler ve hücrenin denklemi şu şekildedir:

Hidrojen elektrodun standart indirgenme potansiyeli 0 olduğundan ve Zn yarı hücresinde yükseltgenme gerçekleştiğinde voltmetrede okunan değer, Zn elektrodun yükseltgenme potansiyeli olur. Zn elektrodun standart indirgenme potansiyelini hesaplamak için Zn elektroda ait tepkimenin ters çevrilmesi gerekir. Bu durumda yükseltgenme potansiyelinin işareti değişir.

Zn elektrodun standart indirgenme potansiyeli -0,763 V olarak bulunur. Bu örnekte hidrojen elektrodu yardımıyla Zn elektrodun standart potansiyeli hesaplanmıştır. Benzer şekilde diğer maddeler için standart elektrot potansiyeli hesaplanabilir.

Hücre Şeması Gösterimi

Elektrokimyasal hücrelerin gösterim kolaylığı için şema olarak gösterimi kullanılır. Bu gösterime hücre şeması denir.

Hücre şeması şu kurallara göre yazılır:

Anot ve anodun içinde bulunduğu çözelti ile ilgili bilgiler sol tarafa, katot ve katodun içinde bulunduğu çözelti ile ilgili bilgiler sağ tarafa yazılır.
Farklı fazlar arasındaki sınır tek dikey çizgi | ile ayrılır.
İki ayrı hücre arasındaki tuz köprüsü çift dikey çizgi || ile gösterilir.

Üsteki hücrenin şematik gösterimi şu şekildedir:

Bazı Elementlerin Standart İndirgenme Potansiyelleri

Yarı Tepkime	Standart İndirgenme Potansiyeli [V]
F₂+2e^– → 2F^–	+2,870
Au⁺³+3e^– → Au(k)	+1,498
Cu⁺+e^– → Cu(k)	+0,521
Cu⁺²+2e^– → Cu(k)	+0,337
2H⁺+2e^– → H₂(g)	0,000
Cr⁺³+e^– → Cr⁺2	-0,408
Al⁺³+3e^– → Al(k)	-1,662
Na⁺+e^– → Na(k)	-2,714
K⁺+e^– → K(k)	-2,931
Li⁺+e^– → Li(k)	-3,040
Yarı Tepkime	Standart İndirgenme Potansiyeli [V]

Yukarıdaki tabloda verilen indirgenme potansiyellerine bakılarak elektrotlar hakkında bilgi edinilebilir. Negatif işaretli olanlar kendiliğinden yükseltgenebilen, pozitif işaretli olanlar ise kendiliğinden indirgenebilen maddelerdir. Tabloya bakıldığında yükseltgenme eğilimi en büyük olanın Li+ iyonu, indirgenme eğilimi en büyük olan türün ise F elementi olduğu görülür.

Standart Elektrot İndirgenme Potansiyeli Hesaplanması

📌 Standart elektrot indirgenme potansiyeli hesaplanırken şu eşitlik kullanılabilir:

📝Standart hücre hesaplarında aşağıdaki ilkelerden yararlanılır:

Bir galvanik hücrede elektrotların hangisinin anot ya da katot olarak görev yapacağı standart elektrotların potansiyellerine bağlıdır. İndirgenme potansiyeli büyük olan elektrot, katot olarak görev yapar ve indirgenme tepkimesi gerçekleşir. İndirgenme potansiyeli küçük olan elektrot ise anot olarak görev yapar ve yükseltgenme tepkimesi gerçekleşir.

Yukarıdaki tepkimelerde bakır elementinin (Cu) standart indirgenme potansiyeli büyük olduğu için Cu elektrot katot, Zn elektrot ise anot olarak görev yapar.
Bir yarı hücre ters çevrildiğinde değerinin işareti değişir.

Elektrot potansiyeli, birim yüke(bir elektrona) verilen enerjidir. Elektron sayısının artması ya da azalması bu değeri değişmez. Bu nedenle bir yarı hücredeki katsayının değiştirilmesi değerini etkilemez.

Örnek

Aşağıdaki yarı hücrelerden bir galvanik hücre oluşturuluyor. Oluşan galvanik hücrenin potansiyelini hesaplayalım.

Çözüm: değeri küçük olan Li yarı hücresinde yükseltgenme, değeri büyük olan Pb yarı hücresinde ise indirgenme olur.

Anot tepkimesi
Katot tepkimesi
Elektron sayılarını eşitlemek için anot tepkimesi ikiyle çarpılır fakat etkilenmez.
Anot tepkimesi
Katot tepkimesi
Net tepkime:

Metallerde Aktiflik

Metallerin aktifliği elektron verme potansiyelleriyle doğru orantılıdır. Standart indirgenme elektrot gerilimi en küçük olan elementin yükseltgenme eğilimi ve aktifliği en büyüktür. “Bazı Elementlerin Standart İndirgenme Potansiyelleri” adlı tabloda görüldüğü gibi standart indirgenme elektrot gerilimi en küçük olan lityumun en aktif element olduğu görülür.

✍ Standart indirgenme potansiyeli negatif olan metallere aktif metal, pozitif olanlara ise pasif metal denir.

Standart Elektrot potansiyeli yöntemi sayesinde metallerle ilgili aşağıdaki bilgilere sahip olunabilir.

Metallerin aktifliği
Metallerde aşınma olup olmayacağı (metal atomu, çözeltideki metal iyonundan aktif ise metal aşınır).
Metallerin asitlerle tepkime verme durumu
Asitlerle tepkime veren metallerin H₂(g) oluşturup oluşturmayacağı
Metal tepkimesinin istemli olup olmadığı

Standart Elektrot Potansiyeli ve İstemlilik

Standart elektrot potansiyelleriyle hesaplanan pil potansiyelleri sayesinde tepkimenin istemliliğine karar verilebilir. değeri 0’dan büyükse tepkime istemli, 0’dan küçükse tepkime istemsiz olur. değerinin hesaplanması için anot ve katot standart elektrot potansiyelleri toplanır.

📝Örnek

redoks tepkimesinin istemli olarak gerçekleşip gerçekleşmeyeceği standart elektrot potansiyellerine bakılarak belirlenebilir.

değerlerine göre iyonunun standart indirgenme elektrot potansiyeli iyonundan daha büyüktür. Bu nedenle indirgenir, yükseltgenir.
Anot tepkimesi:
Katot tepkimesi:
Net tepkime:
değeri 0’dan büyük olduğu için tepkime istemlidir.

Standart Elektrot Potansiyelini Etkileyen Faktörler

Elektrokimyasal hücre potansiyelinin doğru şekilde ölçümü önemlidir. Şimdiye kadar hücre potansiyellerinin hesabında standart durum (25 C’de 1,0 M, gazlar için ise 1,0 atm) kullanılmıştır. Fakat deneysel ölçümler her zaman standart şartlarda yapılmaz.

📌 Hücre potansiyelini etkileyen faktörler şunlardır:

Kullanılan cinsi
- Hücre potansiyeli iki elektrodun standart potansiyeli arasındaki fark olduğu için yarı hücrelerde anot ve katot olarak kullanılan elektrotlar değişik türden kullanıldığında hücre potansiyeli değişir. Yani kısaca, elektrot cinsi değişir ise potansiyel fark da değişir.
Sıcaklık
- Pil tepkimeleri gerçekleşirken enerji açığa çıkar. Bu demektir ki pil tepkimeleri ekzotermiktir.
- Yukarıdaki pil tepkimenin sıcaklığı artırılırsa denge girenler yönüne kayar ve pil gerilimi azalır. Eğer sıcaklık azaltılırsa denge, ürünler yönüne kayar ve pil potansiyeli artar.
Çözelti Derişimleri
- Pil potansiyelini etkileyen diğer bir etken çözeltinin derişimidir. Yarı hücrelerdeki çözeltilerin derişimlerinin değişimi elektrokimyasal hücre potansiyelini etkiler.
- Bir pil tepkimesinde katot yarı hücresinde derişim arttırıldığında ya da anot yarı hücresindeki derişim azaltıldığında tepkime, ürünler yönünde ilerler ve hücre potansiyeli artar.
- Diğer taraftan katot yarı hücresindeki derişim azaltılırsa ya da anot yarı hücresindeki derişim artırılırsa tepkime, girenler yönünde ilerler ve hücre potansiyeli azalır.
- Hücre potansiyeli ile derişim arasındaki ilişkiyi ilk kez Alman kimyacı Walther Nernst (Valther Nerst) ortaya koymuştur.
Basınç (gaz ‘lar için)
- Basınç değişimi sadece SHE içeren galvanik pillerde etkilidir.

Nernst Eşitliği (Derişim Etkisi)

Standart olmayan şartlardaki hücre potansiyelidir.
Aynı hücrenin standart şartlardaki hücre potansiyelidir.
n: Tepkimede alınan veya verilen elektron sayısıdır.
Q: Tepkime oranıdır (Denge sabiti).

tepkimesinde bir pilin potansiyeli genel olarak

eşitliğiyle hesaplanır. Bu eşitlikte ve deney şartlarındaki ve iyonlarının derişimleridir.

Derişim Pilleri

Elektrolit derişimleri farklı olan ve aynı metalden yapılmış iki elektrodun biri anot, diğeri katot olacak şekilde kullanılmasıyla pillere derişim pilleri denir.

Derişim Pillerinin Özellikleri

Elektrolit derişimleri aynı olursa Nernst eşitliğine göre logQ=0 olacağından pil potansiyeli =0 olur ve bu şekildeki bir pil çalışmaz.
Eğer elektrolit derişimleri farklı olursa sadece bu farktan yararlanan bir pil yapılabilir. Bu pil, derişimler birbirine eşitleninceye kadar çalışır.
Bu pilin çalışması için değerinin pozitif olması gerekir. değerinin pozitif olması için Nernst eşitliğine göre logQ değerinin negatif çıkması gerekir. Bu nedenle derişim pillerinde derişimi az olan yarı hücre daima anot olarak alınır.

📝 Örnek