Kütle skaler bir büyüklük olup madde miktarıyla ilgili bir özelliktir. Ağırlık ise, yerin uyguladığı çekim kuvvetidir. Ağırlık vektörel bir büyüklüktür ve birimi, kuvvetin birimi ile aynıdır.
Bir cismin ağırlık kuvveti düşey doğrultuda olup yerin merkezine yöneliktir. Bir cismin kütlesi Dünya ve uzayın hiçbir yerinde değişmez. Ağırlığı ise çekim ivmesinin değişken olmasından dolayı değişebilir.
Kütle Merkezi
Yer çekimli ortamda cisimlere etki eden kuvvetlerden biri de kendi ağırlığıdır. Katı cisimler küçük parçalardan meydana gelir ve her parçacığa etki eden ”m*g” kuvveti vardır. Bu kuvvetler aynı yönlü paralel kuvvetlerdir. Bu kuvvetlerin bileşkesinin yeri ağırlık merkezi adınıalır. Kısaca cismi dengede tutan noktaya denir.
- Cisme başka kuvvet etki etmediği ve g değişmediği sürece ağırlık merkezinin olduğu nokta aynı zamanda kütle merkezidir.
- Yer çekimi olmadığında ağırlık merkezinden söz edilemez.
- Kısacası cismin kütle merkezi ile ağırlık merkezinin yeri aynıdır ve momentler hesaplanırken cismin bütün ağırlığının ağırlık merkezinde toplandığı kabul edilir.
Kütle Merkezinin Özellikleri
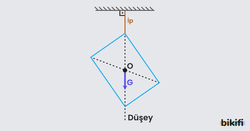
- Bir cisim herhangi bir yerinden iple asılır ise ipin uzantısı cismin kütle merkezinden geçecek şekilde cisim dengede kalır.
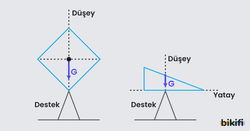
- Bir cisim destek üzerinde dengede kalabilmesi için düşey destek tepki kuvveti doğrultusunun, kütle merkezinden geçmesi gerekir. Şekilde görülen cisimler destek üzerinde dengededir çünkü kütle merkezi desteğin olduğu yerdeki düşey doğrultu üzerindedir.
- Bir cismin yerde devrilmeden durabilmesi için cismin kütle merkezinin düşey doğrultusunun cismin yere temas eden yüzey alanının içinden geçmesi gerekir.
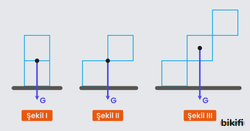
Yukarıdaki cisimlerden;
- Şekil-I deki cisim dengede kalır çünkü kuvvetin doğrultusu temas yüzeyi içerisindedir.
- Şekil-II tam sınırda olduğu için dengede kalabilir.
- Şekil-III deki cisim dengede kalamaz çünkü kuvvet doğrultusu temas yüzeyi dışından geçer.
Koordinat Ekseni Üzerindeki Cisimlerin Kütle Merkezi
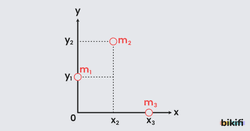
Birden çok cisimden meydana gelen düzenekte bütün kütlelerin toplandığı varsayılar noktaya tüm cisimlerin ortak kütle merkezi denir.
Bir yüzey üzerinde bulunan kütlelerinden oluşan cisimlerin koordinatları;
ise, sistemin ortak kütle merkezi x ve y koordinatları ile belirtilir.
Kütle merkezinin x ekseni üzerindeki yeri;
Kütle merkezinin y ekseni üzerindeki yeri;
dir.
Sistemin kütle merkezi ise; şeklinde belirtilen noktadır.
Düzgün Geometrik Yapılı Cisimlerin Kütle Merkezi
Geometrik merkezi olan homojen cisimlerin kütle merkezi ile geometrik merkezi aynı noktadır.
- Düzgün ve türdeş çubuğun kütle merkezi, çubuğun tam orta noktasındadır.
- Düzgün ve türdeş olan kare, dikdörtgen ve paralelkenar şeklindeki iki boyutlu cisimlerin kütle merkezi köşegenlerin kesişme noktasıdır.
- Düzgün ve türdeş çember, daire ve kürenin kütle merkezi, cisimlerin geometrik merkezleridir.
- Türdeç silindir, dikdörtgen prizma ve küpün merkezi, ürt ve alt taban merkezlerini birleştiren doğrunun tam ortasındadır.
Bir Sistemde Kütle ve Ağırlık Merkezinin Bulunması
- Sistem basit geometrik parçalara ayrılır.
- Her bir parçanın kütle merkezi bulunup ağırlığı aşağıya doğru gösterilir.
- Sisteme eklenen parça varsa eklenen parçanın ağırlığı aşağı yönde, çıkarılan parça varsa ağırlığı yukarı yönde gösterilir.
- Paralel kuvvetlerin bileşkesinin yeri hesaplanır.Bileşkenin uygulama noktası sistemin kütle merkezinin yerini verir.