Vektörlerin Özellikleri
Bir doğru üzerinde belli bir noktadan başlayıp başka bir noktada biten yönlü doğru parçasına vektör denir. Bu doğru parçalarının vektör olduğunu belirtmek için üzerine işareti koyulur. Vektörlerin 4 temel özelliği vardır:
- Başlangıç noktası
- Doğrultusu
- Yönü
- Büyüklüğü

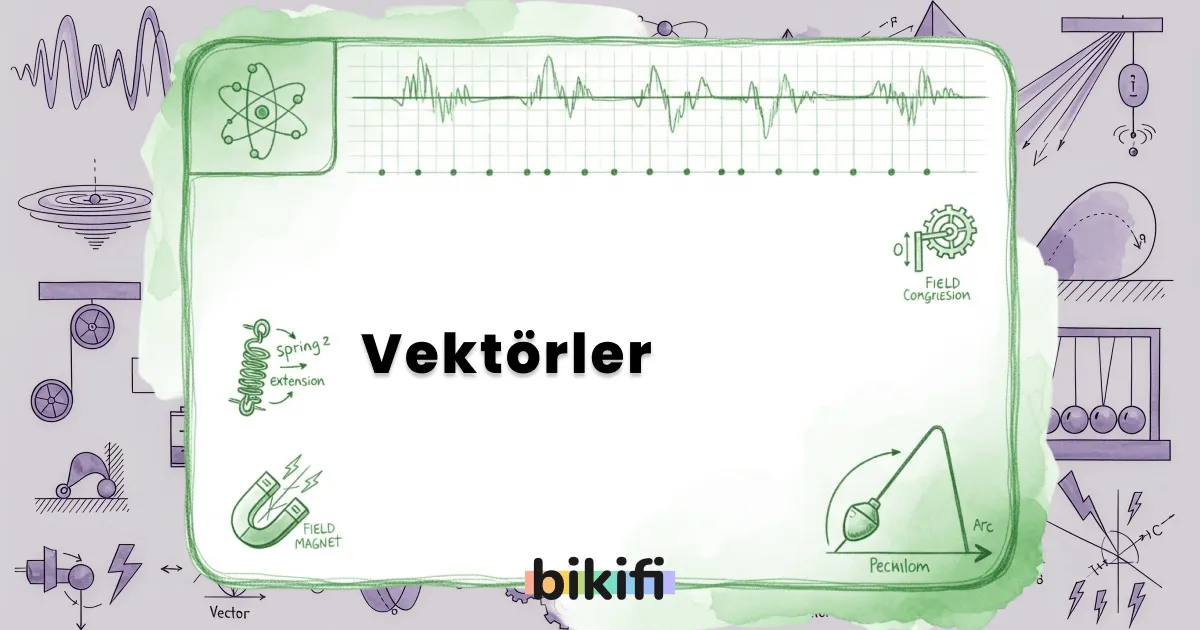
Şekilde görüldüğü gibi başlangıç noktası X bitiş noktası Y olan bir K vektörü gösterilmektedir. Vektörün sonundaki ok vektörün yönünü gösterir. Vektörün üzerinde bulunduğu doğru, vektörün doğrultusu olarak ifade edilir. Bu doğru parçasının uzunluğu ise vektörün büyüklüğüdür. Vektörün büyüklüğü mutlak değer içinde yazılarak veya üzerinde işareti olmadan normal bir yazımla K olarak ifade edilebilir.
Doğrultusu, yönü ve büyüklüğü aynı olan vektörlere eşit vektörler denir ve birbirine eşit A ve B vektörü için yazılabilir. Eşit vektörlerin başlangıç noktaları farklı olabilir, bu da bize bir vektörün özelliklerinin değiştirilmeden bir noktadan başka bir noktaya taşınması imkânını verir (konunun ilerleyen kısımlarında çok işimize yarayacaktır). Doğrultusu ve büyüklüğü aynı fakat yönü farklı vektörlere zıt vektörler denir ve birbirine zıt C ve D vektörleri için yazılabilir.

Bir vektör, 1’den farklı pozitif bir sayı ile çarpılırsa sadece büyüklüğü bu sayı kadar büyür veya küçülür. Eğer 1’den farklı negatif bir sayı ile çarpılırsa hem büyüklüğü hem de yönü değişecektir. Her iki durumda da doğrultu değişmez.
Vektörlerin Dik Koordinat Sisteminde İki ve Üç Boyutlu Olarak Çizilmesi
Vektörler koordinat düzlemine büyüklükleriyle orantılı olarak çizilirler. Örneğin bir birim uzunluğunda çizilen vektör 10N büyüklüğünde ise 3 birim uzunluğunda çizilen vektör 30N büyüklüğünde olur. Vektörü koordinat düzleminde gösterirken hiçbir özelliğini değiştirmeden başlangıç noktasını koordinat düzleminin orijin(0,0) noktasına taşıyarak buradan başlatırız.
Vektörü iki boyutta göstermek için x-y koordinat düzlemi kullanılır. Bir A vektörünü iki boyutta şeklinde gösteririz. Burada , A vektörünün x eksenindeki değerini; , A vektörünün y eksenindeki değerini gösterir.
Vektörü üç boyutta göstermek için ise x-y-z koordinat sistemi kullanılır. Bir B vektörünü üç boyutta şeklinde gösteririz. Burada , B vektörünün x eksenindeki değerini; , B vektörünün y eksenindeki değerini ve , B vektörünün z eksenindeki değerini gösterir.
Bileşke Vektör
Bileşke Vektörün Tanımı
İki veya daha fazla vektörel büyüklüğün toplanması ile elde edilen yeni vektöre bileşke vektör denir. ile gösterilir. Bileşke vektör aynı zamanda toplanan vektörlerin yaptığı etkiyi, tek başına yapabilen vektördür.
Bileşke Vektörün Ve Büyüklüğünün Bulunması
Bileşke vektörünü farklı yöntemlerle bulabiliriz.
Uç uca ekleme yöntemi
Bu yöntem iki veya daha fazla vektörün tek işlem yapılarak bulunmasını sağlar. Bu yöntemi kullanırken uygulanacak basamaklar sırasıyla şöyledir:
- Verilen vektörlerden herhangi biri çizilir.
- Verilen vektörlerden herhangi biri çizilir.
- İkinci vektörün başlangıç noktası, ilk çizilen vektörün bitiş noktasına gelecek şekilde ikinci vektör çizilir.
- Bu işleme tüm vektörler bitene kadar devam edilir.
- İlk vektörün başlangıç noktasından, son vektörün bitiş noktasına bir vektör çizilir ve bu bileşke vektör olur.
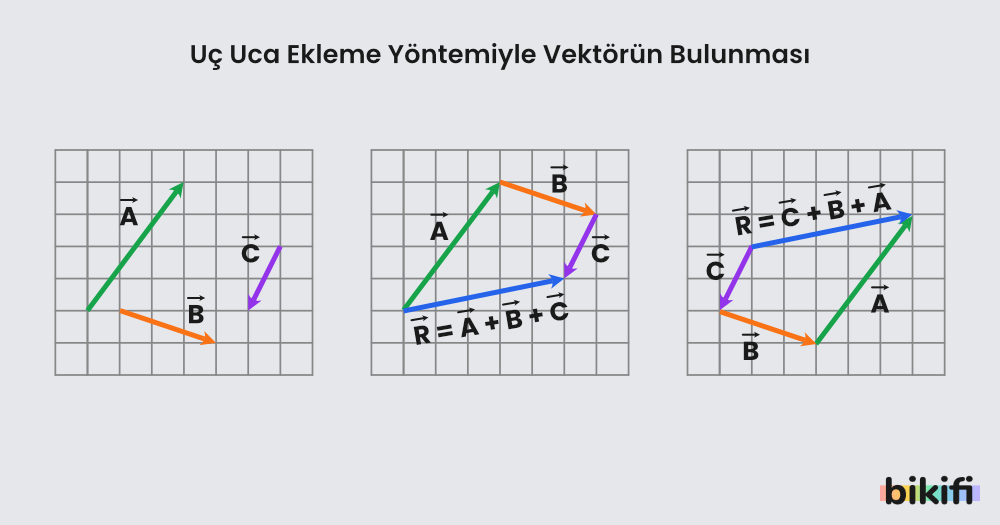
Yön ve doğrultuları verilen , , vektörlerinin bileşkesi vektörünün uç uca ekleme yöntemiyle bulunması yukarıdaki şekilde gösterilmiştir. Vektörlerin toplanmasında değişme özelliği vardır, bu yüzden toplamı hangi sırayla yaptığımızın önemi yoktur.
Paralelkenar yöntemi
Bu yöntem daha çok iki vektörün bileşkesini bulmakta kullanılır. Daha fazla vektör için de kullanılabilir fakat işlem çokluğundan çok tercih edilmez. Bu yöntemi kullanırken uygulanacak basamaklar sırasıyla şöyledir:
- İki vektör aynı noktadan başlayacak şekilde çizilir.
- Her bir vektörün bitiş noktasından diğer vektöre paralel çizilir.
- Vektörlerin başlangıç noktasından, çizilen paralellerin kesişim noktasına doğru çizilen vektör, bileşke vektör olur.
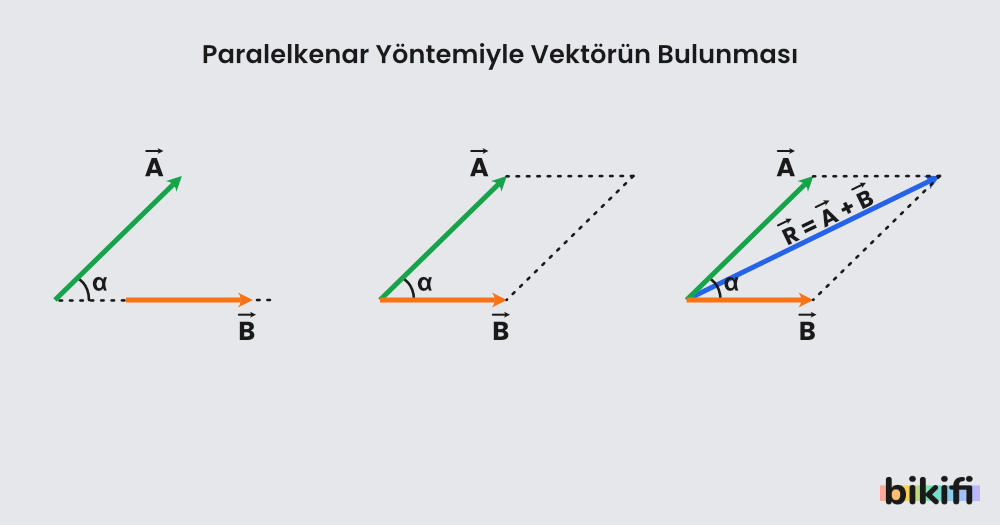
Aralarında kadar açı olan ve vektörlerinin bileşkesi vektörünün paralelkenar yöntemiyle bulunması yukarıdaki şekilde gösterilmiştir. Paralelkenar yönteminde bileşke vektörünün büyüklüğü kosinüs teoremiyle hesaplanır.
Bileşenlerine Ayırma Yöntemi
Bu yöntemle çok sayıda vektörün bileşkesi kolaylıkla bulunabilir. Bu yöntemde, vektörlerin dik koordinat sistemindeki gibi (x,y) koordinat noktalarına ihtiyaç vardır. Bu yöntemi kullanırken uygulanacak basamaklar sırasıyla şöyledir:
- Her bir vektörün başlangıç noktası orijin(0,0) olarak kabul edilir ve her vektörün (x,y) koordinat noktaları tespit edilir. (Bulunan bu x ve y değerleri aslında vektörün o eksenlerdeki bileşenin büyüklüğüdür.)
- Bileşke vektörün x ekseni üzerindeki bileşeninin büyüklüğünü bulmak için tüm vektörlerin x bileşenlerinin büyüklükleri toplanır.
- Bileşke vektörün y ekseni üzerindeki bileşeninin büyüklüğünü bulmak için benzer biçimde, tüm vektörlerin y bileşenlerinin büyüklükleri toplanır.

x ve y bileşenleri verilen , , vektörlerinin bileşkesi vektörünün bileşenlerinin bulunması yukarıdaki şekilde gösterilmiştir. Bileşkenin büyüklüğünü ise bileşenlerinin karelerini bileşkenin keresine eşitleyerek (Pisagor Teoremi) bulabiliriz.
Vektörlerde Çıkarma İşlemi, Fark Vektör
Vektörlerde çıkarma işleminde “bir vektörün negatifi” tanımından yararlanılır. Bunun anlamı bize verilen ve vektörlerinin farkı istendiğinde bu ifadeyi şeklinde yazabilmemizdir. Bundan sonra bileşke vektörü bulma bölümünde gösterdiğimiz yöntemleri uygulayabiliriz.
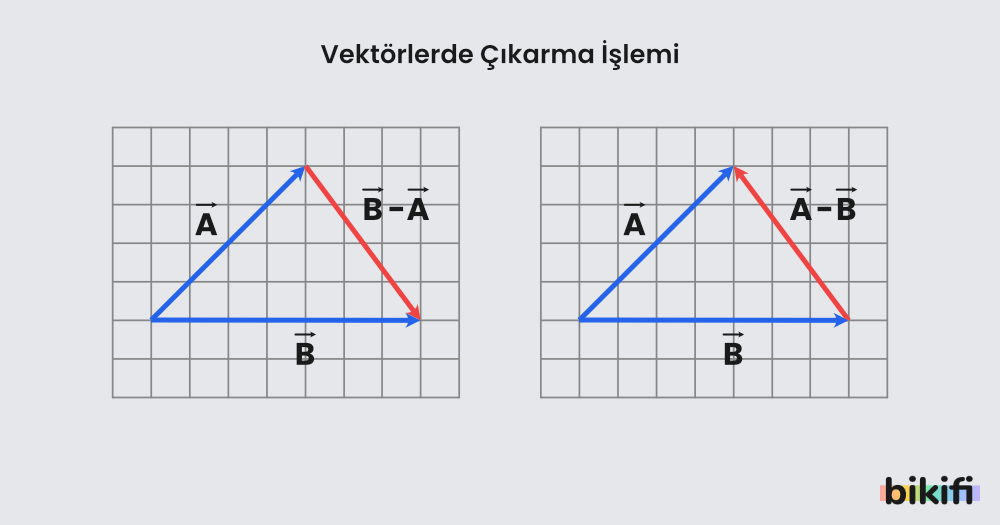
Fark vektörünü bulmak için pratik bir yol daha vardır. Farkı istenilen iki vektör paralelkenar yöntemindeki gibi başlangıç noktaları birleştirilir, sonra bu vektörlerin bitiş noktaları arasına bir vektör çizilir. Bu vektör fark vektörüdür ve yönü “+” olan vektöre doğrudur. Yukarıdaki şekilde de gösterildiği gibi farkı istenirse bitiş noktaları birleştirilir ve yönü “+” işaretli olan vektörüne doğru olur. Eğer farkı istenirse aynı işlemler yapılır ama en son yönü vektörüne doğru olur.
Vektörlerin Bileşenleri
Vektörlerin koordinat sisteminde eksenler üzerindeki izdüşümlerine vektörün bileşenleri denir. Aslında bu bölüme gelene kadar vektörlerin bileşenlerini bulmayı öğrendik. Bu bölümde açıdan da bileşen bulmayı öğreneceğiz. Vektörün x ekseniyle yaptığı açının sinüs ve kosinüs değerleri bu vektörün x ve y bileşenlerini verir.
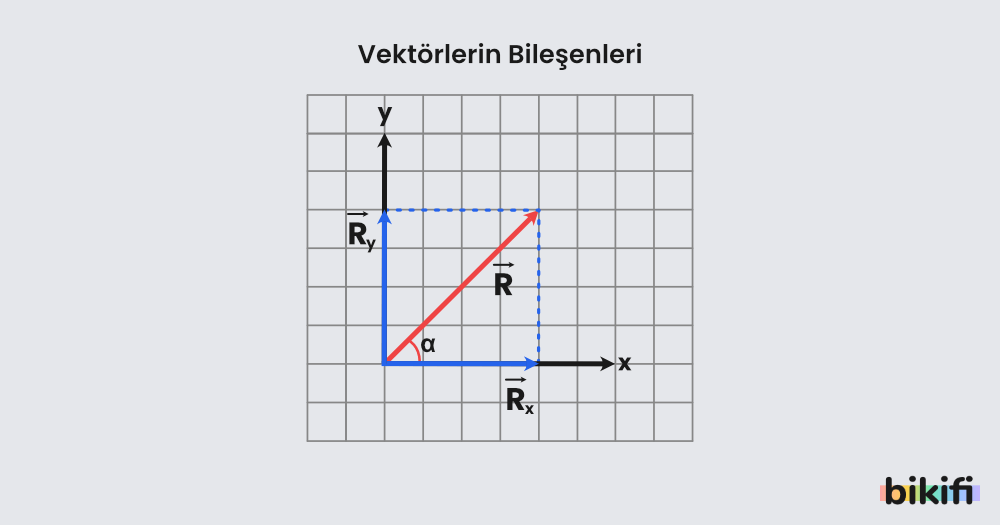
Şekildeki vektörünün x eksenindeki bileşenini bulmak için kosinüs, y eksenindeki bileşeni için ise sinüsü kullanabiliriz.