Üçgenler, geometrinin en temel şekillerinden biridir ve günlük hayatımızda sıkça karşılaştığımız yapıların temelini oluşturur. Köprülerin sağlamlığından, çatıların dayanıklılığına kadar pek çok alanda üçgenlerin özelliklerinden yararlanırız. Bu derste, üçgenlerin içinde çizebileceğimiz özel doğru parçalarını ve bunların birbirleriyle olan ilişkilerini öğreneceğiz. Bu yardımcı elemanlar sayesinde üçgenlerle ilgili problemleri daha kolay çözebilir, mühendislik ve mimarlık gibi alanlarda kullanılan temel prensipleri anlayabilirsiniz.
Üçgenin Açıortayları
Bir açıyı tam ortadan ikiye bölen doğruya açıortay denir. Üçgende her köşeden karşı kenara doğru açıortay çizebiliriz. Bu açıortaylar, üçgenin içinde ya da dışında olabilir.
Üçgenin İç Açıortayı ve Özellikleri
İç açıortay, bir köşedeki açıyı iki eşit parçaya bölen ve karşı kenarı kesen doğru parçasıdır. Bir kağıdı katlayarak açıortayı kolayca bulabilirsiniz. Açının bir kenarını diğer kenarının üzerine gelecek şekilde katlarsanız, kat izi açıortayı verir.
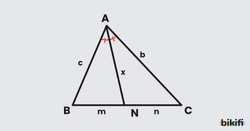
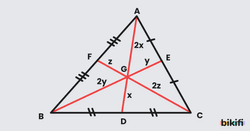
İç Açıortay Teoremi, üçgende çok önemli bir ilişkiyi ortaya koyar. Yukarıdaki ABC üçgenindeki gibi A köşesinden çizilen açıortay, BC kenarını N noktasında kesiyor. Bu durumda:
Bu formül bize açıortayın karşı kenarı, komşu kenarlara orantılı olarak böldüğünü gösterir. Örneğin, bir üçgenin kenarları 6 cm ve 9 cm ise, açıortay karşı kenarı 2:3 oranında böler.
Açıortay üzerindeki her nokta, açının kollarına eşit uzaklıktadır. Bunu futbol sahasında penaltı noktasının belirlenmesinde görebiliriz. Penaltı noktası, kale direklerine giden doğruların oluşturduğu açının ortasında, her iki direğe de eşit açıyla bakacak şekilde konumlandırılmıştır.
Üçgenin İç Açıortaylarının Kesim Noktası
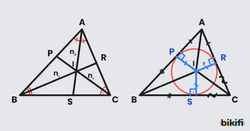
Üçgenin üç iç açıortayı tek bir noktada kesişir. Bu noktaya iç teğet çemberin merkezi denir ve genellikle I harfi ile gösterilir. Bu nokta çok özeldir çünkü üçgenin her üç kenarına da eşit uzaklıktadır.
İç teğet çember, üçgenin içinde çizilebilecek en büyük çemberdir ve üçgenin her üç kenarına da teğettir (değer). Bu çemberin yarıçapı, merkez noktasından kenarlara indirilen dikmelerin uzunluğuna eşittir.
Açıortayların kesim noktasında oluşan açılar da özel ilişkilere sahiptir. Örneğin, A açısının ölçüsü α ise, açıortayların kesim noktasında A köşesinin karşısında oluşan açı olur.
Üçgenin Dış Açıortayı ve Özellikleri
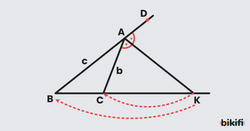
Bir üçgenin köşesindeki dış açı (bir kenarın uzantısı ile diğer kenar arasında oluşan açı), dış açıortay ile ikiye bölünür. Dış açıortay da tıpkı iç açıortay gibi özel bir orana sahiptir:
Burada K noktası, dış açıortayın karşı kenarın uzantısını kestiği noktadır.
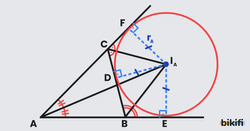
İlginç bir özellik olarak, iki dış açıortay ve bir iç açıortay bir noktada kesişir. Bu nokta dış teğet çemberin merkezidir. Bir üçgende üç tane dış teğet çember çizilebilir. Her biri üçgenin bir kenarına ve diğer iki kenarın uzantılarına teğettir. Kare kağıt katlama problemlerinde bu özellikten yararlanılır.
Üçgenin Kenarortayları
Kenarortay, üçgenin bir köşesinden karşı kenarın orta noktasına çizilen doğru parçasıdır. Her üçgende üç kenarortay vardır ve bunlar üçgeni altı küçük üçgene ayırır.
Kenarortay Tanımı ve Özellikleri
Kenarortayların en önemli özelliği, üçte kesişmeleridir. Bu kesişim noktasına ağırlık merkezi denir ve G harfi ile gösterilir. Ağırlık merkezi, her kenarortayı köşeden itibaren 2:1 oranında böler. Yani köşeden ağırlık merkezine olan uzaklık, ağırlık merkezinden kenar orta noktasına olan uzaklığın iki katıdır.
Dik üçgenlerde özel bir durum vardır: Hipotenüsün kenarortayı, hipotenüsün yarısına eşittir. Bu özellik, dik açının karşısındaki kenarın (hipotenüs) orta noktasından dik açının köşesine çizilen kenarortayın uzunluğunun, hipotenüsün yarısı olduğu anlamına gelir. Bu, çember içindeki dik üçgenlerle ilgili problemlerde sıkça kullanılır.
Ağırlık Merkezi Uygulamaları
Ağırlık merkezi, adından da anlaşılacağı gibi, bir üçgen levhanın denge noktasıdır. Eğer üçgen şeklinde kestiğiniz bir kartonu ağırlık merkezinden bir iğneye oturtursanız, karton dengede durur.
Köprü tasarımında ve yapı mühendisliğinde ağırlık merkezi çok önemlidir. Mühendisler, yük dağılımını hesaplarken üçgen yapıların ağırlık merkezlerini kullanarak hangi noktalara ne kadar yük bineceğini belirler. Örneğin, üçgen çatılarda kar yükünün nasıl dağılacağı, ağırlık merkezi hesaplarıyla belirlenir.
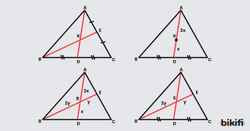
Bir üçgende ağırlık merkezini bulmak için 3 kenarortayın olması gerekmeyebilir. Aşağıdaki durumlarda da ağırlık merkezini bulduğumuzdan emin olabiliriz.
Üçgenin Kenar Orta Dikmeleri
Kenar orta dikme, bir kenarın orta noktasından o kenara dik olarak çizilen doğrudur. Her kenar için bir orta dikme vardır, yani bir üçgende üç kenar orta dikme bulunur.
Kenar Orta Dikme Tanımı
Kenar orta dikmelerin en önemli özelliği, üzerindeki her noktanın kenarın iki uç noktasına eşit uzaklıkta olmasıdır. Bu simetri özelliği sayesinde kenar orta dikmeler, üçgenin çevrel çemberinin merkezinde kesişir. Bu merkez O harfi ile gösterilir ve üçgenin üç köşesine de eşit uzaklıktadır.
Burada R, çevrel çemberin yarıçapıdır. Çevrel çember, üçgenin üç köşesinden de geçen çemberdir.
Üçgenin Yükseklikleri
Yükseklik, üçgenin bir köşesinden karşı kenara (veya karşı kenarın uzantısına) indirilen dik doğru parçasıdır. Her üçgende üç yükseklik vardır.
Yükseklik Tanımı ve Özellikleri
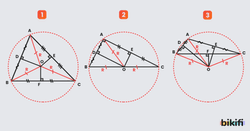
Yüksekliklerin kesişim noktasına diklik merkezi veya ortosantır denir ve H harfi ile gösterilir. Diklik merkezinin konumu, üçgenin türüne göre değişir:
- Dar açılı üçgende: H noktası üçgenin içindedir. Üç yükseklik de üçgenin içinde kesişir.
- Dik açılı üçgende: H noktası dik açının olduğu köşededir. Dik kenarlar zaten birbirlerine yüksekliktir.
- Geniş açılı üçgende: H noktası üçgenin dışındadır. Yüksekliklerin uzantıları üçgenin dışında kesişir.
Yükseklik Uygulamaları
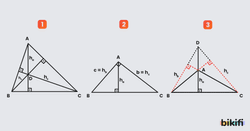
Yükseklikler, alan hesaplamalarında temel araçtır. Üçgenin alanı, herhangi bir kenar ile o kenara ait yüksekliğin çarpımının yarısına eşittir:
En kısa yol problemlerinde yükseklikler kullanılır. Bir noktadan bir doğruya gidilecek en kısa yol, o noktadan doğruya indirilen dikmedir (yükseklik). Bu prensip, yol yapımında, boru döşemede ve kablo çekmede maliyeti azaltmak için kullanılır.
Gölge yöntemiyle yön bulma da yükseklik prensibine dayanır. Güneşin konumuna göre bir çubuğun gölgesi, çubuğa dik açı yapar. Bu özellik kullanılarak pusula olmadan yön bulunabilir.
Yardımcı Elemanlar Arası İlişkiler
Üçgenin yardımcı elemanları, üçgenin türüne göre özel ilişkiler gösterir.
Özel Üçgenlerde Yardımcı Elemanlar
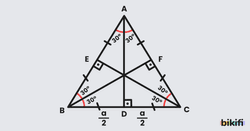
Eşkenar üçgende tüm simetri özellikleri bir aradadır. Açıortay, kenarortay, yükseklik ve kenar orta dikmelerin hepsi çakışıktır. Dolayısıyla ağırlık merkezi (G), diklik merkezi (H), iç teğet çember merkezi (I) ve çevrel çember merkezi (O) aynı noktadadır. Kenar uzunluğu a olan eşkenar üçgen için:
- Çevrel çember yarıçapı:
- İç teğet çember yarıçapı:
İkizkenar üçgende, tepe köşesinden (eşit kenarların birleştiği köşe) tabana indirilen açıortay, kenarortay, yükseklik ve kenar orta dikme çakışıktır. Bu doğru aynı zamanda üçgenin simetri eksenidir. Tüm özel noktalar (G, H, I, O) bu simetri ekseni üzerindedir.
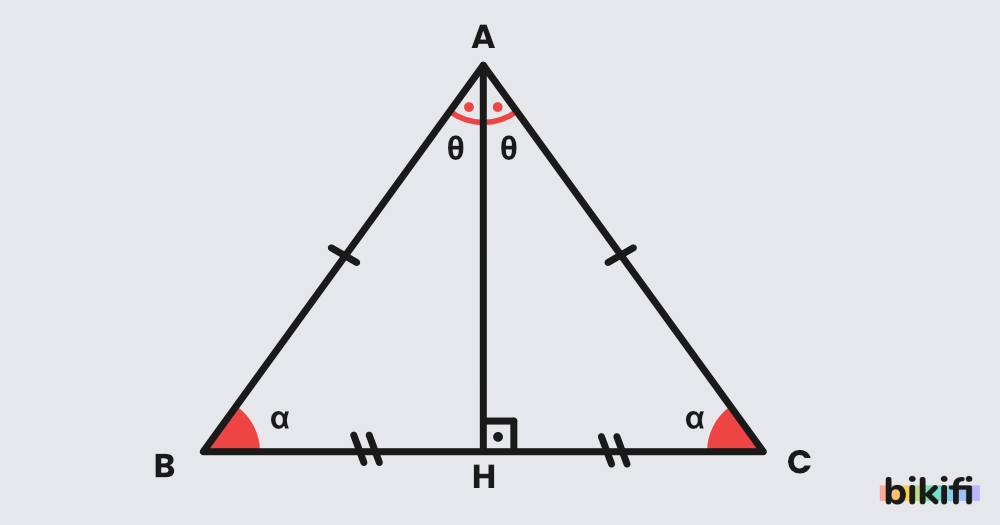
Dik üçgende ise hipotenüse ait kenarortayın özel bir özelliği vardır: Uzunluğu hipotenüsün yarısına eşittir. Bu özellik, dik üçgenin çevrel çemberinin merkezinin hipotenüsün orta noktasında olduğunu gösterir.
📚 Konuyla İlgili Terimler Özeti
- Açıortay (⭐⭐⭐): Bir açıyı iki eşit parçaya bölen ışın veya doğru parçası. Üçgende köşeden karşı kenara çizildiğinde, açıortay üzerindeki her nokta açının kollarına eşit uzaklıktadır. Günlük hayatta simetri gerektiren tasarımlarda kullanılır.
- Ağırlık Merkezi (⭐⭐⭐): Üçgenin kenarortaylarının kesişim noktası, G harfi ile gösterilir. Bu nokta, üçgen şeklindeki bir levhanın denge noktasıdır ve kenarortayları köşeden itibaren 2:1 oranında böler. Mühendislikte yük dağılımı hesaplarında kritik öneme sahiptir.
- Kenarortay (⭐⭐⭐): Üçgenin bir köşesinden karşı kenarın orta noktasına çizilen doğru parçası. Her üçgende üç kenarortay vardır ve bunlar ağırlık merkezinde kesişir. Yapı dengesi ve stabilite hesaplarında kullanılır.
- Yükseklik (⭐⭐⭐): Üçgenin bir köşesinden karşı kenara veya uzantısına indirilen dikme. Alan hesaplarının temelini oluşturur ve en kısa mesafe problemlerinde kullanılır.
- Kenar Orta Dikme (⭐⭐): Bir kenarın orta noktasından o kenara dik olarak çizilen doğru. Üzerindeki her nokta, kenarın uç noktalarına eşit uzaklıktadır.
- İç Teğet Çember (⭐⭐): Üçgenin içinde, her üç kenara da teğet olan çember. Merkezi, iç açıortayların kesişim noktasındadır.
- Çevrel Çember (⭐⭐): Üçgenin üç köşesinden de geçen çember. Merkezi, kenar orta dikmelerin kesişim noktasındadır.
- Dış Teğet Çember (⭐): Üçgenin bir kenarına ve diğer iki kenarın uzantılarına teğet olan çember. Her üçgende üç tane dış teğet çember vardır.
- Diklik Merkezi (⭐): Yüksekliklerin kesişim noktası, H harfi ile gösterilir. Konumu üçgenin türüne göre içerde, köşede veya dışarıda olabilir.