Geometrinin temel taşlarından biri olan üçgenler, günlük hayatımızda her yerde karşımıza çıkar. Çatıların eğiminden köprülerin yapısına, trafik levhalarından piramitlere kadar birçok yapıda üçgen formunu görürüz. Bu derste, üçgenlerin açıları ve kenarları arasındaki ilişkileri öğreneceğiz. Bu ilişkiler, mühendislikten mimarlığa, haritacılıktan bilgisayar grafiklerine kadar birçok alanda kullanılır.
Üçgende Açılar
Üçgen, düzlemde birleştirilmiş üç doğru parçasından oluşan geometrik şekildir. Her üçgenin üç köşesi ve bu köşelerde üç açısı vardır. Bu açıların özel özellikleri, matematikçilerin yüzyıllardır üzerinde çalıştığı konulardır.
Üçgenin İç Açılarının Ölçüleri Toplamı
Herhangi bir üçgen çizin – ister dar açılı, ister geniş açılı, isterse dik açılı olsun. Bu üçgenin köşelerindeki açıları ölçtüğünüzde şaşırtıcı bir gerçekle karşılaşırsınız: Üçgenin iç açılarının toplamı her zaman 180 derecedir.
Bu özellik, üçgenin en temel teoremlerinden biridir. Matematiksel olarak şöyle ifade ederiz:
Bu formülde A, B ve C üçgenin köşelerini, m(∠) ise açı ölçüsünü gösterir.
Paralel Doğrular Kullanarak İspat
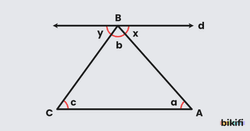
Bu teoremin ispatını anlamak için paralel doğrular kavramını kullanabiliriz:
- ABC üçgenini ele alalım
- B köşesinden AC kenarına paralel bir doğru çizelim
- Bu paralel doğru, A ve C köşelerindeki açılarla yöndeş açılar (aynı yöne bakan eş açılar) oluşturur
- B köşesinde oluşan düz açı 180 derecedir
- Bu düz açı, üçgenin üç iç açısının toplamına eşittir
Örnek Uygulama: Bir üçgenin iki açısı 45° ve 60° ise, üçüncü açı kaç derecedir?
Çözüm: 180° – 45° – 60° = 75°
Üçgenin Dış Açılarının Ölçüleri Toplamı
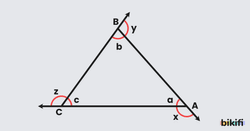
Dış açı (üçgenin bir kenarının uzantısı ile komşu kenar arasında kalan açı), üçgen geometrisinde önemli bir kavramdır. Her köşede bir dış açı oluşturulduğunda, bu üç dış açının toplamı her zaman 360 derece olur.
Bu özelliği anlamak için şunu düşünün: Her köşede iç açı ve dış açı birlikte 180 derece eder (çünkü düz açı oluştururlar). Üç köşe için:
- Toplam açı = 3 × 180° = 540°
- İç açılar toplamı = 180°
- Dış açılar toplamı = 540° – 180° = 360°
Üçgenin İç ve Dış Açılarının Ölçüleri Arasındaki İlişki
Üçgen geometrisinin en kullanışlı teoremlerinden biri dış açı teoremidir:
Bir dış açının ölçüsü, kendisine komşu olmayan iki iç açının toplamına eşittir.
Matematiksel ifadeyle:
Pratik Örnek: ABC üçgeninde A açısı 50°, B açısı 70° olsun. C köşesindeki dış açı kaç derecedir?
Çözüm: C’deki dış açı = A + B = 50° + 70° = 120°
Bu teorem, özellikle karmaşık geometrik şekillerde açı hesaplamalarını kolaylaştırır. Örneğin, bir binanın güneş panellerinin açısını ayarlarken veya uydu anteninin yönünü belirlerken bu ilişkiden yararlanılır.
Üçgende Açı ve Kenar İlişkileri
Üçgenlerde açılar ile kenarlar arasında doğrudan bir ilişki vardır. Bu ilişkiler, mühendislik hesaplamalarından günlük problem çözümlerine kadar birçok alanda kullanılır.
Açı-Kenar Büyüklük İlişkisi
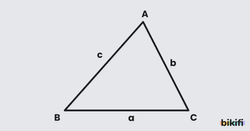
Üçgenlerde temel bir kural vardır: Büyük açının karşısında uzun kenar bulunur.
Bu ilişki şu şekilde çalışır:
- En büyük açının karşısında en uzun kenar
- En küçük açının karşısında en kısa kenar
- Orta büyüklükteki açının karşısında orta uzunlukta kenar bulunur
Günlük Hayat Örneği: Bir merdiven duvara yaslandığında, duvarla yaptığı açı ne kadar büyükse, merdivenin alt ucunun duvardan uzaklığı o kadar fazla olur.
Örnek olarak bize bilgisi verilirse bundan yola çıkarak c > a > b yorumunu yapabiliriz.
İkizkenar Üçgen Özellikleri
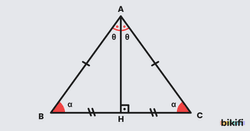
İkizkenar üçgen (iki kenarı eşit uzunlukta olan üçgen), özel özelliklere sahiptir:
- Eşit kenarların karşısındaki açılar (taban açıları) birbirine eşittir
- Tepe açısı (eşit kenarlar arasındaki açı) ile taban açıları arasında özel bir ilişki vardır
- Taban açılarının her biri = (180° – tepe açısı) ÷ 2
- ABC üçgeninde yan kenarlardır.
- taban açılarıdır.
- İkizkenar üçgende tabana ait yükseklik, hem açıortay hem de kenarortaydır.
- ise
Örnek: Bir ikizkenar üçgenin tepe açısı 40° ise, taban açıları kaç derecedir?
Çözüm: Her taban açısı = (180° – 40°) ÷ 2 = 70°
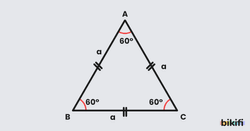
Eşkenar Üçgen Özellikleri
Eşkenar üçgen (tüm kenarları eşit uzunlukta olan üçgen), üçgenler arasında en simetrik olanıdır:
- Tüm açıları birbirine eşittir
- Her açı tam olarak 60 derecedir
- Eşkenar üçgen ikizkenar üçgenin özelliklerini sağlar.
Üçgen Eşitsizliği
Üçgen eşitsizliği, üç kenar uzunluğunun üçgen oluşturup oluşturamayacağını belirler:
İki kenarın toplamı, üçüncü kenardan her zaman büyük olmalıdır.
Matematiksel olarak, a, b ve c kenar uzunlukları için:
Bu formül şu anlama gelir:
- a kenarı, (b + c) toplamından küçük olmalı
- a kenarı, |b – c| farkından büyük olmalı
Üçgen Oluşturma Koşulları
Verilen üç uzunlukla üçgen oluşturulup oluşturulamayacağını kontrol etmek için üçgen eşitsizliğini kullanırız.
Örnek Problem: 3 cm, 4 cm ve 8 cm uzunluğundaki çubuklarla üçgen yapılabilir mi?
Kontrol edelim:
- 3 + 4 = 7, bu 8’den küçük ❌
- Bu uzunluklar üçgen oluşturamaz!
Başarılı Örnek: 5 cm, 7 cm ve 10 cm uzunlukları:
- 5 + 7 = 12 > 10 ✓
- 5 + 10 = 15 > 7 ✓
- 7 + 10 = 17 > 5 ✓
- Bu uzunluklar üçgen oluşturabilir!
Üçgen İçindeki Nokta Problemleri
Üçgenin içindeki herhangi bir noktadan köşelere çizilen doğru parçalarının toplamı, üçgenin çevresinden her zaman küçüktür.
Bu özellik, navigasyon sistemlerinde en kısa yol hesaplamalarında ve ağ bağlantılarının optimizasyonunda kullanılır.
Pratik Uygulamalar
Üçgen eşitsizliği günlük hayatta şu durumlarda karşımıza çıkar:
- GPS ve Harita Uygulamaları: İki nokta arasındaki en kısa mesafe hesaplamaları
- İnşaat ve Mimari: Çatı kirişlerinin uzunluklarının belirlenmesi
- Telekomünikasyon: Baz istasyonları arasındaki sinyal iletimi
- Spor: Futbolda pas üçgenleri, basketbolda pozisyon alma
Problem Çözme Stratejileri
Üçgen problemlerini çözerken şu sistematik yaklaşımı kullanabilirsiniz:
- Verilenlerİ Belirleyin: Hangi açılar ve kenarlar verilmiş?
- Kullanılacak Teoremi Seçin: İç açılar toplamı mı, dış açı teoremi mi, üçgen eşitsizliği mi?
- Adım Adım İlerleyin: Her adımı mantıksal olarak gerekçelendirin
- Sonucu Kontrol Edin: Bulduğunuz değerler mantıklı mı?
Geometrik İspat Yöntemleri
Geometride ispat, bir önermenin doğruluğunu mantıksal adımlarla gösterme sürecidir. Aksiyomlar (ispatı gerektirmeyen temel kabuller) ve teoremler kullanılarak yeni sonuçlara ulaşılır.
İspat Adımları ve Gerekçelendirme
Geometrik ispatlar genellikle tablo formatında organize edilir:
| Adım | İfade | Gerekçe |
|---|---|---|
| 1 | ABC bir üçgen | Verilen |
| 2 | m(∠A) + m(∠B) + m(∠C) = 180° | Üçgenin iç açılar�ı toplamı teoremi |
| 3 | m(∠A) = 60°, m(∠B) = 50° | Verilen |
| 4 | 60° + 50° + m(∠C) = 180° | 2 ve 3’ten yerine koyma |
| 5 | m(∠C) = 70° | 4’ten çözüm |
Her adımın mantıksal bir gerekçesi olmalıdır. Bu gerekçeler aksiyomlar, teoremler veya önceki adımlardan çıkarımlar olabilir.
Paralel Doğrular ve Açılar
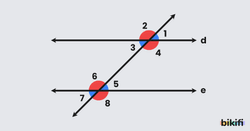
Paralel doğrular geometrik ispatlarda önemli araçlardır. İki paralel doğru bir kesenle kesildiğinde oluşan açı türleri:
- Ters Açılar: Kesişen iki doğrunun oluşturduğu açılardan karşılıklı duran açılara (komşu olmayanlara) ters açılar denir. 1 ile 3, 2 ile 4, 5 ile 7, 6 ile 8 ters açılardır ve ölçüleri birbirine eşittir. Bu durumun diğer adı “U kuralı” olarak geçer.
- İç Ters Açılar: Bir doğruyu kesen paralel doğruların iç kısmında kalan ve farklı yönlere bakan açılara iç ters açılar denir. 3 ile 5, 4 ile 6 iç ters açılardır ve ölçüleri birbirine eşittir. Bu durumun diğer adı “Z kuralı” olarak geçer. Z harfini oluşturan şekillerde aradaki açılar birbirine eşit oluyor ve biri için verilen açıyı direkt diğerine de yazabiliyoruz.
- Dış Ters Açılar: Bir doğruyu kesen paralel doğruların dış kısmında kalan ve farklı yönlere bakan açılara dış ters açılar denir. 1 ile 7, 2 ile 8 dış ters açılardır ve ölçüleri birbirine eşittir.
- Yöndeş Açılar: Açıyı oluşturan iki ışının her açı için aynı yöne baktığı açılara yöndeş açılar denir. 1 ile 5, 2 ile 6, 3 ile 7, 4 ile 8 yöndeş açılardır ve ölçüleri birbirine eşittir.
- Karşı Durumlu Açılar: Bir doğruyu kesen paralel doğruların iç kısımlarında kalan ve aynı yöne bakan açılara karşı durumlu açılar denir. 4 ile 5, 3 ile 6 karşı durumlu açılardır ve bu açıların ölçüleri toplamı her zaman 180 derecedir.
Bu açı ilişkileri, üçgenin iç açıları toplamının 180° olduğunu ispatlamak için kullanılır.
📚 Konuyla İlgili Terimler Özeti
- İç açı (⭐⭐⭐): Üçgenin içinde, iki kenarın oluşturduğu açıdır. Her üçgende üç iç açı bulunur ve toplamları 180 derecedir. Örneğin, bir çatının eğim açıları üçgenin iç açılarıdır.
- Dış açı (⭐⭐⭐): Üçgenin bir kenarının uzantısı ile komşu kenar arasında kalan açıdır. Bir binanın köşesinde dışarıya doğru açılan kapının açısı gibi düşünülebilir. Komşu olmayan iki iç açının toplamına eşittir.
- Üçgen eşitsizliği (⭐⭐⭐): Üçgenin herhangi iki kenarının toplamının üçüncü kenardan büyük olması kuralıdır. Bu kural, üç çubukla üçgen yapıp yapamayacağınızı belirler. Günlük hayatta, üç nokta arasındaki mesafeleri değerlendirirken kullanılır.
- İkizkenar üçgen (⭐⭐): İki kenarı eşit uzunlukta olan üçgendir. Eşit kenarların karşısındaki açılar da eşittir. Köprü ayakları ve çatı makasları genellikle ikizkenar üçgen formundadır.
- Eşkenar üçgen (⭐⭐): Üç kenarı da eşit uzunlukta olan üçgendir. Tüm açıları 60 derecedir. Trafik levhalarında ve doğal kristal yapılarında görülür.
- Tepe açısı (⭐⭐): İkizkenar üçgende eşit olan iki kenar arasındaki açıdır. Çatının en üst noktasındaki açı gibi düşünülebilir.
- Taban açısı (⭐⭐): İkizkenar üçgende tabanın (eşit olmayan kenarın) köşelerindeki açılardır. Bu iki açı birbirine eşittir.
- Açıortay (⭐): Bir açıyı iki eşit parçaya bölen doğru parçasıdır. Ayna yansımalarında kullanılan simetri ekseni gibidir.
- Komşu açılar (⭐): Ortak bir kenara sahip, yan yana bulunan açılardır. Bir köşede birleşen iki duvarın oluşturduğu açılar gibidir.
- Aksiyom (⭐): Matematikle doğruluğu kanıtlanmadan kabul edilen temel önermelerdir. “İki nokta arasındaki en kısa mesafe bir doğrudur” gibi.