Trigonometrik Fonksiyonların Açı Değerlerine Göre Sıralanması

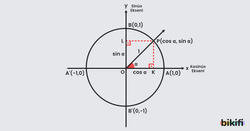
Öncelikle aşağıdaki görselde koordinat düzleminde bulunan birim çemberde sinüs ve kosinüs değerlerinin gösterimi görmekteyiz. Hipotenüs değeri 1 olduğu zaman karşı dik kenar yani y eksenindeki değer direkt bizim sinüs değerimizi, aynı şekilde komşu dik kenar olan x eksenindeki değer bize kosinüs değerimizi veriyor. Bu nedenle trigonometrik fonksiyonların açı değerlerine göre büyüklüklerinin nasıl değiştiğini nasıl sıralanacağını bulmak için birim çembere bakmak veya soru çözerken birim çemberi çizmemiz oldukça işimizi kolaylaştıracaktır. Aynı zamanda açı değerlerini trigonometrik fonksiyona göre işaretine dikkat ederek 0°-90° () arasına getirirsek büyüklükleri ve sıralamayı görmek için büyük kolaylık sağlayacak bir yöntem.

İlk olarak trigonometrik fonksiyonların büyüklüklerinin nasıl değiştiğini inceledikten sonra aralarında nasıl sıralama yapacağımızı ve örneklerini göreceğiz.

Sinüs Fonksiyonu Grafiği ve Değer İncelemesi

• İlk olarak sinüsle başlarsak birim çembere baktığımızda, açıya göre y ekseninde gördüğümüz değerin direkt o açının sinüs büyüklüğüne eşit olduğunu hatta bu nedenle y eksenine sinüs ekseni olduğunu biliyoruz.
• Açıyı sıfırdan başlatarak büyütmeye başladığımızda ilk başta y ekseninde gördüğümüz değer sıfır olacaktır.
• Sonrasında açımız büyüdükçe y eksenindeki değer yükselecektir. 1. bölgede yani 0°-90° () arasında açı büyüdükçe sinüs değeri artar.
• Aslında bu basit kısmı bilip trigonometrik fonksiyonların açı dönüşümlerini de bildiğiniz halde açı değerlerini 0°-90° () arasına çektiğimizde büyüklük sıralaması yapacak duruma gelirsiniz.
• Yine de buradan devam edecek olursak 2. bölgeye geçtiğimizde y ekseninde hala pozitif yerdeyiz fakat açı büyüdükçe y değerimiz azaldığı için 90°-180° () arasında açı büyüdükçe sinüs değeri azalır.
• İlk iki bölgeyi genel olarak incelediğimizde 90° ()’ye yaklaştığımızda sinüs değerinin arttığını görüyoruz.
• Diğer bölgelere geçtiğimizde o kısım tamamen negatif işaretli olacağı için büyüklük olarak yine ilk iki bölgeyi aynı şekil takip etse de sayısal değer olarak daha da aşağıda olacaktır.
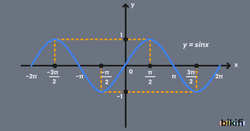
• Sinüsün bütün bölgelerdeki değerlerini bir arada görmek için aşağıdaki sinüs grafiğine bakabilirsiniz.

Sinüs (sin) Fonksiyonun Maksimum ve Minimum Değeri

Sinüs fonksiyonu 90°’de maksimum (+1), 270°’de minimum (-1) değerlerini alır. Negatif işareti düşünmeden, büyüklük olarak değerlendirirsek, 90° ve 270°’de maksimum büyüklükte (1 büyüklüğünde) değerleri alır diyebiliriz. Ancak işaretlerle birlikte düşünürsek:

• 90° (π/2)’de +1 (maksimum),
• 270° (3π/2)’de -1 (minimum) olur.

Kosinüs Fonksiyonu Grafiği ve Değer İncelemesi

Kosinüse geçtiğimizde ise birim çemberde açıya göre x ekseninde gördüğümüz değer direkt o açının kosinüs değerine eşit olduğunu biliyoruz. Yine açımızı sıfırdan başlatacak olursak x eksenine baktığımızda kosinüsün alabileceği en büyük değer olan 1’i göreceğiz. Açımız büyüdükçe x ekseninde gördüğümüz değer küçülecek ve 90° ()’ye geldiğimizde x eksenindeki yani kosinüs değeri sıfır olacak.

• 1. bölgede yani 0°-90° () arasında açı büyüdükçe kosinüs değeri azalır.
• 2. bölgede (90° – 180°) açı büyüdükçe kosinüs değerinin büyüklüğü artar (sıfırdan -1’e doğru azalır). Ancak negatif değerlerde olduğumuz için sayısal olarak (pozitif/negatif eksende sağa doğru) küçülecektir.
• Yani 90°’den 180°’e giderken kosinüs değerleri 0’dan -1’e kadar azalır.
• İlk iki bölgeye baktığımızda kosinüs değeri 0°’den başladığımızda maksimum noktadan en düşük noktasına kadar düşecektir.
• Sonra ise 180° (π) açısından itibaren bir yükselişe geçecek ve 360° (2π)’ye geldiğimizde yani 0° ‘de yine maksimum seviyeyi görecektir.
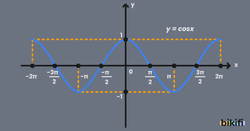
• Kosinüsün bütün bölgelerdeki değerlerini bir arada görmek için aşağıdaki kosinüs grafiğine bakabilirsiniz.

Kosinüs (cos) Fonksiyonun Maksimum ve Minimum Değeri

Kosinüs fonksiyonu, 0°’de maksimum (+1), 180°’de minimum (-1) değerlerini alır. Negatif işareti düşünmeden, büyüklük olarak değerlendirirsek, 0° ve 180°’de maksimum büyüklükte (1 büyüklüğünde) değerleri alır diyebiliriz. Ancak işaretlerle birlikte düşünürsek:

• 0° (0 radyan)’de +1 (maksimum),
• 180° (π radyan)’de -1 (minimum) olur.

Tanjant Fonksiyonu Grafiği ve Değer İncelemesi

Tanjant fonksiyonunda birim çemberdeki direkt bir eksene bakarak bulamıyoruz fakat sinüsü kosinüse bölerek veya karşı bölü komşu üzerinden iki ekseni baz alarak bulabiliriz. Yani sonuçta sinüs dediğimiz y eksenindeki değeri, kosinüs dediğimiz x eksenindeki değere bölerek bulacağız.

• Açı olarak sıfırdan başladığımızda y değerimiz 0, x değeri 1 olduğu için açılış 0 ile yapmış olduk.
• Sonrasında açıyı büyüttükçe y eksenindeki değer büyüyecek ve x eksenindeki değer küçülerek tanjant değerimiz büyümeye başlayacak.
• 90° ()’ye geldiğimizde y değeri 1, x değeri 0 olacağı için 1’i sıfıra böldüğümüz zaman sonucu sonsuz buluruz.
• Sonuç olarak 1. bölgede yani 0°-90° () arasında açı büyüdükçe tanjant değeri artar.
• Sonrasında 90° ()’yi geçtiğimizde ilk başlarda hala sonsuza yakın olacaktır fakat x ekseninde negatif değer olduğu için tanjant değerinin işareti eksi olacak ve en küçük değeri olan eksi sonsuzu alacaktır.
• 2. bölgede devam ettiğimizde açı büyüdükçe bu sefer x değeri negatif olsa bile büyüklük olarak artacak, y değeri azalacağı için 180° (π)’ye geldiğimizde tanjant değeri sıfır olacaktır.
• İlk iki bölgede olduğu gibi yeniden artacak ve 270° ()’de maksimumu görürken bölge değiştirdiğinde işaret de değişeceğinden minimumdan tekrar yükselecektir.
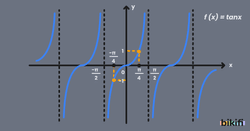
• Tanjantın bütün bölgelerdeki değerlerini bir arada görmek için aşağıdaki tanjant grafiğine bakabilirsiniz.

Tanjant (tan) Fonksiyonun Maksimum ve Minimum Değeri

Tanjant fonksiyonu, periyodik olarak tekrar eden ve belirli açılarda tanımsız hale gelen bir fonksiyondur. Bu nedenle, sinüs ve kosinüs gibi kesin maksimum veya minimum değerlerinden bahsetmek mümkün değildir. Ancak şunu söyleyebiliriz:

• Tanjant fonksiyonu 90° (π/2 radyan) ve 270° (3π/2 radyan) açılarında tanımsızdır ve bu açıların yakınlarında sonsuza gider.
• Tanjant fonksiyonunun belirli maksimum veya minimum değerleri yoktur çünkü pozitif ve negatif yönde sonsuza uzanır.

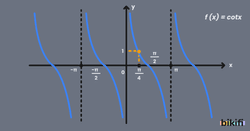
Kotanjant Fonksiyonu Grafiği ve Değer İncelemesi

Son olarak kotanjanta baktığımızda aynı tanjant gibi bir grafik bizi karşılayacak fakat tanjantın tam tersi olduğu için maksimum ve minimum noktalarında farklılık göreceğiz. Tanjantta sinüsü kosinüse böldüğümüz zaman sinüsün maksimum olduğu noktalarda tanjantın da o açılarda maksimum olduğunu gördük. Kontanjantta ise tam tersine kosinüs sinüse bölününce kosinüsün maksimum noktalarında kotanjant maksimum ve minimum noktalarını görecek. Yani tanjantla aynı bölgelerde aynı işaretli olacaktır.

• Kontanjant 0° açıda x değerinin 1, y değerinin 0 olmasıyla sonsuz değerini görürken açı büyüyüp 90° ()’ye yaklaştıkça bu değer sıfıra düşecektir.
• Buradan anladığımız 1. bölgede yani 0°-90° () arasında açı büyüdükçe kotanjant değeri azalır.
• Sonrasında negatif bölge olan 2. bölgeye geçtiğimizde kotanjant değeri negatif yönde büyür yani 2. bölgede yani 90°-180° () arasında açı büyüdükçe kotanjant değeri yine azalır.
• 180° (π)’de minimum nokta olan eksi sonsuza ulaşmış olacaktır ve oradan itibaren maksimum noktaya geçip tekrar azalmaya başlayacaktır.
• Bu anlattığımız kotanjantın değerlerini bütün bölgelerde bir arada görmek için aşağıdaki kotanjant grafiğine bakabilirsiniz.

Kotanjant (cot) Fonksiyonun Maksimum ve Minimum Değeri

Kotanjant fonksiyonu, tanjant fonksiyonu gibi periyodik olarak tekrar eden ve belirli açılarda tanımsız hale gelen bir fonksiyondur. Dolayısıyla sinüs ve kosinüs fonksiyonları gibi belirli maksimum veya minimum değerlerinden bahsedilemez. Ancak şunları söyleyebiliriz:

• Kotanjant fonksiyonu 0° (0 radyan), 180° (π radyan) gibi açılarda tanımsızdır ve bu açıların yakınlarında sonsuza gider.
• Kotanjant fonksiyonu da tanjant fonksiyonu gibi pozitif ve negatif yönde sonsuza doğru uzandığından belirli maksimum veya minimum değerlere sahip değildir.

Trigonometrik Fonksiyonların Sıralanması

Buraya kadar trigonometrik fonksiyonların bölgelere göre değerinin artıp azalmasını, işaretlerini ve grafiklerini gördük. Bundan sonrasında birbirleri ile nasıl büyüklüklerini kıyaslayacağımızı madde madde görelim.

• İlk olarak trigonometrik fonksiyonların işaretini belirleriz.
• Kıyaslama bakımından daha rahat etmek için açılarını 0°-90° () arasında bir değere getirecek şekilde dönüşüm yaparız.
• Artı işaretlileri ayrı, eksi işaretlileri ayrı sıralayacağız.
• Sinüs ve kosinüsü birbirine dönüştürerek kendi aralarında, tanjant ve kotanjantı birbirine dönüştürerek kendi aralarında büyüklük sıralaması yapabiliriz.
• Sinüs ve tanjant, kosinüs ve kotanjant gibi kıyaslama yapıldığında trigonometrik fonksiyonun o bölgedeki davranışına göre değişkenlik gösterir.
  • Örnek olarak 0°-90° () arasındaki açılar için konuşacak olursak aynı açıya sahip sinüs ve tanjant arasından tanjant daha büyük değere sahip olur çünkü tanjantta karşı dik kenar komşu dik kenara bölünürken sinüste daha büyük olan hipotenüse bölünecektir.
  • Sonuçta sinüs ve tanjant arasında aynı veya daha büyük bir açıya sahip olan tanjantın değeri sinüs değerinden büyük olur.
  • Bunun tam tersi durum da kosinüs ve kotanjant arasında olacaktır. Kosinüste x eksenine yaklaştıkça değeri büyüdüğü için kotanjant için de aynı durum geçerlidir hatta kosinüsten daha büyük olacaktır.
  • Yani kosinüs ve kotanjant arasında aynı veya daha küçük açıya sahip olan kotanjantın değeri kosinüs değerinden büyük olacaktır.
  • Bu bilgilere ek olarak sinüs ve kosinüs değerleri en fazla 1 olabilirken tanjant ve kotanjant değerleri 45° ()’de 1 değerini görürler. Tanjant 45° ()’den büyük(90° ()’a kadar), kotanjant 45° ()’den küçük(0° ‘a kadar) açılarda 1’den büyük olacakları için her türlü sinüs ve kosinüs değerlerinden büyük olacaklardır.
• İşareti artı olanlar zaten normal şekilde büyükten küçüğe doğru sıralanır fakat eksi işaretlileri ilk başta eksi işareti görmezden gelip büyükten küçüğe doğru sıralayıp sonrasında sıralamayı ters çevirebiliriz.
• En son artı ve eksi işaretlilerin sıralamasını birleştirerek sonuca ulaşırız.

Örnekler