Net Kuvvet
Bir cisme etkiyen kuvvetlerin toplanıp tek bir kuvvet olarak gösterilen haline net kuvvet denir ve olarak gösterilir. Her yön için farklı hesaplanır ve x yönündeki net kuvveti , yönündeki net kuvveti olarak gösterebiliriz.
Net kuvvet hesaplanırken dikkate alınması gereken dört kuvvet vardır:
Ağırlık: Bir cismin kütlesiyle bulunduğu ortamın yer çekimi ivmesinin çarpımından bulunan, yönü ise yere doğru( yönü) olan kuvvettir ve ile gösterilir.
Formül:
Tepki Kuvveti: Zeminin düz veya eğimli olması önemli olmaksızın üzerinde duran veya hareket eden cisimlere zemin tarafından uygulanan, yönü zemine dik olan kuvvettir ve ile gösterilir.
Gerilme Kuvveti: Bir cisim ip, halat, tel gibi malzemelerle bir yere bağlandığında cismi kendilerine doğru çektikleri kuvvettir ve ile gösterilir. Bu malzemelerin her yerindeki gerilme kuvveti aynıdır.
Sürtünme Kuvveti: Hareket eden veya ettirilmek istenen bir cisme zemin tarafından ters yönde uygulanan kuvvettir ve ile gösterilir. Duran cisme yönünde bir kuvvet uygulanıyorsa ve cisim hala hareket etmiyorsa –x yönünde aynı büyüklükte kuvvet uygulanıyordur ve buna statik sürtünme kuvveti denir. Sürtünme kuvvetinde bir eşik vardır ve siz o eşikten fazla kuvvet uygularsanız cisim harekete geçer fakat o eşik değeri kadar sürtünme kuvveti yine ters yönde etki etmeye devam eder. Bu sefer de hareketli olan cisme etkiyen sürtünme kuvvetine kinetik sürtünme kuvveti denir. Sürtünme kuvvetini cisme zeminden uygulanan tepki kuvveti ve zeminin sürtünme katsayısını çarparak bulabiliriz. Bulduğumuz bu değer yukarıda bahsettiğim eşik değerdir. Bu değerden küçük bir kuvvet etki ediyorsa cisim durur, büyük bir kuvvet etki ediyorsa cisim hareket eder.
Not: Sürtünme kuvveti hesaplandıktan sonra eğer cisme uygulanan F kuvveti bu değerden küçükse oluşan sürtünme kuvveti F kuvvetine eşittir. F kuvveti büyüdükçe sürtünme kuvvetinin değeri de büyüyecek ve maksimum seviyeye geldiğinde statik sürtünme kuvveti kinetik sürtünme kuvvetine dönüşecek ve cisim harekete geçecektir.
Kanunlar
Net kuvvet ve diğer kuvvetlerden bahsettikten sonra Newton’un hareket kanunlarından kısaca bahsedecek olursak;
I. Kanun(Eylemsizlik Prensibi): Tavana iple asılı bir cismi havada sabit tutan şey dengelenmiş kuvvetlerdir, yani cismin ağırlığının ipin gerilme kuvvetine eşit olup birbirlerini sıfırlamalarıdır. Net kuvvetin sıfır olması bir cismin duruyorsa durmaya devam etmesini, hareket ediyorsa sabit hızla hareketine devam etmesini sağlar. Cisimlerin bu gibi durumlarda konumu koruma eğilimine eylemsizlik prensibi denir.
II. Kanun(Dinamiğin Temel Prensibi): Tavana iple asılı cismin ipini kesersek artık yukarı doğru çeken gerilme kuvveti olmayacak ve net kuvvet sadece cismin ağırlığı olacaktır. Net kuvvet sıfırdan farklı olduğunda cisim o yönde ivmeli bir hareket yapar ve bu ivme cisme etki eden kuvvete ve cismin kütlesine göre değişir.
Formül:
III. Kanun(Etki-Tepki Prensibi): Bir cisim yerde hareketsiz duruyorsa net kuvvet sıfırdır. Bu cismin yere doğru bir ağırlık kuvveti vardır, bu yüzden net kuvveti sıfırlamak için yerden bu cismin ağırlığına eşit ve ters yönde bir kuvvet uygulanır. Cismin yere uyguladığı kuvvete etki kuvveti, yerin cisme uyguladığı kuvvete ise tepki kuvveti denir.
Formül:
Sürtünmesiz Düzlemde Serbest Cisim Diyagramı Net Kuvvetin Hesaplanması
Yatay Düzlem
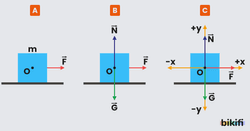
Sürtünmesiz yatay düzlemde kütleli bir cisme yatay F kuvveti uygulandığında serbest cisim diyagramı ve x-y koordinat sistemindeki gösterimi aşağıdaki gibi olur.
Cisme yatay yönde bir F kuvveti uygulandığından net kuvvet sıfırdan farklıdır ve cisim ivmeli hareket yapar. Cismin ivmesini formülü ile bulabiliriz. Düşeyde ise cismin ağırlığı kadar yerin tepki kuvveti vardır fakat zeminde sürtünme olmadığı için bir işimize yaramaz.
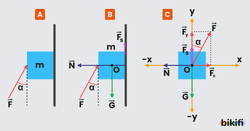
Düşey Düzlem
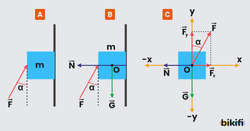
Sürtünmesiz düşey düzlemde kütleli bir cisme düşeyle açısı yapan F kuvveti uygulandığında serbest cisim diyagramı ve x-y koordinat sistemindeki gösterimi aşağıdaki gibi olur.
F kuvvetinin bileşenlerini aşağıdaki eşitliklerle hesaplayabiliriz.
Cismin hareketini yatayda incelersek düşey düzlemden kuvvetine karşın eşit büyüklükte bir N tepki kuvveti olacaktır ve net kuvvet sıfırdır.
Cismin hareketini düşeyde incelersek cismin ağırlığı ve arasında 3 farklı durum gözlemleyebiliriz.
- Cismin ağırlığı, kuvvetinden büyükse cisim aşağı doğru ivmeli hareket yapar ve ivmesi
eşitliğinden bulunabilir. - kuvveti, cismin ağırlığından büyükse cisim yukarı doğru ivmeli hareket yapar ve ivmesi
eşitliğinden bulunabilir. - Ağırlık ve kuvveti eşitse net kuvvet sıfır olur ve cisim hareketsiz kalır.
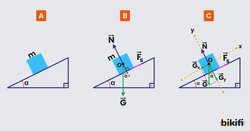
Eğik Düzlem
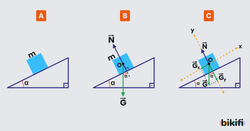
Yer çekimi ivmesinin olduğu eğim açısı olan sürtünmesiz eğik düzleme kütleli bir cisim bırakıldığında serbest cisim diyagramı ve x-y koordinat sistemindeki gösterimi aşağıdaki gibi olur.
Ağırlık bileşenlerini aşağıdaki eşitliklerle hesaplayabiliriz.
Cismin hareketini doğrultusunda incelersek kuvvetine zeminden N tepki kuvveti gelecektir ve net kuvvet sıfır olacaktır.
Cismin hareketini doğrultusunda incelersek kuvveti etki ettiğinden cisim aşağı doğru ivmeli hareket yapar ve ivmeyi aşağıdaki formüllerden bulabiliriz.
Yukarıda da görüldüğü gibi ivmesi cismin kütlesine bağlı değildir.
Sürtünmeli Düzlemde Serbest Cisim Diyagramı Net Kuvvetin Hesaplanması
Yatay Düzlem
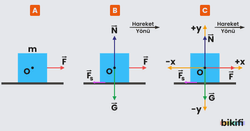
Sürtünmeli yatay düzlemde kütleli bir cisme yatay F kuvveti uygulandığında serbest cisim diyagramı ve x-y koordinat sistemindeki gösterimi aşağıdaki gibi olur.
Cismin hareketini düşeyde incelersek cismin ağırlığına eşit yukarı doğru bir N tepki kuvveti vardır. Bu durumda;
eşitliklerini yazabiliriz.
Cismin hareketini yatayda incelediğimizde F kuvvetiyle sürtünme kuvveti arasındaki ilişkiye göre 2 durum ortaya çıkar(aşağıdaki durumlar yukarıdaki sürtünme kuvveti bölümünde ayrıntılı biçimde anlatılmıştır).
- F kuvveti, sürtünme kuvvetinden küçük veya eşitse cisim hareketsiz kalır.
- F kuvvet, sürtünme kuvvetinden büyükse cisim ivmeli hareket yapar ve ivmesi aşağıdaki formüllerle bulunabilir.
Düşey Düzlem
Sürtünme katsayısı olan düşey düzlemde kütleli bir cisme düşeyle açısı yapan F kuvveti uygulandığında serbest cisim diyagramı ve x-y koordinat sistemindeki gösterimi aşağıdaki gibi olur.
Cismin hareketini yatayda incelediğimizde kuvvetine eşit büyüklükte ters yönde N tepki kuvveti uygulanır. Bu durumda;
eşitliklerini yazabiliriz.
Cismin hareketini düşeyde incelediğimizde ise ve kuvvetlerini toplayarak sürtünmesiz net kuvveti buluruz. Net kuvvet sıfır olursa cisim hareketsiz duracaktır. Net kuvvet sıfırdan farklıysa, yönü ne tarafa olursa zıt yönde sürtünme kuvveti etki edecektir. Net kuvvet, sürtünme kuvvetinden küçük veya eşitse yine cisim hareketsiz kalacaktır fakat sürtünme kuvvetinden büyükse cisim net kuvvet yönünde cisim ivmeli hareket yapacaktır. Cismin hareket ettiğini bulduktan sonra cisme sürtünme kuvveti de etki ettiği için net kuvvete dahil edilir. Cismin aşağı doğru ivmeli hareket yaptığını düşünürsek ivmesini aşağıdaki formüllerle bulabiliriz.
Eğik Düzlem
Sürtünme katsayısı k ve eğim açısı olan eğik düzleme m kütleli bir cisim bırakıldığında serbest cisim diyagramı ve x-y koordinat sistemindeki gösterimi aşağıdaki gibi olur.
Cismin hareketini y ekseninde incelediğimizde Gy kuvvetine eşit büyüklükte ters yönde N tepki kuvveti uygulanır. Bu durumda;
eşitliklerini yazabiliriz.
Cismin hareketini ekseninde incelediğimizde kuvveti sürtünme kuvvetinden küçük veya eşitse cisim hareketsiz kalır, sürtünme kuvvetinden büyükse cisim aşağı doğru ivmeli hareket yapacaktır. Cismin ivmesini aşağıdaki formüllerle hesaplayabiliriz.
Yukarıda görüldüğü gibi sürtünmeli eğik düzlemde de ivmesi cismin kütlesine bağlı değildir.
Birden Fazla Cismin Olduğu Durumlar
Üst üste, yan yana koyulan veya birbirine iple bağlanan cisimlere F kuvveti etki ettiğinde;
- Cisimler hareket etmiyorsa veya sabit hızla hareket ediyorsa net kuvvet sıfırdır ve her cisim için ayrı ayrı inceleme yaptığımızda üzerindeki bütün kuvvetlerin sıfır olması gerekir.
- Cisimler F kuvveti yönünde ivmeli hareket yapıyorsa bütün sistemin ivmesi ortaktır ve ivme hesaplanırken kütle yerine bütün cisimlerin kütlelerinin toplamı yazılır.
Sistemin ivmesi bulunduktan sonra her cisim için bu ivmeyi kullanıp kütlesiyle çarptığımızda o cisim üzerindeki net kuvveti bulabiliriz.