Logaritma Fonksiyonu

Bikifi Instagram'da

Logaritma’nın Okunuşu

Logaritma fonksiyonu üstel fonksiyonun ters fonksiyonudur. Örnek olarak bir y=log_ax logaritma fonksiyonunda a taban, y üstür ve a tabanında logaritma x diye okunur.

Logaritma ile Üstel Fonksiyon Arasındaki İlişki

Aşağıda bazı logaritmik ifadeler ve bunların üstel karşılıkları verilmiştir.

Bu İlişkinin Grafiksel Yorumu

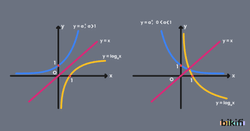
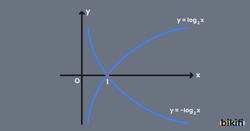
Logaritma fonksiyonunun grafiği üstel fonksiyonun grafiğinin y=x doğrusuna göre simetriğidir.

Aşağıda artan ve azalan üstel fonksiyon grafikleri ve bunların karşılığı olan logaritma fonksiyon grafikleri verilmiştir.

• Sol tarafta artan üstel fonksiyon grafiği ve aynı a>1 şartına sahip artan logaritma fonksiyonu grafiği,
• Sağ tarafta ise azalan üstel fonksiyon grafiği ve aynı 0<a<1 şartına sahip azalan logaritma fonksiyonu grafiği,

beraber verilmiştir.

Logaritma Fonksiyonunun En Geniş Tanım Kümesi

f(x)=log_g(x)h(x)

Yukarıdaki logaritmik fonksiyonun tanımlı olabilmesi için;

1. g(x)>0
2. g(x)1
3. h(x)>0

Şartlarını sağlıyor olmalıdır.

Logaritma Fonksiyonunun Grafiği

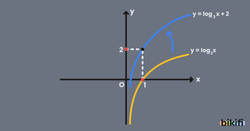
y=log_ax+k Fonksiyonunun Grafiği

y=log_ax+k fonksiyonunda k değişkenini artırmak veya azaltmak y üzerinde aynı etkiyi gösterecektir. Bu nedenle y=log_ax+k fonksiyon grafiğini çizmek istersek önce y=log_ax fonksiyonunun grafiğini çizeriz ve sonrasında k birim kadar y ekseninde yukarı veya aşağı kaydırırız.

Aşağıda örnek olarak y=log₃x+2 fonksiyonunun grafiği verilmiştir. Önce y=log₃x fonksiyonunun grafiği, ardından 2 birim yukarı ötelenmiş haliyle fonksiyonun grafiğine ulaşılmıştır.

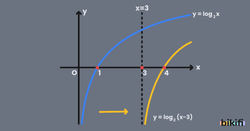
y=log_a(x+k) Fonksiyonunun Grafiği

y=log_a(x+k) fonksiyonunda k değişkeni direkt x değerinin alması gerektiği değeri etkilediği için grafiğe x ekseni yönünde etki eder. Bunun nedeni y=log_ax fonksiyonunda x’in yanına k değişkeni eklendiğinde x’in alması gereken değer bir k değişkeni kadar azalır. k pozitif bir sayıysa grafik x ekseninde negatif yöne, negatif bir sayıysa grafik x ekseninde pozitif yöne k birim kadar ötelenir.

Aşağıda örnek olarak y=log₂(x-3) fonksiyonunun grafiği verilmiştir. İlk olarak y=log₂x fonksiyonun grafiği verilmiş, sonrasında logaritmanın içi (x-3) olduğu için x alması gereken değerden hep 3 fazla olacağı için y=log₂x fonksiyonun grafiği 3 birim sağa kaymıştır.

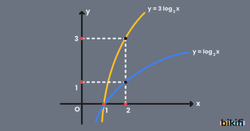
n>0, y=n.log_ax Fonksiyonunun Grafiği

y=n.log_ax fonksiyonunda y değeri her x değeri için n katına çıkacaktır. Bu fonksiyonun grafiği x değerlerinin aynı olup y değerlerinin değişmesi n sayısının değerine bağlı olarak y=log_ax grafiğine göre eğriliği değişmektedir.

Aşağıda bu duruma örnek olarak y=3log₂x fonksiyonunun grafiği verilmiştir. y=log₂x fonksiyonunda bulduğumuz her y değeri 3 ile çarpılırsa y=3log₂x fonksiyonunun grafiğine ulaşırız.

y=-log_ax Fonksiyonunun Grafiği

y=-log_ax fonksiyonundaki bütün y değerleri y=log_ax fonksiyonuna göre negatiftir. Bu nedenle y=-log_ax fonksiyonunun grafiği y=log_ax fonksiyonunun grafiğinin x eksenine göre simetriği alınmış halidir. Yani teknik olarak bütün y değerleri işaret değiştirmiş olur.

Aşağıda örnek olarak y=log₂x fonksiyonunun grafiği ve x eksenine göre simetriği alınmış hali olan y=-log₂x fonksiyonunun grafiği yer almaktadır.

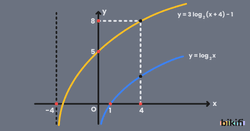
y=n.log_a(x±b)±c Fonksiyonunun Grafiği

y=n.log_a(x±b)±c fonksiyonunun grafiği şimdiye kadar öğrettiğimiz 3 yöntemin de sırayla uygulanarak bulunabilir. İlk olarak y=log_ax grafiği çizilir ve bu grafik x ekseni doğrultusunda b birim kadar sağa veya sola ötelenir. Sonrasında y değerleri n katına çıkarılarak eğriliği değişmiş yeni bir grafik elde ederiz. Son olarak ise y ekseni doğrultusunda c birim kadar yukarı veya aşağı ötelenerek y=n.log_a(x±b)±c fonksiyonunun grafiği elde edilir.

Aşağıda örnek olarak y=3log₂(x+4)-1 fonksiyonunun grafiği verilmiştir. İlk olarak y=log₂x fonksiyonunun grafiği çizilmiş ve yukarıdaki adımlar tek tek uygulanarak y=3log₂(x+4)-1 grafiği elde edilmiştir.

e Sayısı

Pek çok matematik ve mühendislik hesaplarında ifadesi geçer. Bu ifadede n sayısına 1’den başlayarak değerler verildiğinde bir süre sonra sonucun neredeyse aynı sadece virgülün çok sağında ihmal edilecek yerlerin değiştiği görülür. Bu çok tekrar eden sayıya e sayısı(Euler sayısı) adı verilmiştir ve hesaplamalarda direkt bu e sayısı kullanılmaktadır.

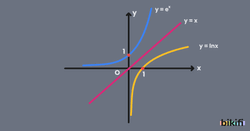
e sayısı e≅2,71828182845904523536… şeklinde devam eden irrasyonel bir sayıdır. y=e^x sayısının grafiği ise y=2^x ile y=3^x grafiğinin arasında yer almaktadır.

Doğal Logaritma Fonksiyonu

Tabanı e sayısı olan logaritma fonksiyonuna doğal logaritma fonksiyonu denir. Logaritmanın tabanı e sayısı olduğu zaman bunu ln şeklinde de ifade edebiliriz.

Aşağıda y=e^x fonksiyonunun grafiği ve ters fonksiyonu olduğu için y=x doğrusuna göre simetriği olan y=lnx fonksiyonunun grafiği verilmiştir.

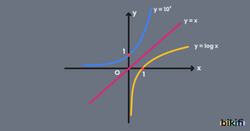
10 Tabanında Logaritma Fonksiyonu

Tabanı 10 olan logaritma fonksiyonuna 10 tabanında logaritma fonksiyonu (adi logaritma veya bayağı logaritma) denir. Logaritmanın tabanı 10 olduğunda tabanı yazmayabiliriz. Yani tabanında bir sayı yazmayan bir logaritmik ifade gördüğümüzde bunun 10 tabanında olduğunu anlarız.

Aşağıda y=10^x fonksiyonunun ve tersi y=logx fonksiyonunun grafikleri verilmiştir.

Logaritma Fonksiyonunun Özellikleri

log_a1=0

Logaritma fonksiyonunda tabanı ne olursa olsun logaritma 1’in sonucu her zaman sıfırdır. Bunun nedeni herhangi bir sayının sıfırıncı kuvveti her zaman 1’e eşittir.

log_aa=1

Logaritma fonksiyonundaki sayı ve tabanı eşit olan logaritmanın sonucu 1’dir. Fonksiyonun tersini almak için tabanı karşıya attığımızda logaritmadaki sayıyla eşit olması için tabanın üstüne sadece 1 gelebilir.

log_aa^x=x

Logaritma fonksiyonunda bulunan sayı, tabanın bir üslü ifadesiyse sonuç bu sayının üstü olur. Tabanı karşıya attığımızda eşitliğin sağlanması için karşı tarafın da logaritmadaki sayının üstüyle aynı olması gerekir.

log_axⁿ=n.log_ax

Logaritma fonksiyonundaki sayının üstü logaritmanın başına çarpım olarak atılabilir. Bu durumu açıklarken aşağıda da denklemleri takip edelim. İlk olarak tabanı karşıya atarak ters fonksiyona ulaşırız. Sonrasında her iki tarafın da üstünü n sayısıyla çarparız. Her iki tarafı da a tabanında logaritmada yazarak denklemin sol tarafında ulaşmak istediğimiz ifadeyi buluruz. Sağ taraftaki ifadeyi ise bir önceki özellikten faydalanarak logaritmadaki sayının üstüne eşit olduğunu buluruz. Böylelikle sonucumuz n ile çarpılmış halde çıktı.

a^log_ax=x

Bir sayının üstünde logaritmik bir ifade varsa ve tabanı bu sayıya eşitse sonuç direkt logaritmadaki sayıya eşit olur. Bunun nedeni üslü ifadenin tabanını karşı tarafa logaritma tabanı olarak atarsak sonuç üste verilen logaritmada bulunan sayıya eşittir.

log_a(x.y)=log_ax+log_ay

Çarpım durumunda bulunan sayıların logaritmaları, bu sayıların aynı logaritma tabanında ayrı ayrı yazılmış hallerinin toplamına eşittir. Açıklamak gerekirse çarpım durumundaki sayıların ayrı ayrı logaritmalarını alıp bunları m ve n harflerine eşitleyelim. Bu logaritmaların tersini aldığımızda çarpım durumundaki iki sayının da a cinsinden bir karşılığını buluruz. Bu sonuçları logaritmanın içine çarpım durumunda koyarak gerekli işlemleri yaptığımızda sonucu m+n, yani iki sayının da logaritmaları toplamını buluruz.

log_a(x/y)=log_ax-log_ay

Bölüm durumunda bulunan sayıların logaritmaları çarpım durumdan farklı olarak bu sayıların logaritmalarının toplamı değil bölenin logaritmasının bölüneninkinden çıkarıldığı duruma eşittir. Bölenin logaritmasını aldığımız zaman paydada bulunduğu için eksilisini alarak aynı şeyi elde edebiliriz.

log_ax=(log_cx/log_ca) ve log_ba=(1/log_ab) (Taban Değiştirme Özelliği)

Bir logaritma fonksiyonunda taban ve logaritması alınan sayıyı ayırıp ikisini de aynı tabanlı logaritmalarda bölerek tekrar yazabiliriz. İlk durumda taban olan sayının logaritması paydada olacaktır. Ayrıca bir logaritmada taban ve logaritması alınan sayının yerini değiştirmek istersek logaritmanın çarpmaya göre tersini almamız yeterli olacaktır. İlk durum için logaritmayı üslü ifade haline getirip her iki tarafı da istediğimiz bir tabanda logaritmaya alınca önceki özelliklerden de faydalanarak düzenlediğimizde sonuca ulaşırız.

Logaritmadaki sayıların yerlerini değiştirmek için hemen yukarıdaki özellikten faydalanabiliriz. Yeni belirlediğimiz tabanı üstekiyle aynı sayıyı seçersek yukarısı 1 olur ve aşağıdaki logaritmada sayılar tam tersi durumda olur.

log_aⁿb^m=(m/n).log_ab

Logaritma fonksiyonunda logaritması alınan sayının üstü çarpım olarak, tabanın üstü ise logaritmanın başına bölüm olarak geçer. Bunu açıklarken bir önceki özellikten yararlanarak önce logaritmadaki sayıyı ve tabanı herhangi bir taban belirleyerek ayırıp, sonrasında üstlerini başa çarpım olarak attığımız zaman aynı tabanlı logaritmaları bu sefer birleştiririz.

a^log_bc=c^log_ba

Bir sayının üstünde logaritmik ifade varsa bu sayıyla logaritması alınan sayının yerini değiştirebiliriz. Bu sonuca ulaşmak için öncelikle fonksiyonda üste bulunan logaritmadaki sayıyı taban kabul ederek her iki tarafı da logaritmaya alırız. Eskiden üst durumunda olan logaritmik ifade artık çarpım olarak diğer logaritmanın yanına gelir. Bu iki logaritmayı da aynı tabanda olacak şekilde ayırarak sadeleşebilecek duruma getirir ve düzenlersek a ve c sayılarının yerleşinin değişmiş haline ulaşırız.

log_x(1)x(2).log_x(2)x(3)…….log_x(n-1)x(n)=log_x(1)x(n)

Çarpım durumunda bulunan logaritmaların tabanları ve logaritması alınan sayı aynıysa direkt sadeleştirebilir, üslü ifadesiyse sadeleştirmenin sonucunda üstü çarpım olarak kalır. Bunun temeli taban değiştirme özelliğine dayanır. Bütün logaritmaları aynı tabanda yazdığımızda altlı üstlü aynı ifadelere denk geliriz ve bunları sadeleştirebiliriz.